3.10.1. Законы Кеплера
Для определения системы координат необходимо сначала определить
плоскость, затем в плоскости определить направление на
выделенную точку. Тогда с единичным вектором
![]() ,
направленным в эту точку, можно связать ось
,
направленным в эту точку, можно связать ось ![]() , с
перпендикуляром к плоскости -- единичный вектор
, с
перпендикуляром к плоскости -- единичный вектор
![]() и
ось
и
ось ![]() ; единичный вектор
; единичный вектор
![]() (ось
(ось ![]() системы координат)
определяется на основе векторного произведения так, чтобы
система осей была правой (
системы координат)
определяется на основе векторного произведения так, чтобы
система осей была правой (
![]() ).
).
Рассмотрим вопрос, как в пространстве определить эту плоскость и оси, лежащие в плоскости.
В основе динамического метода определения системы координат лежат
уравнения динамики -- и в первую очередь закон притяжения
Ньютона. Согласно этому закону два тела с массами ![]() и
и ![]() притягиваются с силой
притягиваются с силой
![]() , где
, где ![]() -- расстояние между
телами. Коэффициент
-- расстояние между
телами. Коэффициент
![]() называется постоянной
тяготения. Если тела расположены в точках
называется постоянной
тяготения. Если тела расположены в точках ![]() и
и ![]() с
декартовыми координатами
с
декартовыми координатами
![]() и
и
![]() ,
соответственно, то движение тела с массой
,
соответственно, то движение тела с массой ![]() описывается
уравнениями:
описывается
уравнениями:
точками обозначено дифференцирование по времени:
Введем обозначения:
![]() ,
,
![]() ,
,
![]() ,
,
![]() . Вычитая из уравнений (3.28)
уравнения (3.29), получим
. Вычитая из уравнений (3.28)
уравнения (3.29), получим
В уравнения (3.30-3.32) входят лишь относительные координаты двух точек, т.е. уравнения движения не зависят от положения начала системы координат. Умножая уравнение (3.30) на
Из (3.33) следует, что величина в скобках не зависит от времени, т.е.
Аналогичным образом из уравнений (3.31),(3.32) получим выражение:
а из (3.30) и (3.32):
Уравнения (3.34-3.36) называются интегралами площадей, а постоянные
Умножая уравнение (3.34) на ![]() , (3.35) -- на
, (3.35) -- на ![]() ,
(3.36) -- на
,
(3.36) -- на ![]() и складывая, находим, что
и складывая, находим, что
Уравнение (3.37) -- это уравнение плоскости. Значит, два тела, движущиеся в пространстве под действием силы притяжения, всегда находятся в одной и той же плоскости; траектория тела 2 относительно тела 1 является плоской кривой и называется орбитой. Другими словами орбита одного тела относительно другого лежит в плоскости.
Расположим оси ![]() системы координат, которую мы хотим
определить в плоскости орбиты, а ось
системы координат, которую мы хотим
определить в плоскости орбиты, а ось ![]() будет перпендикулярна
ей. Точку
будет перпендикулярна
ей. Точку ![]() (начало системы координат) совместим с телом с
массой
(начало системы координат) совместим с телом с
массой ![]() . Тогда уравнения движения (3.30-3.32) можно
записать в виде:
. Тогда уравнения движения (3.30-3.32) можно
записать в виде:
где
где
Умножим теперь уравнения (3.30-3.32) соответственно на
![]() ,
,
![]() ,
,
![]() и сложим. Координаты
и сложим. Координаты
![]() являются координатами тела 2 относительно тела 1.
В результате получим следующее уравнение:
являются координатами тела 2 относительно тела 1.
В результате получим следующее уравнение:
где
Так как орбита лежит в плоскости, и положение тела 2 относительно
тела 1 определяется лишь координатами ![]() , то удобно для
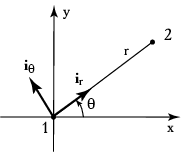
дальнейших вычислений ввести полярные координаты
, то удобно для
дальнейших вычислений ввести полярные координаты ![]() (рис. 3.12), так что
(рис. 3.12), так что
В полярной системе координат введем два единичных вектора
![]() , причем первый из них направлен
вдоль
, причем первый из них направлен
вдоль
![]() , а второй--перпендикулярен ему и
направлен в сторону увеличения угла
, а второй--перпендикулярен ему и
направлен в сторону увеличения угла ![]() . Тогда
. Тогда
или в векторном виде
Следовательно, в полярных координатах уравнение углового момента (3.39) имеет вид:
Допустим, что в момент ![]() тело 2 находилось на расстоянии
тело 2 находилось на расстоянии ![]() от
тела 1, а через промежуток времени
от
тела 1, а через промежуток времени ![]() переместилось на
угол
переместилось на
угол
![]() , причем расстояние стало равняться
, причем расстояние стало равняться
![]() . Считая, что промежуток времени
. Считая, что промежуток времени ![]() мал, можно считать
дугу, по которой движется тело 2, прямой линией. Тогда площадь
сектора, который образуют два радиус-вектора
мал, можно считать
дугу, по которой движется тело 2, прямой линией. Тогда площадь
сектора, который образуют два радиус-вектора ![]() и
и
![]() ,
будет близок к площади треугольника, равной
,
будет близок к площади треугольника, равной
![]() . Устремляя
. Устремляя
![]() к нулю и деля на промежуток времени
к нулю и деля на промежуток времени
![]() , находим, что площадь сектора, описываемая телом
равна
, находим, что площадь сектора, описываемая телом
равна
![]() . Следовательно, на
основе уравнения (3.42) можно утверждать, что за одинаковые
промежутки времени радиус-вектор описывает равные площади, причем
величина углового момента равна удвоенной площади сектора. Это
-- второй закон Кеплера.
. Следовательно, на
основе уравнения (3.42) можно утверждать, что за одинаковые
промежутки времени радиус-вектор описывает равные площади, причем
величина углового момента равна удвоенной площади сектора. Это
-- второй закон Кеплера.
Запишем теперь уравнение (3.38) в полярных координатах. Так как
производная
![]() уже найдена (3.41), то
уже найдена (3.41), то
Единичные векторы
Полагая, что
![]() , запишем уравнение (3.38)
в полярных координатах в следующем виде:
, запишем уравнение (3.38)
в полярных координатах в следующем виде:
Дифференциальные уравнения (3.42) и (3.44) описывают
зависимость расстояния ![]() одного тела относительно другого и угла
одного тела относительно другого и угла
![]() от времени. Для решения этих уравнений обычно исключают
время из (3.44) с помощью (3.42). Для удобства введем
параметр
от времени. Для решения этих уравнений обычно исключают
время из (3.44) с помощью (3.42). Для удобства введем
параметр ![]() , так что
, так что
Решение дифференциального уравнения второго порядка (3.45) записывается в виде:
Уравнение (3.46) является уравнением конических сечений. Вид
орбиты зависит от параметра ![]() -- эксцентриситета
орбиты. Если
-- эксцентриситета
орбиты. Если
![]() , то траектория
является эллипсом, если
, то траектория
является эллипсом, если ![]() , то
-- параболой, если
, то
-- параболой, если ![]() , то -- гиперболой. Вид орбиты можно
определить также по величине постоянной энергии в
уравнении (3.40), которая зависит от скорости и
радиуса-вектора тела. Поэтому удобно связать вид орбиты с
начальными параметрами
, то -- гиперболой. Вид орбиты можно
определить также по величине постоянной энергии в
уравнении (3.40), которая зависит от скорости и
радиуса-вектора тела. Поэтому удобно связать вид орбиты с
начальными параметрами ![]() и
и ![]() :
:
Ограничимся сейчас случаем, когда
![]() . В этом случае
уравнение (3.46) является математической формой
первого закона Кеплера.
. В этом случае
уравнение (3.46) является математической формой
первого закона Кеплера.
Если тело с массой ![]() назвать Солнцем, другое тело --
планетой, то первый закон Кеплера формулируется следующим
образом: планета движется по эллипсу, в одном из фокусов которого
находится Солнце. Параметр
назвать Солнцем, другое тело --
планетой, то первый закон Кеплера формулируется следующим
образом: планета движется по эллипсу, в одном из фокусов которого
находится Солнце. Параметр ![]() называется параметром эллипса и
связан с большой полуосью
называется параметром эллипса и
связан с большой полуосью ![]() эллипса
формулой:
эллипса
формулой:
![]() . Малая полуось
. Малая полуось ![]() может быть выражена через
может быть выражена через ![]() и
и ![]() :
:
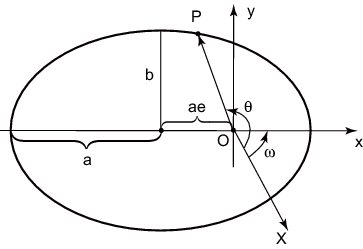
![]() (рис. 3.13). На рис. 3.13 Солнце находится в
точке
(рис. 3.13). На рис. 3.13 Солнце находится в
точке ![]() , планета -- в точке
, планета -- в точке ![]() , ось
, ось ![]() направлена в точку
восходящего узла орбиты, а ось
направлена в точку
восходящего узла орбиты, а ось ![]() -- в точку орбиты, ближайшей к Солнцу, которая называется
перигелием. Угол
-- в точку орбиты, ближайшей к Солнцу, которая называется
перигелием. Угол ![]() называется
долготой перигелия.
называется
долготой перигелия.
Если обозначить период обращения планеты ![]() как
как ![]() , то согласно
второму закону Кеплера за время
, то согласно
второму закону Кеплера за время ![]() планета опишет полный эллипс,
площадь которого равна
планета опишет полный эллипс,
площадь которого равна ![]() . Отношение площади эллипса к
периоду обращения равно половине углового момента планеты, т.е.
. Отношение площади эллипса к
периоду обращения равно половине углового момента планеты, т.е.
Так как

В случае, когда на тела 1 и 2 не действуют силы притяжения других тел (в небесной механике эта задача так и называется задачей двух тел), период обращения есть величина постоянная и может служить единицей времени. В начале XX века на основе наблюдений Солнца и Луны формировалась шкала эфемеридного времени (Ephemeris Time, ET). Так как из-за возмущений орбиты другими телами период обращения меняется, для построения шкалы ET необходимы были длительные наблюдения. Из-за сложности построения этой шкалы, а также из-за появления в середине 50-х годов XX века атомных стандартов частоты от шкалы времени, основанной на обращении Земли вокруг Солнца, пришлось отказаться. В настоящее время в основе счета времени лежит атомная шкала времени TAI, однако самой стабильной на больших интервалах времени может оказаться пульсарная шкала времени, причем пульсар является одной из звезд в двойной системе.
Обозначим через ![]() среднюю скорость движения планеты:
среднюю скорость движения планеты:
В небесной механике параметр
Аналогичное уравнение можно написать для другой планеты с массой
Уравнение (3.51) является математической записью третьего закона Кеплера. Так как для самой массивной планеты в солнечной системе -- Юпитера отношение
Квадраты периодов обращения планет относятся как кубы их больших полуосей. Определяя большую полуось
<< 3.10. Основы небесной механики | Оглавление | 3.10.2. Параметры и аномалии >>
|
Публикации с ключевыми словами:
астрометрия - сферическая астрономия - системы координат - шкалы времени
Публикации со словами: астрометрия - сферическая астрономия - системы координат - шкалы времени | |
См. также:
Все публикации на ту же тему >> | |