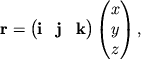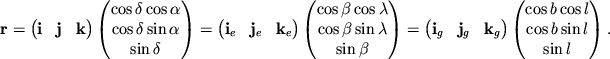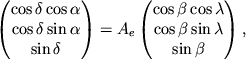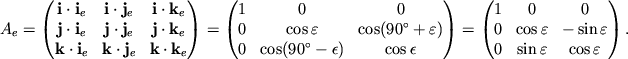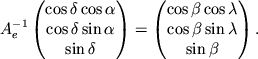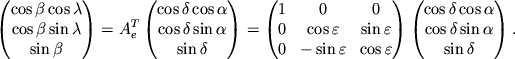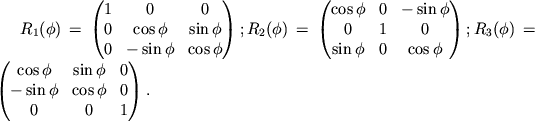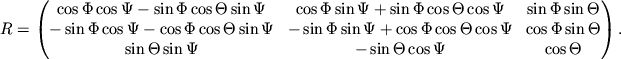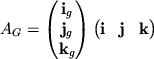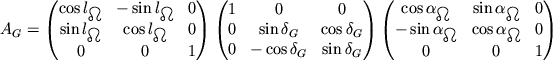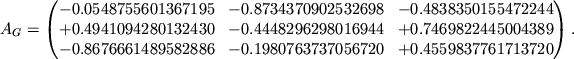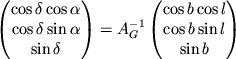3.5. Преобразование координат из одной системы в другую
Данная задача уже упоминалась при рассмотрении горизонтальной системы координат. Если система установки телескопа горизонтальная, то движение звезд в этой системе будет неравномерным. Для точного ведения телескопа за звездой требуется непрерывно пересчитывать экваториальные координаты звезды в горизонтальные.
Рассмотрим сначала классический метод и найдем выражения, связывающие экваториальные и горизонтальные координаты. Затем рассмотрим матричный метод, который значительно облегчает задачу преобразования координат вектора из одной системы в другую.
Рассмотрим треугольник ![]() (рис. 3.6).
(рис. 3.6).
По теореме синусов получим:
По теореме подобия получим:
Из системы уравнений (3.1-3.3) можно однозначно определить
Обратное преобразование (от ![]() и
и ![]() к
к ![]() и
и ![]() ) можно
записать в виде:
) можно
записать в виде:
Точно так же можно получить формулы, связывающие экваториальную систему координат с эклиптической, экваториальную с галактической и т.д.
Однако более просто найти преобразование от одной системы координат к другой системе с помощью матричных методов. Так как в дальнейшем мы будем использовать эти методы часто, рассмотрим их подробно.
Разложение вектора по тройке базисных векторов (![]() ,
, ![]() ,
,
![]() ) было записано в виде (2.5):
) было записано в виде (2.5):
где запись (
Разложим радиус-вектор одного и того же небесного объекта по
базисным тройкам экваториальной, эклиптической и галактической
систем. Для этого используем формулу (2.20), в которой
координаты
![]() заменяются на
заменяются на
![]() , или
, или
![]() , или
, или ![]() , и запишем матричное
равенство (3.5) в виде:
, и запишем матричное
равенство (3.5) в виде:
Чтобы найти преобразование от одной системы координат к другой, надо найти матрицу поворота от одной базисной тройки к другой. Например, найдем преобразование от экваториальной к эклиптической системе. Тогда
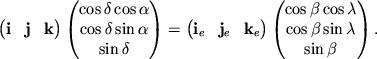
Умножим обе части уравнения на вектор-столбец
![]() слева, где индекс
"T" обозначает транспонирование, т.е.
слева, где индекс
"T" обозначает транспонирование, т.е.
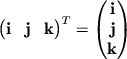 .
В результате получим
.
В результате получим
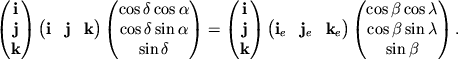
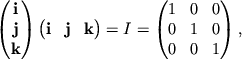
Таким образом преобразование от эклиптической к экваториальной системе можно записать следующим образом:
где
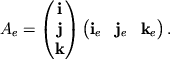
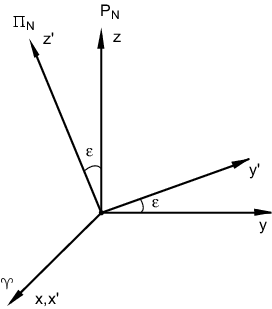
Вычислим матрицу ![]() в явном виде, используя рис. 3.7.
в явном виде, используя рис. 3.7.
Уравнения (3.7) и (3.8) однозначно определяют связь между двумя системами координат, и удобны при вычислении на компьютере. Тем не менее приведем преобразование (3.7) в явном виде:
Используя матричную запись (3.7) легко найти обратное преобразование от экваториальной к эклиптической системе координат. Для этого умножим уравнение (3.7) слева на матрицу, обратную
Матрица
Матрица ![]() описывает преобразование от экваториальной
системы к эклиптической. Вращение на угол
описывает преобразование от экваториальной
системы к эклиптической. Вращение на угол
![]() для
совмещения осей
для
совмещения осей ![]() и
и ![]() с осями
с осями ![]() и
и ![]() , соответственно,
называется правым, так как при этом движение воображаемого
правого винта совпадает с направлением оси
, соответственно,
называется правым, так как при этом движение воображаемого
правого винта совпадает с направлением оси ![]() . Матрица
. Матрица ![]() ,
поэтому, описывает правое вращение относительно оси
,
поэтому, описывает правое вращение относительно оси ![]() .
.
В явном виде из (3.13) получим:
Аналогично могут быть получены матрицы вращений относительно осей
![]() и
и ![]() . Для сохранения общности изложения обозначим матрицы
поворотов относительно осей
. Для сохранения общности изложения обозначим матрицы
поворотов относительно осей ![]() ,
, ![]() ,
, ![]() на угол
на угол ![]() как
как
![]() ,
, ![]() ,
, ![]() соответственно,
причем
соответственно,
причем
Матрица
С помощью матриц (3.15) можно вычислить любую матрицу, описывающую вращение в трехмерном пространстве.
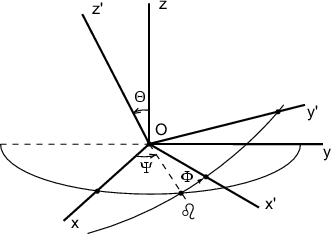
Рассмотрим две декартовы системы координат: ![]() и
и ![]() (рис. 3.8).
(рис. 3.8).
Углы ![]() ,
, ![]() ,
, ![]() называются углами
Эйлера. Три угла Эйлера однозначно
определяют поворот одной системы координат относительно другой. В
теоретической механике и астрономии эти углы имеют собственные
названия. Если оси
называются углами
Эйлера. Три угла Эйлера однозначно
определяют поворот одной системы координат относительно другой. В
теоретической механике и астрономии эти углы имеют собственные
названия. Если оси ![]() ,
, ![]() лежат в плоскости эклиптики, то
угол
лежат в плоскости эклиптики, то
угол ![]() называется углом прецессии. Угол
называется углом прецессии. Угол ![]() есть
угол нутации, а угол
есть
угол нутации, а угол ![]() называется углом
собственного вращения.
называется углом
собственного вращения.
Матрица вращения ![]() равна произведению трех матриц (обратите
внимание на порядок перемножения матриц и последовательность
вращений):
равна произведению трех матриц (обратите
внимание на порядок перемножения матриц и последовательность
вращений):
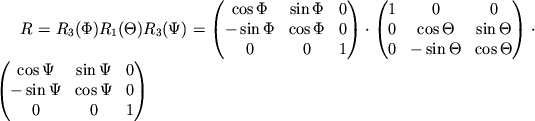
С помощью матричного метода легко найти матрицу преобразования
экваториальных координат (![]() ,
, ![]() ) в галактические
координаты (
) в галактические
координаты (![]() ,
,![]() ) (рис. 3.5).
) (рис. 3.5).
Из уравнения (3.6) имеем:
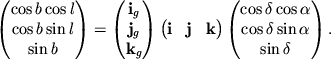
Матрица
является искомой матрицей преобразования.
Довольно трудно вычислить скалярные произведения
![]() ,
,
![]() и т.д.
непосредственно. Поэтому вычислим матрицу (3.17),
соответствующую переходу от экваториальной системы к
галактической следующим образом (см. рис. 3.5): выполним
первое вращение относительно оси мира на угол
и т.д.
непосредственно. Поэтому вычислим матрицу (3.17),
соответствующую переходу от экваториальной системы к
галактической следующим образом (см. рис. 3.5): выполним
первое вращение относительно оси мира на угол
![]() (прямое восхождение точки
(прямое восхождение точки ![]() ), т. е. вычисляем матрицу
), т. е. вычисляем матрицу
![]() , затем выполняем вращение относительно
линии узлов на угол
, затем выполняем вращение относительно
линии узлов на угол
![]() и вычисляем матрицу
и вычисляем матрицу
![]() , где
, где
![]() -- склонение северного галактического полюса. Третий поворот
-- это поворот относительно оси, соединяющей северный и южный
полюса Галактики, на угол
-- склонение северного галактического полюса. Третий поворот
-- это поворот относительно оси, соединяющей северный и южный
полюса Галактики, на угол
![]() . В результате матрица
. В результате матрица
![]() записывается в виде:
записывается в виде:
Подставив значения углов и вычислив произведение матриц, получим:
Обратное преобразование (от галактической к экваториальной системе координат) выражается матричным уравнением:
Так как матрица ![]() -- ортогональная, то
-- ортогональная, то
![]() .
.
В заключение используем матричный метод для вычисления матрицы
преобразования от горизонтальной (![]() ) к экваториальной системе
координат (
) к экваториальной системе
координат (![]() ) (рис. 3.3 и 3.6). Для этого
достаточно выполнить один поворот: относительно оси
) (рис. 3.3 и 3.6). Для этого
достаточно выполнить один поворот: относительно оси ![]() (обе
системы координат -- левые) на угол
(обе
системы координат -- левые) на угол
![]() , где
, где
![]() -- астрономическая широта. Следовательно матричное
уравнение преобразования координат можно записать как
-- астрономическая широта. Следовательно матричное
уравнение преобразования координат можно записать как
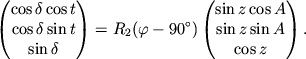 |
(3.23) |
Легко проверить, что эта система совпадает с уравнениями (3.4).
Используем полученные формулы преобразования координат для решения следующих задач.
Задача 1. Найти геометрическое место точек на небесной
сфере, у которых склонение ![]() равно эклиптической широте
равно эклиптической широте
![]() .
.
Решение. Преобразование координат точки из экваториальной в эклиптическую систему задается уравнениями (3.14):
Из первого уравнения получим:
![]() . Если
из второго уравнения выразить
. Если
из второго уравнения выразить
![]() и подставить в третье,
то найдем, что
и подставить в третье,
то найдем, что
![]() . Решением этой системы
будет
. Решением этой системы
будет
![]() .
.
Очевидно, что в точке весеннего равноденствия
![]() ,
также
,
также
![]() ; в точке осеннего равноденствия
; в точке осеннего равноденствия
![]() ,
,
![]() . Геометрическим
местом на сфере, удовлетворяющим условию
. Геометрическим
местом на сфере, удовлетворяющим условию
![]() (
(![]() -- некоторое число), является точка сферического
треугольника, одной из сторон которого является дуга между
полюсом мира и полюсом эклиптики и равная
-- некоторое число), является точка сферического
треугольника, одной из сторон которого является дуга между
полюсом мира и полюсом эклиптики и равная
![]() , двумя
другими -- дуги с длиной
, двумя
другими -- дуги с длиной
![]() . При увеличении
. При увеличении
![]() до
до ![]() треугольник вырождается в дугу, а точка
поднимается по дуге окружности, проходящей посередине между
полюсом мира и полюсом эклиптики.
треугольник вырождается в дугу, а точка
поднимается по дуге окружности, проходящей посередине между
полюсом мира и полюсом эклиптики.
Таким образом, геометрическим местом точек на небесной сфере
будет окружность -- пересечение большого круга, наклоненного к
экватору под углом
![]() и проходящего через
точки равноденствия, с небесной сферой.
и проходящего через
точки равноденствия, с небесной сферой.
Задача 2. Найти геометрическое место
точек на небесной сфере, у которых прямое восхождение ![]() равно эклиптической долготе
равно эклиптической долготе ![]() .
.
Решение. По аналогии с предыдущей задачей получим два уравнения:
которые удовлетворяются при
Задача 3. Каково прямое восхождение и склонение
северного и южного полюса эклиптики?
Решение. Координаты полюсов эклиптики можно найти, решая
уравнения (3.14). Однако проще найти решение, воспользовавшись
рис. 3.7. Для совмещения осей двух систем достаточно
повернуть экваториальную систему относительно оси ![]() на угол
на угол
![]() , т.е. полюсы эклиптики лежат в плоскости
, т.е. полюсы эклиптики лежат в плоскости ![]() .
Значит, координаты северного полюса эклиптики равны
.
Значит, координаты северного полюса эклиптики равны
![]() , а южного --
, а южного --
![]() .
.
Задача 4. В каких точках Земли эклиптика может
совпадать с первым вертикалом?
Решение. Напомним, что первым вертикалом называется
вертикальный круг, проходящий через точки востока и запада, т.е.
эклиптика должна проходить через зенит наблюдателя и точки
востока и запада. Значит северный полюс эклиптики должен
находиться в плоскости горизонта наблюдателя и совпадать с точкой
севера. Это возможно, если широта наблюдателя равна
![]() , т.е. наблюдатель находится северном тропике.
Солнце восходит в точке востока, движется через зенит наблюдателя
и заходит в точке запада. Если встать лицом к северу, то Солнце
встает справа, заходит слева.
, т.е. наблюдатель находится северном тропике.
Солнце восходит в точке востока, движется через зенит наблюдателя
и заходит в точке запада. Если встать лицом к северу, то Солнце
встает справа, заходит слева.
В южном полушарии аналогичная картина наблюдается, если
наблюдатель находится на южном тропике (широта равна
![]() ). Однако кажется, что небесная сфера вращается в
противоположную сторону; Солнце встает слева, заходит справа,
если встать лицом к югу.
). Однако кажется, что небесная сфера вращается в
противоположную сторону; Солнце встает слева, заходит справа,
если встать лицом к югу.
<< 3.4. Галактическая система координат | Оглавление | 3.6. Суточное вращение небесной >>
|
Публикации с ключевыми словами:
астрометрия - сферическая астрономия - системы координат - шкалы времени
Публикации со словами: астрометрия - сферическая астрономия - системы координат - шкалы времени | |
См. также:
Все публикации на ту же тему >> | |