Rambler's Top100Astronet    
  по текстам   по ключевым словам   в глоссарии   по сайтам   перевод   по каталогу 		 

На первую страницу << 2.2. Скаляры, векторы, тензоры | Оглавление | 2.4. Основные формулы сферической >>


2.3. Сферическая система координат

Для решения многих задач оказывается удобнее вместо декартовой системы использовать криволинейные системы координат. В общем случае используются три функции $ f_1(x,y,z)$, $ f_2(x,y,z)$, $ f_3(x,y,z)$ для определения положения тела в пространстве. Координатная сетка состоит из пересекающихся кривых $ f_i(x,y,z)=\textrm{const}, i=1,2,3$ вместо сетки прямых линий $ x=\textrm{const}, y=\textrm{const}, z=\textrm{const}$ в декартовой системе. Если функции выбраны подходящим образом, то положение объекта может быть однозначно определено с помощью криволинейных координат $ (f_1,f_2,f_3)$ вместо декартовых координат $ (x,y,z)$.

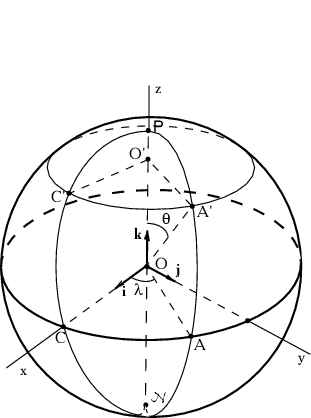
К таким системам относится и сферическая система координат, широко используемая не только в астрономии, но и других науках. Сферические координаты (см. рис. 2.5): $ r$ -- радиус-вектор объекта, $ \theta$ -- полярное расстояние, которое иногда называют коширотой, и $ \lambda$ -- долгота связаны с декартовыми координатами $ x,y,z$ уравнениями:

$\displaystyle x$ $\displaystyle =r\sin\theta \cos\lambda,$    
$\displaystyle y$ $\displaystyle =r\sin\theta \sin\lambda,$ (20)
$\displaystyle z$ $\displaystyle =r\cos\theta.$    

Полярное расстояние изменяется от $ 0^\circ$ до $ 180^\circ$, долгота -- от $ 0^\circ$ до $ 360^\circ$.

Рис. 2.5. Определение сферических координат точки

Система уравнений (2.20) представляет преобразование между сферической и декартовой системами координат. Следовательно, функции $ f_1,f_2,f_3$ равны:

$\displaystyle f_1$ $\displaystyle =r=\sqrt{x^2+y^2+z^2},$    
$\displaystyle f_2$ $\displaystyle =\theta=\textrm{arcctg}\frac{z}{\sqrt{x^2+y^2}}, \quad 0\leq\theta\leq\pi$    
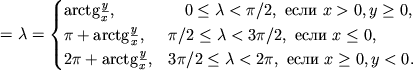$\displaystyle f_3$ $\displaystyle =\lambda=\begin{cases}\textrm{arctg}\frac{y}{x},& \quad 0\leq \lambda\lt \pi/2,\ \textrm{если}\ x\gt 0, y\geq 0, \\ \pi+\textrm{arctg}\frac{y}{x},& \pi/2\leq \lambda\lt 3\pi/2,\ \textrm{если}\ x\leq 0, \\ 2\pi+\textrm{arctg}\frac{y}{x},& 3\pi/2\leq \lambda\lt 2\pi,\ \textrm{если}\ x\geq 0, y\lt 0.\end{cases}$    

Вернемся к рис. 2.5. Через произвольно выбранные точки $ A$ и $ C$ проведем большой круг. Полюсы обозначим как $ P$ и $ \cal N$. Проведем теперь через полюсы и точку $ A$ большой круг (аналогично проведем большой круг через точку $ C$). Обозначим через $ \theta$ центральный угол между направлением на точку $ P$ и направлением на произвольную точку $ A'$, лежащую на сфере в плоскости большого круга $ PA\cal N$. Проведем через точку $ A'$ плоскость, параллельную большому кругу $ OAC$. Полученная плоскость является малым кругом, и радиус $ O'A'=\rho$ окружности равен, если $ OA'=R$:

$\displaystyle \rho=OA'\sin \theta = R\sin\theta.$ (2.21)

Введем декартову систему координат: ось $ x$ направим вдоль радиуса $ OC$, ось $ z$ -- вдоль радиуса $ OP$. Обозначим единичные векторы осей $ x$ и $ z$ как $ \bf i$ и $ \bf k$, соответственно. Направление оси $ y$ зададим единичным вектором $ \bf j$ согласно уравнению:

$\displaystyle {\bf j} ={\bf k}\times {\bf i}.$ (2.22)

Векторное произведение (2.22) векторов $ \bf k$ и $ \bf i$ определяет правую декартову систему координат $ Oxyz$.

Обозначим через $ \lambda$ двугранный угол между плоскостями $ PC\cal N$ и $ PA\cal N$. Числа $ R, \theta, \lambda$ называются сферическими координатами точки $ A'$. При $ R=1$ достаточно знать две координаты $ \theta, \lambda$ для определения положения точки на сфере. В следующей главе будут определены различные системы сферических координат. В каждой из них координаты $ \theta, \lambda$ имеют разные названия и могут обозначаться другими буквами.

Пусть точка $ C'$ лежит на сфере и является точкой пересечения большого круга $ PC\cal N$ и малого круга $ A'O'C'$ (рис. 2.5). Найдем длину дуги $ \widehat{A'C'}$. Так как центральный угол $ A'O'C'$ равен $ \lambda$, то

$\displaystyle \widehat{A'C'}=O'A'\cdot \lambda= R\lambda \sin\theta.$ (2.23)

Рассмотрим более подробно вопрос преобразования координат вектора в криволинейных координатах.

В криволинейной системе координат в отличие от декартовой возможны два способа выбора базисной тройки векторов: 1) базисные векторы являются касательными в точке $ (x_0, y_0, z_0)$ к кривым $ f_1(x_0, y=\textrm{const}, z=\textrm{const})$, $ f_2(x=\textrm{const}, y_0, z=\textrm{const})$, $ f_3(x=\textrm{const}, y=\textrm{const}, z_0)$; обозначим их как $ \mathbf{e}_1$, $ \mathbf{e}_2$, $ \mathbf{e}_3$ и 2) базисные векторы перпендикулярны в точке $ (x_0, y_0, z_0)$ к поверхностям, задаваемым функциями $ f_1,f_2,f_3$, т.е. $ f_1(x_0, y_0, z_0)=\textrm{const}$, $ f_2(x_0, y_0, z_0)=\textrm{const}$, $ f_3(x_0, y_0, z_0)=\textrm{const}$; обозначим их как $ \mathbf{e}^1$, $ \mathbf{e}^2$, $ \mathbf{e}^3$. Еще одним отличием от декартовой системы является то, что направление, а также длина базисных векторов может различаться в разных точках пространства.

В случае сферических координат поверхность, задаваемая уравнением $ f_1=\textrm{const}$, есть сфера радиуса $ r$, уравнение $ f_2=\theta=\textrm{const}$ определяет малый круг, а $ f_3=\lambda=\textrm{const}$ -- плоскость меридиана. Пересечения этих плоскостей со сферой являются окружностями. Так как кривые $ f_1(x_0, y=\textrm{const}, z=\textrm{const})$, $ f_2(x=\textrm{const}, y_0, z=\textrm{const})$, $ f_3(x=\textrm{const}, y=\textrm{const}, z_0)$ также являются окружностями, то в случае сферических координат обе базисные тройки совпадают. В общем случае это не так.

Два выбора базисных троек дают возможность найти проекции вектора $ \mathbf{a}$ как на оси $ \mathbf{e}_1$, $ \mathbf{e}_2$, $ \mathbf{e}_3$, так и на оси $ \mathbf{e}^1$, $ \mathbf{e}^2$, $ \mathbf{e}^3$:

$\displaystyle \mathbf{a}=a_1\mathbf{e}^1+a_2\mathbf{e}^2+a_3\mathbf{e}^3= a^1\mathbf{e}_1+a^2\mathbf{e}_2+a^3\mathbf{e}_3. $

Используя предложенное Эйнштейном правило суммирования, согласно которому в выражении суммирование выполняется по паре повторяющихся индексов (знак суммы при этом опускается), разложение вектора по базисным тройкам записывается в виде:

$\displaystyle \mathbf{a}=a_i\mathbf{e}^i,\quad \mathbf{a}= a^j\mathbf{e}_j;$ (2.24)

индексы суммирования могут обозначаться любыми буквами.

Числа $ a^1,a^2,a^3$ называются контравариантными, а $ a_1,a_2,a_3$ -- ковариантными проекциями вектора $ \mathbf{a}$.

Для базисных векторов $ {\mathbf{e}}_i, {\mathbf{e}}^k$ справедливы соотношения:

$\displaystyle {\mathbf{e}}_i\cdot {\mathbf{e}}^k= \delta^k_i=\begin{cases}1,& \textrm{при}\ i=k\\ 0,& \textrm{при}\ i\neq k. \end{cases}$ (2.25)

Символ $ \delta^k_i$ называется символом Кронекера2.2.

Скалярное произведение в криволинейных координатах записывается в виде

$\displaystyle {\mathbf{a}}\cdot{\mathbf{b}}= (a^i\mathbf{e}_i)\cdot(b_j\mathbf{e}^j)= (a^ib_j)\mathbf{e}_i\cdot\mathbf{e}^j. $

По определению $ \mathbf{e}_i\cdot\mathbf{e}^j=\delta_i^j$, причем $ \delta_i^i=1$, $ \delta_i^j=0$ при $ i\neq j$. Значит $ \mathbf{a}\cdot\mathbf{b}= (a^ib_j)\delta_i^j=a^ib_i$. Скалярное произведение можно вычислить, если известны ковариантные проекции вектора $ \mathbf{a}$ и контравариантные проекции вектора $ \mathbf{b}$, при этом $ \mathbf{a}\cdot\mathbf{b}=a^ib_i=a_ib^i$.

Для того, чтобы получить явное выражение ковариантных и контравариантных координат вектора, умножим скалярно первое из уравнений (2.24) на $ \mathbf{e}_j$, а второе -- на $ \mathbf{e}^i$. Учитывая определение (2.25), найдем:

$\displaystyle {\mathbf{a}}\cdot \mathbf{e}_j$ $\displaystyle =a_i(\mathbf{e}^i\cdot\mathbf{e}_j)= a_i\delta^i_j =a_j$    
$\displaystyle {\mathbf{a}}\cdot \mathbf{e}^i$ $\displaystyle =a^j(\mathbf{e}_j\cdot\mathbf{e}^i)= a^j\delta^i_j =a^i.$    

Значит,

$\displaystyle a_i ={\mathbf{a}}\cdot \mathbf{e}_i, \quad a^i={\mathbf{a}}\cdot \mathbf{e}^i.$ (2.26)

Используя формулы (2.26), перепишем (2.24) в виде:

$\displaystyle \mathbf{a}=({\mathbf{a}}\cdot \mathbf{e}_i)\mathbf{e}^i,\quad \mathbf{a}= ({\mathbf{a}}\cdot \mathbf{e}^i)\mathbf{e}_i.$ (2.27)

Соотношения справедливы для любого вектора $ \mathbf{a}$. Если вместо $ \mathbf{a}$ в (2.27) подставить базисные векторы, то получим:

$\displaystyle \mathbf{e}_k=(\mathbf{e}_k\cdot \mathbf{e}_i)\mathbf{e}^i,\quad \mathbf{e}^k= (\mathbf{e}^k\cdot \mathbf{e}^i)\mathbf{e}_i.$ (2.28)

Вводя обозначения

$\displaystyle g_{ki}=\mathbf{e}_k\cdot \mathbf{e}_i,\quad g^{ki}= \mathbf{e}^k\cdot \mathbf{e}^i,$ (2.29)

перепишем соотношения (2.28) таким образом:

$\displaystyle \mathbf{e}_k=g_{ki}\mathbf{e}^i,\quad \mathbf{e}^k= g^{ki}\mathbf{e}_i.$ (2.30)

Для построения базисной тройки $ \mathbf{e}_k$ по векторам $ \mathbf{e}^i$ необходимо знать матрицу с элементами $ [g_{ki}]$; и, наоборот, для построения базиса $ \mathbf{e}^k$ по базису $ \mathbf{e}_i$ -- матрицу с элементами $ [g^{ki}]$. Эти матрицы взаимно обратны, т.е.

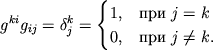
$\displaystyle g^{ki}g_{ij}= \delta^k_j=\begin{cases}1,& \textrm{при}\ j=k\\ 0,& \textrm{при}\ j\neq k. \end{cases}$

Величины $ g^{ki}$ и $ g_{ij}$ называются компонентами дважды контравариантного и ковариантного метрического тензора, соответственно.

Что из себя представляет тензор в математике? Как мы видели, задание базисной тройки определяет систему координат, в которой можно найти координаты произвольных векторов, т.е. их проекции на базисные векторы. Но так как при переходе в другую точку пространства направление и величина базисных векторов может меняться, то необходимо решить задачу о преобразовании проекций произвольных векторов из одной базисной тройки в другую. Эта задача решается методами тензорного анализа. Тензоры представляют собой систему величин, преобразующихся по линейному закону при переходе от одной системы координат к другой. Соотношения, записанные в тензорной форме, сохраняют свою форму в любой координатной системе.

Найдем теперь расстояние $ d{\mathbf{r}}$ между двумя бесконечно близкими точками пространства. Декартовы координаты вектора $ d{\mathbf{r}}$ равны $ dx, dy,dz$. Для этого, считая $ x,y,z$ в формулах (2.20) функциями переменных $ r,\theta,\lambda$ найдем дифференциалы $ dx$, $ dy$, $ dz$. По правилу вычисления дифференциалов функций многих переменных, сначала фиксируем переменные $ \theta, \lambda$ и находим изменение функции (частную производную $ \partial/\partial{r}$) в зависимости от приращения $ dr$, затем фиксируем переменные $ r$ и $ \lambda$ и находим изменение функции в зависимости от приращения $ d\theta$, и наконец при постоянных $ r$ и $ \theta$ находим частную производную $ \partial/\partial{\lambda}$. В результате получим:

$\displaystyle dx$ $\displaystyle =\frac{\partial{x}}{\partial{r}}dr+\frac{\partial{x}}{\partial{\theta}}d\theta +\frac{\partial{x}}{\partial{\lambda}}d\lambda,$    
$\displaystyle dy$ $\displaystyle =\frac{\partial{y}}{\partial{r}}dr+\frac{\partial{y}}{\partial{\theta}}d\theta +\frac{\partial{y}}{\partial{\lambda}}d\lambda,$ (31)
$\displaystyle dz$ $\displaystyle =\frac{\partial{z}}{\partial{r}}dr+\frac{\partial{z}}{\partial{\theta}}d\theta +\frac{\partial{z}}{\partial{\lambda}}d\lambda,$    

По определению частные производные $ \partial{x}/\partial{r},\partial{x}/\partial{\theta}$ и др. являются касательными к функциям $ x,y,z$, т.е. представляют собой компоненты базисных векторов $ \mathbf{e}_1$, $ \mathbf{e}_2$, $ \mathbf{e}_3$ вдоль направлений $ r,\theta,\lambda$:

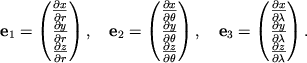
$\displaystyle \mathbf{e}_1=\begin{pmatrix}\frac{\partial{x}}{\partial{r}}\\ \frac{\partial{y}}{\partial{r}} \\ \frac{\partial{z}}{\partial{r}} \end{pmatrix}, \quad \mathbf{e}_2=\begin{pmatrix}\frac{\partial{x}}{\partial{\theta}}\\ \frac{\partial{y}}{\partial{\theta}} \\ \frac{\partial{z}}{\partial{\theta}} \end{pmatrix}, \quad \mathbf{e}_3=\begin{pmatrix}\frac{\partial{x}}{\partial{\lambda}}\\ \frac{\partial{y}}{\partial{\lambda}} \\ \frac{\partial{z}}{\partial{\lambda}} \end{pmatrix}. $

Это означает, что приращения $ dr,d\theta,d\lambda$ являются контравариантными проекциями вектора $ d{\mathbf{r}}$ в сферических координатах; уравнения (2.31), поэтому, представляют преобразование контравариантного вектора.

Следовательно, дифференциал функции является контравариантным вектором. Переобозначив бесконечно малые приращения как $ dx^1=dx$, $ dx^2=dy$, $ dx^3=dz$, найдем квадрат расстояния $ ds^2$ между двумя бесконечно близкими точками, который равняется в декартовой системе координат

$\displaystyle (ds)^2=(dx^1)^2+(dx^2)^2+(dx^3)^2.$ (2.32)

В более общем виде с учетом правила суммирования выражение для квадрата расстояния между двумя точками пространства записывается в виде:

$\displaystyle (ds)^2=(d{\mathbf{r}})^2=dx^idx^j({\mathbf{e}}_i\cdot{\mathbf{e}}_j)= g_{ij}dx^idx^j,$ (2.33)

где $ g$ -- метрический тензор. Закон вычисления расстояния (2.33) называется метрикой пространства.

Выбор той или иной системы координат дает возможность определить положение тела в пространстве и упростить уравнения движения тела, но не определяет свойства самого пространства. Задание метрики совместно с определением системы координат полностью описывает пространство. Это означает, что, зная метрический тензор, можно вычислить расстояние между двумя точками. В случае евклидова пространства, которое называется плоским, расстояние находится по формуле (2.32) и метрический тензор равен

$\displaystyle g=\begin{pmatrix}1&0&0\\ 0&1&0\\ 0&0&1 \end{pmatrix}.$ (2.34)

В случае плоского пространства метрический тензор $ g$ является диагональным и симметричным: $ g_{ij}=g_{ji}$. В общем случае тензор может иметь недиагональные элементы, которые зависят от координат, но тензор $ g$ всегда является симметричным, так как величины $ g_{ij}$ определяются из симметричной формы (2.33).

Если пространство не является плоским, то для вычисления расстояний уже нельзя использовать закон Пифагора (2.32). В частности, при вычислениях на сфере (в кривом пространстве) длина дуги между двумя точками не равна длине хорды (расстоянию в плоском пространстве).

Квадрат элемента длины в сферической системе координат легко найти, вычислив частные производные $ \partial{x}/\partial{r},\partial{x}/\partial{\theta}$ и т.д. и подставив их в (2.32). Используя уравнения (2.20), находим, что $ \partial{x}/\partial{r}=\sin\theta\cos\lambda$, $ \partial{x}/\partial{\theta}=r\cos\theta\cos\lambda$ и т.д. В результате после приведения подобных членов получим, что

$\displaystyle ds^2=dr^2+r^2d\theta^2+r^2\sin^2\theta d\lambda^2. $

Метрический тензор, следовательно, равен

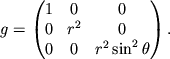
$\displaystyle g=\begin{pmatrix}1&0&0\\ 0&r^2&0\\ 0&0&r^2\sin^2\theta \end{pmatrix}. $

Тензор не содержит недиагональных членов. Это говорит о том, что сферические координаты ортогональны: сфера с радиусом $ r=\textrm{const}$, конус с углом $ \theta=\textrm{const}$ и меридиональная плоскость $ \lambda=\textrm{const}$ пересекаются под прямыми углами друг к другу.

Таким образом, свойства геометрии в криволинейной системе координат определяются компонентами $ g_{ij}$ метрического тензора. В дальнейшем мы будем рассматривать четырехмерное пространство-время для вычисления эффектов теории относительности (изменения хода часов, находящихся в гравитационном поле, отклонения луча света). В четырехмерном пространстве-времени имеется, следовательно, 16 компонент тензора, из них только 10 различны из-за симметричности тензора (четыре с одинаковыми индексами и $ 12/2=6$ с различными индексами).


<< 2.2. Скаляры, векторы, тензоры | Оглавление | 2.4. Основные формулы сферической >>

Публикации с ключевыми словами: астрометрия - сферическая астрономия - системы координат - шкалы времени
Публикации со словами: астрометрия - сферическая астрономия - системы координат - шкалы времени
См. также:
Все публикации на ту же тему >>

Мнения читателей [13]
Оценка: 3.5 [голосов: 304]
 
О рейтинге
Версия для печати Распечатать

Астрометрия - Астрономические инструменты - Астрономическое образование - Астрофизика - История астрономии - Космонавтика, исследование космоса - Любительская астрономия - Планеты и Солнечная система - Солнце

Астронет | Научная сеть | ГАИШ МГУ | Поиск по МГУ | О проекте | Авторам

Комментарии, вопросы? Пишите: info@astronet.ru или сюда

Rambler's Top100 Яндекс цитирования