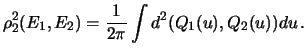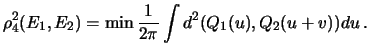Топология и метрика пар кеплеровских орбит
<< 3. Топология пар орбит | Оглавление | 5. Почти пересекающиеся орбиты >>
4. Естественные метрики в пространстве кеплеровских орбит
Будем теперь считать ![]() точкой в пятимерном пространстве
точкой в пятимерном пространстве ![]() кеплеровских эллипсов. Построим несколько естественных метрик
кеплеровских эллипсов. Построим несколько естественных метрик
![]() в
в ![]() . Малость
. Малость ![]() означает, что орбиты
означает, что орбиты
![]() почти совпадают.
почти совпадают.
Для построения расстояния представляется естественным сравнивать точки с одинаковой эксцентрической аномалией. Таким путем получаем равномерную и среднеквадратическую метрики
Наибольшее значение и интеграл берутся по отрезку
Легко доказать, что все аксиомы метрического пространства выполнены
для обеих метрик (10), (11), если исключить круговые
орбиты. Иными словами, расстояния (10), (11) определены и
топологически эквивалентны в пространстве ![]() некруговых
эллиптических орбит. Они разрывны в окрестности хотя бы одной
круговой орбиты из пары. Причина очевидна. Например, две компланарные
орбиты с одинаковой большой полуосью и почти нулевыми
эксцентриситетами почти совпадают независимо от направления апсид. Но
оба расстояния существенно зависят от их направления.
некруговых
эллиптических орбит. Они разрывны в окрестности хотя бы одной
круговой орбиты из пары. Причина очевидна. Например, две компланарные
орбиты с одинаковой большой полуосью и почти нулевыми
эксцентриситетами почти совпадают независимо от направления апсид. Но
оба расстояния существенно зависят от их направления.
Чтобы избежать неприятностей, мы должны сравнивать точки, имеющие различные взаимные положения. Хороший способ - ввести следующие метрики:
Наибольшее значение и интеграл берутся по отрезку
Все аксиомы метрического пространства выполнены
для обеих метрик (12), (13) во всем пространстве ![]() ,
хотя доказательство много сложнее, чем в предыдущем случае.
Расстояния (12), (13) топологически эквивалентны и превращают
,
хотя доказательство много сложнее, чем в предыдущем случае.
Расстояния (12), (13) топологически эквивалентны и превращают
![]() в открытое, неограниченное, локально-компактное метрическое
пространство.
в открытое, неограниченное, локально-компактное метрическое
пространство.
Приведем алгоритмы определения расстояний ![]() .
.
1. Обозначим
![]() . Очевидно,
. Очевидно,
где
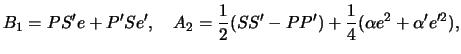
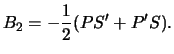
Первый шаг состоит в нахождении всех вещественных, лежащих на
окружности ![]() корней уравнения
корней уравнения
где
2. Интеграл (11) элементарен. Для второго расстояния получаем простую формулу
3. Алгоритм вычисления третьего расстояния столь сложен,
что мы не рекомендуем использовать ![]() на практике.
на практике.
4. Интеграл в (13) элементарен
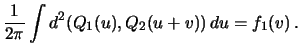
<< 3. Топология пар орбит | Оглавление | 5. Почти пересекающиеся орбиты >>
|
Публикации с ключевыми словами:
Небесная механика - кеплеровы орбиты
Публикации со словами: Небесная механика - кеплеровы орбиты | |
См. также:
Все публикации на ту же тему >> | |