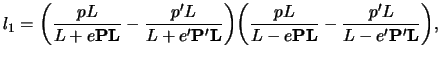Топология и метрика пар кеплеровских орбит
<< 2. Евклидово расстояние между орбитами | Оглавление | 4. Естественные метрики в ... >>
3. Топологическое расположение пар кеплеровских орбит
в
пространстве
Пара эллипсов общего положения может быть вложена в трехмерное
пространство двумя топологически различными способами. Они могут быть
сцеплены (случай ![]() ) и нет (случай
) и нет (случай ![]() ). Вырожденный случай
пересечения
). Вырожденный случай
пересечения ![]() разделяет
разделяет ![]() и
и ![]() .
Алгебраическая топология оперирует с коэффициентом зацепления
.
Алгебраическая топология оперирует с коэффициентом зацепления
![]() , определенным на каждой паре топологических
окружностей и равным
, определенным на каждой паре топологических
окружностей и равным ![]() в случаях
в случаях ![]() соответственно.
соответственно.
На практике эта разрывная функция неудобна. Для некомпланарных орбит
мы предлагаем простой непрерывный аналог ![]() величины
величины ![]() ,
отрицательный, положительный и равный нулю в вышеперечисленных случаях
и несущий дополнительные сведения о расстоянии между орбитами. Для
близких к пересечению орбит
,
отрицательный, положительный и равный нулю в вышеперечисленных случаях
и несущий дополнительные сведения о расстоянии между орбитами. Для
близких к пересечению орбит ![]() мало.
Т.к. критерий
мало.
Т.к. критерий ![]() не годится в компланарном случае, мы вводим также
два дополнительных критерия
не годится в компланарном случае, мы вводим также
два дополнительных критерия ![]() и
и ![]() .
.
1. Пространственный случай. Пусть орбиты ![]() некомпланарны. Тогда
вектор
некомпланарны. Тогда
вектор
![]() параллелен линии взаимных узлов и
параллелен линии взаимных узлов и
![]() . Очевидно,
. Очевидно,
Радиусы
Он не зависит от координатной системы. Кроме того,
где
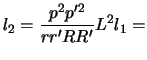
В случае
2. Компланарный случай. Если взаимный наклон равен нулю, то
![]() не определен, а
не определен, а ![]() равен нулю. Мы не можем различить случаи
равен нулю. Мы не можем различить случаи
![]() и
и ![]() (случай
(случай ![]() не встречается в двумерном пространстве).
Чтобы заполнить лакуну, введем третий коэффициент
не встречается в двумерном пространстве).
Чтобы заполнить лакуну, введем третий коэффициент
имеющий смысл только в компланарном случае.
Именно, ![]() , если
, если ![]() ,
, ![]() не пересекаются (случай
не пересекаются (случай ![]() );
);
![]() - в противоположном случае
- в противоположном случае ![]() . Точнее,
. Точнее,
![]() отвечает трансверсальному пересечению в двух точках;
отвечает трансверсальному пересечению в двух точках;
![]() отвечает единственной общей точке, в которой
отвечает единственной общей точке, в которой ![]() ,
, ![]() касаются друг друга, или наиболее вырожденному случаю
касаются друг друга, или наиболее вырожденному случаю ![]() . Стоит
заметить, что
. Стоит
заметить, что ![]() непрерывен на множестве пар компланарных
эллипсов.
непрерывен на множестве пар компланарных
эллипсов.
Из свойств ![]() можно попутно вывести заключение о числе
точек пересечения кеплеровских орбит
можно попутно вывести заключение о числе
точек пересечения кеплеровских орбит ![]() .
.
Существует пять и только пять вариантов:
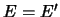 .
.
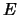 и
и 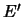 имеют общую часть, хотя
имеют общую часть, хотя 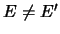 . Это возможно
только в случае двух прямолинейных орбит.
. Это возможно
только в случае двух прямолинейных орбит.
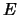 и
и 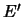 имеют ровно две общие точки, в обоих пересечение
трансверсально.
имеют ровно две общие точки, в обоих пересечение
трансверсально.
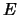 и
и 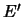 имеют ровно одну общую точку, в которой
имеют ровно одну общую точку, в которой 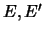 трансверсально пересекаются или касаются. В последнем случае они
лежат в одной плоскости и одна из них лежит внутри другой.
трансверсально пересекаются или касаются. В последнем случае они
лежат в одной плоскости и одна из них лежит внутри другой.
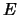 и
и 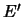 не имеют общих точек.
не имеют общих точек.
<< 2. Евклидово расстояние между орбитами | Оглавление | 4. Естественные метрики в ... >>
|
Публикации с ключевыми словами:
Небесная механика - кеплеровы орбиты
Публикации со словами: Небесная механика - кеплеровы орбиты | |
См. также:
Все публикации на ту же тему >> | |