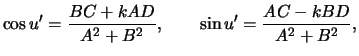Топология и метрика пар кеплеровских орбит
<< 1. Введение | Оглавление | 3. Топология пар орбит >>
2. Евклидово расстояние между двумя кеплеровскими орбитами
Обозначим через ![]() кеплеровский эллипс, рассматриваемый как
множество точек в
кеплеровский эллипс, рассматриваемый как
множество точек в ![]() . Пусть
. Пусть ![]() - евклидово
расстояние между двумя орбитами, т.е. наименьшее значение расстояния
- евклидово
расстояние между двумя орбитами, т.е. наименьшее значение расстояния
![]() между парами точек, лежащих на соответствующих эллипсах.
С XIX столетия опубликованы сотни работ, посвященных определению
между парами точек, лежащих на соответствующих эллипсах.
С XIX столетия опубликованы сотни работ, посвященных определению
![]() различными приближенными способами. Альтернативный подход состоит
в сведении задачи к решению уравнения
различными приближенными способами. Альтернативный подход состоит
в сведении задачи к решению уравнения
Мы построили алгоритм наименьшей сложности для определения ![]() .
Именно, построили играющий роль
.
Именно, построили играющий роль ![]() тригонометрический многочлен
восьмой степени
тригонометрический многочлен
восьмой степени ![]() от эксцентрической аномалии
от эксцентрической аномалии ![]() . В общем случае
тригонометрического многочлена меньшей степени не существует.
В вырожденных случаях мы построили тригонометрические многочлены
меньшей степени, а в случае двойного и тройного вырождения получили
явное решение для
. В общем случае
тригонометрического многочлена меньшей степени не существует.
В вырожденных случаях мы построили тригонометрические многочлены
меньшей степени, а в случае двойного и тройного вырождения получили
явное решение для ![]() . Подробное решение задачи (с пропуском одного из
вырожденных случаев) содержится в
[1]. Здесь мы приведем основные результаты.
. Подробное решение задачи (с пропуском одного из
вырожденных случаев) содержится в
[1]. Здесь мы приведем основные результаты.
Пусть
![]() - кеплеровские элементы
- кеплеровские элементы ![]() ;
;
![]() . Описывающие
. Описывающие ![]() величины помечаются штрихом. Вектор
положения
величины помечаются штрихом. Вектор
положения ![]() на
на ![]() выразим через эксцентрическую аномалию
выразим через эксцентрическую аномалию ![]()
Здесь
Здесь
Для приведенного к безразмерному виду квадрата функции расстояния
![]() легко вывести представление
легко вывести представление
Здесь
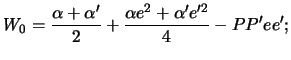
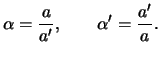
Функция (2) является тригонометрическим многочленом двух
переменных ![]() и принимает наименьшее на двумерном торе значение
в одной из критических точек, удовлетворяющих уравнениям
и принимает наименьшее на двумерном торе значение
в одной из критических точек, удовлетворяющих уравнениям
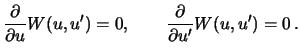
Функции
Используя алгебраическую технику базисов Гребнера [3], можно
исключить из уравнений (3) переменную ![]() . В результате
получаем тригонометрический многочлен
. В результате
получаем тригонометрический многочлен ![]() восьмой степени
восьмой степени
Соотношение ![]() необходимо и достаточно для совместности
системы (3). В невырожденном случае не существует многочлена
меньшей степени, обладающего этим свойством.
необходимо и достаточно для совместности
системы (3). В невырожденном случае не существует многочлена
меньшей степени, обладающего этим свойством.
Доказательство см в [1].
Опишем алгоритм определения ![]() .
На первом шаге решается уравнение
.
На первом шаге решается уравнение ![]() , т.е. находятся все его
вещественные корни на окружности
, т.е. находятся все его
вещественные корни на окружности ![]() . На втором шаге ищутся
соответствующие значения
. На втором шаге ищутся
соответствующие значения ![]() по формуле
по формуле
где
На третьем шаге сравнивается конечное множество значений ![]() и выбирается наименьшее
и выбирается наименьшее ![]() . В результате
. В результате
Рассмотрим вырожденные случаи, когда критические точки отвечают вещественным корням тригонометрического уравнения меньшей степени. Интуиция подсказывает, что простейшие вырождения связаны с двумя различными случаями: обращением в нуль взаимного наклона и хотя бы одного из эксцентриситетов. Как часто бывает, интуиция оправдывается лишь частично. Компланарность, в отличие от кругового случая, не ведет к вырождению.
1. Пусть орбита ![]() - круговая. Более того, допустимо считать
- круговая. Более того, допустимо считать
![]() , не пренебрегая первой степенью эксцентриситета. Полагая
, не пренебрегая первой степенью эксцентриситета. Полагая
![]() и используя процедуру факторизации, представим
и используя процедуру факторизации, представим ![]() в форме
в форме
2. Если исчезают оба эксцентриситета ![]() , то
, то ![]() и
и
Более того, ![]() содержит только вторые гармоники
содержит только вторые гармоники
3. Если в компланарном случае орбита ![]() - круговая, то
- круговая, то
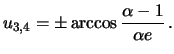
4. Наконец, обращение в нуль обоих эксцентриситетов и взаимного наклона влечет максимально вырожденный случай
<< 1. Введение | Оглавление | 3. Топология пар орбит >>
|
Публикации с ключевыми словами:
Небесная механика - кеплеровы орбиты
Публикации со словами: Небесная механика - кеплеровы орбиты | |
См. также:
Все публикации на ту же тему >> | |