§ 4.3 Белые карлики и нейтронные звезды
Рассмотрим теперь условия подобия звезд, построенных из вырожденного электронного газа. Как уже подчеркивалось, все политропные звезды с одинаковым индексом политропы подобны по своему строению. Уравнение состояния вырожденного электронного газа будет строгой политропой, если, во-первых, вторые члены в (4.9) или (4.10) малы, т. е. в пределе, когда по всему объему звезды вырожденный электронный газ является полностью нерелятивистским либо полностью релятивистским, и, во-вторых, температурными поправками можно пренебречь, т. е. малы и вторые члены в (4.5) и в (4.6) почти по всей массе белого карлика.
В пределе полностью нерелятивистского вырожденного электронного газа, т. е. при условии
|
|
(4.44) |
состояние газа описывается политропой с γ = 5/3 и мы получаем из (4.32) более точное выражение, чем (3.46):
|
|
(4.45) |
Из (4.44) и (4.45) следует, что нерелятивистскими белыми карликами являются звезды с относительно небольшой массой (как показывают оценки, M≲ 2μe-2M☉ ≈ 0,5M☉ ). По мере увеличения массы вырожденный электронный газ становится релятивистским сначала в центрах конфигураций, а затем, по мере перехода к большим массам, релятивизация охватывает и заметную часть массы звезды. Структура ее при этом меняется и постепенно переходит к структуре политропы с γ = 4/3. При таком переходе каждой массе соответствует своя конфигурация (они были рассчитаны Чандрасекаром [5]), но белые карлики с большей релятивизацией электронов опять становятся подобными в соответствии с политропой γ = 4/3.
Уравнение политропы релятивистского вырожденного электронного газа дано формулой (4.6). Поэтому условие (4.36), определяющее массу звезды с политропой γ = 4/3, приобретает вид
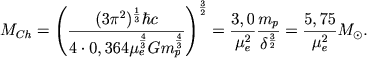
|
(4.46) |
Итак, все белые карлики, построенные из вырожденного релятивистского электронного газа, имеют почти одну и ту же массу, подобное строение и очень малый радиус. Согласно (4.10) и (4.37) радиус белого карлика уменьшается с ростом центральной плотности как R ∼ exp(-const ⋅ ρc2/3). Масса (4.46) есть предельная масса белого карлика, так называемый чандрасекаровский предел, который мы уже обсуждали в гл. 3. Следует отметить, что существование предела масс вырожденных звезд было показано советскими физиками Л. Д. Ландау и М. П. Бронштейном в более ранних работах, чем это было сделано Чандрасекаром.
Разумеется, структура белых карликов не определяется только простыми политропными соотношениями или даже более общим выражением для уравнения состояния вырожденного электронного газа (3.39) - (3.40). Например, структура белых карликов с большой плотностью должна рассчитываться с учетом эффектов общей теории относительности. Существенное влияние па их структуру оказывает быстрое вращение. Важное значение имеют и кристаллические свойства газа атомных ядер в недрах белых карликов, как это впервые было отмечено Д. А. Киржницем. Мы не будем обсуждать все эти свойства белых карликов, для пас важна была лишь та часть теории, которая рассматривает подобие белых карликов по крайней мере в первом приближении. Обзор исследований по различным эффектам, влияющим па структуру и свойства белых карликов, можно найти в книгах Шацмана [12], Г. С. Саакяна [13] и статье Местела в сборнике [9].
Энергетика белых карликов и их светимость тесно связаны с эволюцией этих звезд. К этому же кругу вопросов относятся и исследования недавно обнаруженных сильных магнитных полей у некоторых белых карликов. В.се эти проблемы, строго говоря, выходят за рамки настоящей книги, но некоторые расчеты изменения светимости со временем уже были рассмотрены в гл. 3.
Принцип подобия можно применить к исследованию строения белых карликов и при учете температурных эффектов, если считать, что в основной массе вырожденного газа температура Td, почти постоянна. Это более или менее справедливо в силу очень хорошей теплопроводности вырожденного электронного газа. Если подставить уравнения состояния (4.5) или (4.6) в первые два уравнения (4.31) при Т = Td = const, то получим при преобразовании (4.33) также первые два уравнения (4.34). Изменится только связь между безразмерными давлением и плотностью. Вместо определения давления как ![]() , теперь будем иметь соотношения
, теперь будем иметь соотношения
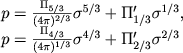
|
(4.47) |
для нерелятивистского и релятивистского белых карликов соответственно. Здесь П'1/3 и П'2/3 - новые безразмерные комплексы, определенные выражениями
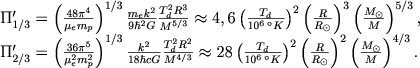
|
(4.48) |
Безразмерные комплексы П5/3 и П4/3 по-прежнему определяются формулой (4.32), где вместоK5/3 и K4/3 следует подставить соответствующие константы из уравнения состояния вырожденного электронного газа при T → 0.
Температурные добавки в (4.5) или (4.6) учитывают тепловое движение электронов. Но некоторый вклад в полное давление вносит и тепловое движение невырожденных ядер. Не будем выписывать полное выражение для всех поправок; приведем лишь формулу для случая, когда существенно только давление вырожденного электронного газа и газа атомных ядер. Этот случай встречается при относительно низких температурах, когда очень малы температурные добавки в (4.5) или (4.6), пропорциональные T2. Выражение для давления в безразмерных переменных имеет вид
|
|
(4.49) |
где П'1 - новый безразмерный комплекс, не зависящий от условия релятивизации электронов:
|
|
(4.50) |
Надо также иметь в виду, что, в отличие от (4.48), где величина μe есть молекулярный вес, приходящийся на один электрон (поэтому μe близко к двум), μe в (4.50) есть атомный молекулярный вес (для железного белого карлика μe ≈ 56).
Если температура внутри белого карлика порядка десятков миллионов .градусов, то безразмерные комплексы (4.48) и (4.50) много меньше единицы, поскольку радиусы белых карликов много меньше радиуса Солнца. Но па начальном этапе их эволюции эти параметры могут быть и большими.
Для определения структуры белых карликов с учетом температурных эффектов (в предположении изотермичности) следует решать систему (4.34) совместно с (4.47) или (4.49) при тех же граничных условиях (4.35). Правда, последние здесь становятся неточными, поскольку условие изотермичности заведомо несправедливо для наружных областей белых карликов. Их можно видоизменить так, чтобы учесть и падение температуры во внешних слоях.
Решение системы (4.34) теперь определяет связь между парами безразмерных комплексов: П5/3 и П'4/3; П4/3 и П'2/3; П5/3 и П'1; П4/3 и П'1. Это означает, что в этом случае мы находим связь между тремя параметрами - массой белого карлика, его радиусом и внутренней температурой как для случая нерелятивистского белого карлика, так и для релятивистского с массой вблизи верхнего предела, но еще имеющего конечный радиус.
Численное решение уравнений (4.34) с уравнениями состояния вырожденного газа, учитывающими температурные эффекты, было получено Г. М. Жислиным и В. И. Петрухиной. Предполагалась изотермичность вплоть до состояния, где температурные члены в три раза меньше давления вырожденного газа. В слоях, близких к поверхности, давление аппроксимировалось степенной формулой, учитывающей непрерывность давления и плотность. Результаты решения приведены в табл. 2.
Таблица 2
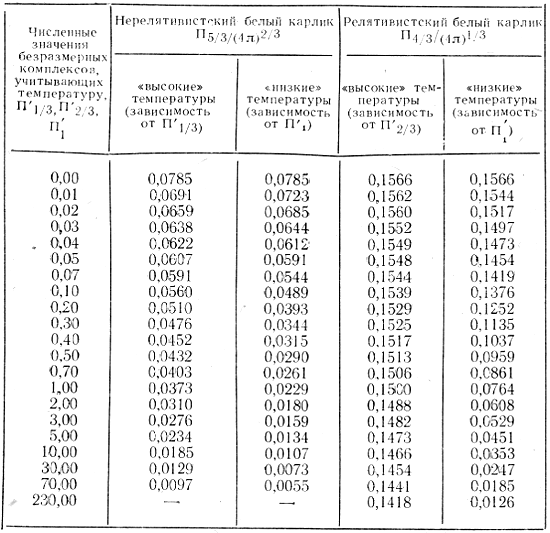
Здесь условно случаем "высоких температур" названо использование уравнения состояния (4.47), а случаем "низких температур" - уравнения состояния (4.49). Реальное значение имеют величины безразмерных комплексов П'1/3, П'2/3, П'1 меньше единицы, но расчеты проведены и для больших' значений этих комплексов для того, чтобы проследить соотношение между комплексами на большем интервале величин.
Пользоваться этой таблицей можно следующим образом. Рассмотрим для примера нерелятивистский белый карлик с уравнением состояния (4.47). Первый столбец таблицы дает функциональную зависимость ![]() которую можно переписать в виде
которую можно переписать в виде ![]() , где А и В - постоянные, выраженные через параметры уравнения состояния. Решая это уравнение (например, графически), можно найти, как меняется радиус белого карлика по мере изменения его внутренней температуры.
, где А и В - постоянные, выраженные через параметры уравнения состояния. Решая это уравнение (например, графически), можно найти, как меняется радиус белого карлика по мере изменения его внутренней температуры.
Рассматривая таблицу, можно убедиться, что пока П'1/3 и П'1 малы, изменения радиуса белых карликов с температурой невелики. Уравнения состояния (4.49) дает несколько больший эффект. Любопытно, что увеличение температуры уменьшает радиус белого карлика. Это связано с тем, что добавка тепловой энергии должна в рамках теоремы вириала увеличить абсолютное значение потенциальной энергии.
При значении безразмерных комплексов П'1/3 и П'1, сравнимых с единицей, изменения радиусов становятся более заметными, хотя, конечно, представление реального уравнения состояния в виде политропы с малыми температурными добавками становится все более грубым. Но для полукачественных оценок можно использовать и эти значения безразмерных комплексов.
В случае релятивистских белых карликов зависимость П4/3 и П'1 и особенно от П'2/3 выражена значительно слабее. Поскольку здесь П4/3 определяет только массу белого карлика ![]() , то увеличение Td эквивалентно увеличению предельной массы релятивистского белого карлика. Тепловая энергия требует увеличения абсолютного значения потенциальной энергии путем соответствующего изменения массы (также в соответствии с теоремой вириала). Хотя соответствующие изменения массы и невелики, но они могут сыграть существенную роль в эволюции звезд вблизи чандрасекаровского предела.
, то увеличение Td эквивалентно увеличению предельной массы релятивистского белого карлика. Тепловая энергия требует увеличения абсолютного значения потенциальной энергии путем соответствующего изменения массы (также в соответствии с теоремой вириала). Хотя соответствующие изменения массы и невелики, но они могут сыграть существенную роль в эволюции звезд вблизи чандрасекаровского предела.
Наконец сформулируем критерий подобия структуры белого карлика с учетом температурных эффектов. Будем называть структуры белых карликов подобными, если все определяющие комплексы одинаковы. У нерелятивистских белых карликов критерий подобия требует выполнения условий: ![]() ,
, ![]() , либо
, либо ![]() , откуда также следует
, откуда также следует ![]() как для уравнений состояния (4.47), так и для (4.49)). В случае релятивистских белых карликов условия подобия другие. Масса фиксирована значением П4/3, а из (4.48) и (4.50) следует, что подобны структуры белых карликов с температурными поправками, если
как для уравнений состояния (4.47), так и для (4.49)). В случае релятивистских белых карликов условия подобия другие. Масса фиксирована значением П4/3, а из (4.48) и (4.50) следует, что подобны структуры белых карликов с температурными поправками, если ![]() .
.
Наконец, рассмотрим случай конфигураций, состоящих из вырожденного нейтронного газа. В первом приближении нейтронные звезды подобны белым карликам, поскольку уравнения состояния различаются лишь разными значениями величины Kγ.
Если допустить, что звезда состоит только из нерелятивистского нейтронного газа и пренебречь силами ядерного взаимодействия между нейтронами, то все различие со случаем нерелятивистских белых карликов сводилось бы к замене me и mp на массу нейтрона mn и условию μe = 1. Например, согласно (3.45) радиус нейтронной звезды меньше радиуса белого карлика на множитель, равный отношению массы электрона к массе нейтрона, т. е.
|
|
(4.51) |
а предельная масса релятивистской нейтронной звезды равнялась бы 5,75 M☉.
Реальная картина, однако, сложнее. Во-первых, необходим учет взаимодействия между нейтронами. Во-вторых, всегда в нейтронном газе имеется примесь протонов и электронов, которых обычно не меньше 4-5%. В-третьих, близкие к поверхности слои нейтрон ной звезды состоят из обычного вещества, т. е. из электронов и атомных ядер. Частично это вещество находится в кристаллическом состоянии, а частично представляет собой плазму. Атомный вес ядер этого вещества меняется, увеличивается по мере погружения в глубь нейтронной звезды и лишь постепенно происходит переход к преимущественно нейтронному состоянию. В центральных частях более массивных нейтронных звезд имеются и гипероны.
Таким образом, политропная зависимость может рассматриваться только как первое, очень грубое приближение к реальному уравнению состояния нейтронного газа. Было проведено несколько расчетов уравнений состояния холодного (т. е. при T = 0) нейтронного газа. Одно из них, полученное Кануто [14], приведено на рис. 2. Касательная соответствует зависимости р ∼ ρ5/3. Можно отметить следующие особенности. Если исключить область относительно низких плотностей, где примесь нейтронов мала, в области умеренных и больших плотностей зависимость р ∼ ρ5/3 в первом приближении выполняется. Даже в области плотностей, больших ядерной, р ≳ 1015 г\см3, не видно перехода к релятивистской зависимости р ∼ ρ4/3. Здесь только уменьшается параметр K5/3. Величина этого параметра для нейтронных звезд с типичной средней плотностью порядка 1010-1014 г/см3
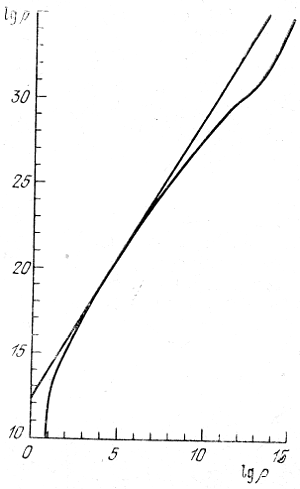
Рис. 2. Уравнение состояния нейтронного газа согласно Кануто. Касательная прямая соответствует зависимости р ∼ ρ5/3.
близка к ![]() . Подставляя это значение в соотношение (4.32), находим для радиуса нейтронных звезд:
. Подставляя это значение в соотношение (4.32), находим для радиуса нейтронных звезд:
|
|
(4.52) |
т. е. всего в два раза больше, чем в идеализированном случае (4.51). У нейтронных звезд с малой массой радиус может быть, вероятно, много больше. Здесь, с одной стороны, увеличивается множитель M-1/3, а с другой стороны, возрастает и параметр K5/3, поскольку меньше средние плотности. Кроме того, велик и вклад слоев, состоящих из обычного вещества. В последнее время было проведено несколько расчетов конкретных моделей нейтронных звезд. Мы не будем их обсуждать, поскольку нас в основном интересуют вопросы подобия моделей. Естественно, что уточненные расчеты дают сложную зависимость R(M), которая к тому же еще не получена с достаточной уверенностью.
Как отмечалось в гл. 3, верхний предел массы нейтронных звезд определялся из условия релятивистского вырождения нейтронного газа (предел Оппенгеймера - Волкова). Из рис. 2 следует, что этот предел соответствует переходу к очень большим плотностям, пока недоступным для более или менее строгого теоретического расчета уравнения состояния. Поэтому лучше оценить верхний предел массы нейтронной звезды так, как это сделано в формуле (3.53), потребовав, чтобы радиус нейтронной звезды не превышал гравитационного радиуса. Для модели идеального нейтронного газа, используя определение (4.51), находим
|
|
Учет реального уравнения состояния несколько увеличивает этот предел. Используя подобным образом формулу (4.52), получаем для. предела массы нейтронных звезд:
|
|
(4.53) |
Если потребовать, чтобы радиус нейтронной звезды был больше, например, 3Rg, тo предел массы будет ниже на множитель 33/4 ≈ 2,2.
При расчете очень плотных конфигураций уравнения гидростатического равновесия в ньютоновской форме становятся неприменимыми. В рамках общей теории относительности уравнение гидростатического равновесия имеет вид (3.53), потребовав, чтобы радиус нейтронной звезды не превышал гравитационного радиуса. Для модели идеального нейтронного газа, используя определение (4.51), находим
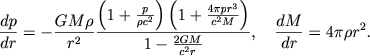
|
В таком виде к этому уравнению уже трудно (хотя и возможно) применять методы анализа размерностей и подобия. Здесь мы этого делать не будем, но отметим одно любопытное свойство этого уравнения (см. [15]). Если считать все вторые члены в скобках малыми по сравнению с единицей, то получим
|
|
Каждый из членов в круглой скобке заметно меняется на протяжении всего радиуса конфигурации, но их сумма меняется существенно медленнее. В центре конфигурации круглая скобка всегда равна 4рс/ρсс2, где рс и ρс - центральные давление и плотность. По мере перехода к поверхности величина круглой скобки меняется всегда на несколько десятков процентов даже в случае конфигурации с очень большой концентрацией к центру. Отсюда следует метод, предложенный в работе [15] для учета эффектов общей теории относительности: можно рассчитывать строение плотной звезды, пользуясь ньютоновскими уравнениями гидростатического равновесия, но заменяя постоянную Ньютона G на "эффективную величину гравитационного взаимодействия"
|
|
Для верхней точки графика рис. 2 получаем G' = 1,4G. Предел массы нейтронных звезд пропорционален G-3/2, поэтому учет эффектов общей теории относительности понижает этот предел как ![]() . Для максимальной плотности на графике рис. 2 получим уменьшение предельной массы до значения М ≤ 3,ЗМ☉, или еще меньше, если R > 3R☉. Возможно, что верхний предел масс нейтронных звезд не больше 2М☉.
. Для максимальной плотности на графике рис. 2 получим уменьшение предельной массы до значения М ≤ 3,ЗМ☉, или еще меньше, если R > 3R☉. Возможно, что верхний предел масс нейтронных звезд не больше 2М☉.
<< § 4.2 Политропные и конвективные звезды | Оглавление | § 4.4 Звезды с лучистым переносом энергии >>