Глава III. Основные характеристики звезд
Звезды - это, по-видимому, наиболее распространенные во Вселенной космические тела, имеющие вместе с тем относительно простую структуру. Со времени первых астрофизических наблюдений наши знания о звездах постоянно увеличиваются, причем открытия последних лет все время приносят неожиданности; достаточно вспомнить радиопульсары и рентгеновские источники в двойных системах. Однако все же принято считать, что главные законы, описывающие звездную физику, известны достаточно надежно, хотя неопределенный результат эксперимента с солнечными нейтрино вносит некоторые сомнения. В этой главе мы покажем, что основные соотношения, связывающие между собой параметры звезд, могут быть выведены с помощью простых соображений размерности. Более строгое рассмотрение звездных моделей с точки зрения их подобия будет дано в гл. 4
§ 3.1 Соотношение масса — светимость
В первую очередь займемся поиском зависимостей между характеристиками звезды. Основных параметров три: это масса М, радиус R и светимость L. В уравнение состояния вещества звезды входят универсальная газовая постоянная ℜ и безразмерный молекулярный вес μ. Как правило, структура звезды, в первую очередь ее термодинамические характеристики, определяется переносом энергии, генерируемой в ее центральных частях, через всю ее толщу. Наибольшую роль играет перенос энергии излучением, который можно характеризовать двумя определяющими параметрами - универсальной константой σ (постоянной закона Стефана-Больцмана) и коэффициентом поглощения ϰ , характеризующим "просачивание" излучения сквозь вещество. Будем относить ϰ к единице плотности.
Размерности определяющих параметров таковы:
![$$
\begin{array}{l} \quad [M] = \mbox{г}, \quad [R] = \mbox{см}, \quad [L] = \frac{\mbox{г} \cdot \mbox{см}^2}{\mbox{сек}^3}, \quad [G] = \frac{\mbox{см}^3}{\mbox{г} \cdot \mbox{см}^2}, \\ \\ \quad [\frac{\mathfrak {R}}{\mu}] = \frac{\mbox{см}^2}{\mbox{сек}^2 \cdot \mbox{град}}, \quad [\sigma] = \frac{\mbox{эрг}}{\mbox{сек} \cdot \mbox{см}^2 \cdot \mbox{град}^4} = \frac{\mbox{г}}{\mbox{сек}^3 \cdot \mbox{град}^4}, \\ \\ \quad [\varkappa] = \frac{1}{\mbox{см}} \cdot \frac{\mbox{см}^3}{\mbox{г}} = \frac{\mbox{см}^2}{\mbox{г}}.
\end{array}
$$](https://images.astronet.ru/pubd/2013/03/01/0001281314/tex/formula373.gif)
|
(3.1) |
Эту систему можно упростить. Размерность температуры (градус) входит только в два параметра - ℜ/μ и σ . Очевидно, что во все безразмерные комплексы может входить только такая комбинация этих двух параметров, в которой размерность градуса сокращается, а именно:
|
|
(3.2) |
Теперь остается шесть определяющих параметров с тремя независимыми размерностями. Составим матрицу размерности:
![$$
\begin{matrix}
\, & [M] & [L] & [R] & [G] & [\varkappa] & [\frac{\sigma \mu^4}{\mathfrak {R}^4}] \\
\mbox{г}&1&1&0&-1&-1&1 \\
\mbox{см}&0&2&1&3&2&8 \\
\mbox{сек}&0&-3&0&-2&0&5 \\
\end{matrix}
$$](https://images.astronet.ru/pubd/2013/03/01/0001281314/tex/formula375.gif)
|
(3.3) |
Ранг матрицы равен трем. Определяя безразмерный комплекс произведением
|
|
(3.4) |
получаем систему уравнений для показателей ki:
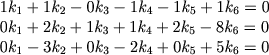
|
(3.5) |
имеющую три линейно независимых решения. Выберем их так, чтобы каждый безразмерный комплекс не включал бы в себя по очереди основные параметры R, L и ϰ . Кроме того, при этом будем учитывать некоторые физические соображения, которые станут ясными ниже.
Первый безразмерный комплекс выберем так, чтобы туда не входил радиус звезды (принимая k3 = 0). Для светимости примем показатель k2 = 1. Остается еще один произвольный параметр, который выберем так: k6 = - 1. Тогда имеем первый комплекс:
|
|
(3.6) |
Во втором безразмерном комплексе опустим светимость (k2 = 0), а заодно и член, описывающий поток излучения (k6 = 0). Положим также k1 = - 1. Тогда имеем
|
|
(3.7) |
где ![]() .
.
В третьем безразмерном комплексе опустим коэффициент непрозрачности (k5). Здесь можно также опустить термодинамические параметры (k6 = 0) и положить k2=1. Имеем
|
|
(3.8) |
Итак, мы получили три безразмерных комплекса, и искомое соотношение, теперь имеющее вид ƒ(П1, П2, П3) = 0, по-прежнему остается неопределенным до тех пор, пока мы не оценим порядки величин П1, П2, П3. Параметр П2 имеет очевидный смысл - это есть величина, обратная оптической толще звезды, отнесенной к ее средней плотности. Для всех реальных звезд величина этого комплекса на много порядков меньше единицы. Поэтому в дальнейшем всегда П2 можно пренебречь.
Физический смысл третьего безразмерного комплекса также несложен. Перепишем (3.8) в виде
![$$
\Pi_3 = L \left[\frac{GM^2}{R} \cdot \sqrt{\frac{GM}{R^3}}\right]^{-1}.
$$](https://images.astronet.ru/pubd/2013/03/01/0001281314/tex/formula382.gif)
|
(3.9) |
Согласно (2.28) GM2/R есть по порядку величины полная энергия звезды, а согласно (2.9) или (2.13) параметр (R3/GM)1/2 характеризует период колебания звезды или время ее сжатия в случае неустойчивости. Таким образом, безразмерный комплекс П3 был бы порядка единицы лишь в том случае, если бы звезда излучала свою полную энергию за время порядка периода колебаний или полного сжатия. Для некоторых быстрых этапов образования и эволюции звезд это условие действительно имеет место, но для стационарных звезд безразмерный комплекс П3 также на много порядков меньше единицы.
Остается комплекс П1 (3.6). Чтобы судить о нем, оценим прежде всего его величину для Солнца. Получим
|
|
(3.10) |
где, напоминаем, {ϰ} означает численное значение величины коэффициента непрозрачности.
Среднее значение коэффициента непрозрачности, рассчитанное для современных моделей Солнца, порядка или несколько больше единицы см2 ⋅ г-1, а величина молекулярного веса близка к 0,6, поэтому численное значение множителя П1 порядка 2-3. Итак, комплекс П1 действительно по порядку величины близок к единице.
Его физический смысл заключается в следующем. Стационарные звезды существуют только благодаря тому, что гравитационное притяжение компенсируется газовым давлением, для которого необходима высокая температура газа. В свою очередь температура вещества звезды определяется не только условиями генерации энергии, но и условием "просачивания" этой энергии через толщу звезды. Здесь должно иметь место некоторое самосогласование - в звезде данной массы должно генерироваться столько энергии, сколько ее может "просочиться" к поверхности. Отсюда и однозначная связь между светимостью, массой и коэффициентом непрозрачности. Эта связь, обнаруженная впервые и теоретически, и по данным наблюдений А. Эддингтоном еще в 1921 г., называется соотношением масса - светимость и является одной из важнейших астрофизических закономерностей. Приведенный выше элементарный вывод на основе соображений анализа размерностей позволяет соотношение масса - светимость записать в виде
|
|
(3.11) |
Формула (3.11) удовлетворительно описывает светимость Солнца и дает, по крайней мере качественное, согласие с наблюдаемой зависимостью масса - светимость. Количественные расхождения с наблюдаемой зависимостью, однако, достаточно заметны. Причин для этого несколько. При выводе этой формулы предполагается, что коэффициент непрозрачности постоянен по всей звезде и одинаков у звезд разных масс. На самом деле это выполняется только в том случае, если непрозрачность объясняется томсоновским рассеянием. Тогда, действительно, L ∼ M3. Другие механизмы поглощения света приводят к существенной зависимости ϰ от плотности и особенно от температуры. Это приводит к более сложной зависимости светимости от массы, которая будет получена в следующей главе.
Кроме того, соотношение масса - светимость зависит, хотя и слабее, от закона выделения энергии. Тем не менее формула (3.11) сохраняет свое методическое значение прежде всего в силу своей элементарности. Ее обсуждение позволяет просто объяснить многие явления физики звезд (см. изложение в [1]).
<< § 2.3 Характерные параметры твердых планет | Оглавление | § 3.2 Равсновесие и устойчивость звезд >>