§ 3.3 Белые карлики, нейтронные звезды и "черные дыры"
Другим примером звезд с однозначной зависимостью давления от плотности являются звезды, состоящие из вырожденного газа. Эти звезды также удобно изучать методом теории размерностей.
Напомним физику этого явления. Рассмотрим газ из свободных электронов. (В силу принципа Паули в одном квантовомеханическом состоянии (без учета спина), т.е. в одной квантовой ячейке фазового пространства, может находиться не более двух электронов. При большой пространственной плотности электронов на один электрон приходится малый геометрический объем и, следовательно, большой объем пространства импульсов. Иными словами, при большой плотности импульсы свободных электронов должны быть велики, даже если их температура равна нулю. Газ свободных электронов при больших их концентрациях ne, имеет высокое давление и при Т = 0. Ясно, что это давление вырожденного электронного газа может противостоять силе тяготения и тем самым обеспечить существование особого типа звезд. Такие звезды действительно были открыты более 50 лет назад и их называют белыми карликами (или "черными" карликами, если у них Т → 0).
Уравнения состояния вырожденного электронного газа выводятся в рамках квантовой статистической физики и его можно найти во многих учебниках. Но оказывается, что эти же уравнения могут быть получены элементарнейшим образом методом теории анализа размерностей без использования сложного аппарата квантовой механики.
Запишем определяющие параметры задачи. Два из них очевидны - давление p и электронная концентрация ne. Поскольку само явление вырождения электронного газа связано с квантовыми свойствами, то в число определяющих параметров должна входить постоянная Планка ħ. При больших плотностях электроны могут стать релятивистскими - учтем в определяющих параметрах и скорость света c. Сам электрон характеризуется массой me и зарядом e, но если кулоновским отталкиванием между электронами можно пренебречь, то останется лишь параметр me. Температуру газа будем считать равной нулю, а следовательно, и давлением ионной компоненты также можно пренебречь.
Составим матрицу размерности для приведенных выше параметров:
![$$
\begin{matrix}
\, & [p] & [n_e] & [\hbar] & [c] & [m_e] \\
\mbox{г}&1&0&1&1&1 \\
\mbox{см}&-1&-3&2&1&0 \\
\mbox{сек}&-2&0&-1&-1&0\\
\end{matrix}
$$](https://images.astronet.ru/pubd/2013/03/01/0001281314/tex/formula346.gif)
|
Ранг матрицы равен трем и, следовательно, здесь есть два независимых безразмерных комплекса. Выберем их так, чтобы в один из них была бы включена масса me, но опущена скорость света c, а в другом, наоборот, сохранена c, но опущена me. Получим
|
|
(3.36) |
|
|
(3.37) |
Поскольку имеются два безразмерных комплекса, то полное уравнение состояния вырожденного электронного газа при нулевой температуре можно записать как
|
|
(3.38) |
где функция ƒ(П1, П2) из соображений анализа размерностей не определяется. Точное вычисление на основе квантовой механики с учетом эффектов теории относительности дает следующее сложное выражение:
|
|
(3.39) |
где через х и у обозначены следующие комбинации:
|
|
(3.40) |
Уравнение состояния (3.39) - (3.40) - полное, учитывающее как релятивистские, так и нерелятивистские электроны. В предельных случаях относительно небольшой или очень большой электронной концентрации можно получить уравнение состояния и не прибегая к определению функции (3.38).
В случае относительно малой концентрации электронов даже наиболее быстрые из них имеют скорости, существенно меньшие, чем скорость света. Иными словами, в этом случае с не является определяющим параметром или, что одно и то же, можно считать П2 << 1.
Из соображений анализа размерностей следует, что в случае нерелятивистского вырожденного электронного газа уравнение состояния определяется формулой (3.36) при П1=const. Квантовая механика дает значение П1 которое можно также получить из (3.39) и (3.40), если перейти к пределу П2 → 0. В результате получаем
|
|
(3.41) |
т.е. П1 = 1,95.
В случае очень большой электронной плотности скорости большей части электронов близки к скорости света и П2 не малó . Но зато в этом случае можно пренебречь комплексом П1. В самом деле, масса покоя релятивистских частиц существенного значения не имеет и, по существу, me не есть определяющий параметр. Считан П1 << 1, из соображений теории анализа размерностей получаем уравнение состояния (3.37) при П2 = const. С учетом численного множителя, который можно получить и из (3.39) при разложении по П1 << 1, имеем уравнение состояния релятивистского вырожденного электронного газа:
|
|
(3.42) |
В этом случае безразмерный комплекс П2 = 0,78 - т. е. тоже очень близок к единице. Поэтому, даже совсем не используя квантовую механику (т. е. не зная численных значений П1 и П2), можно получить уравнение состояния с большой точностью только из одних соображений теории анализа размерностей.
Если включить в число определяющих параметров и температуру, то можно получить критерии вырождения. Более полные уравнения с учетом температурных эффектов состояния будут приведены в следующей главе.
Вещество в целом должно быть электрически нейтрально. Поэтому концентрация электронов определяет и концентрацию тяжелых частиц. Обозначим через ре молекулярный вес тяжелых частиц, приходящихся на один электрон. У белых карликов различного химического состава величина μe обычно лишь немного превышает двойку. Отсюда для плотности вещества белых карликов имеем
|
|
(3.43) |
где mp - масса протона. Теперь оба уравнения состояния примут вид
|
|
(3.44) |
для нерелятивистского газа, и
|
|
(3.45) |
для релятивистского электронного газа. (В обоих предельных случаях мы получим политропные соотношения с показателями γ = 5/3 и γ = 4/3 соответственно.
Приведенный здесь вывод уравнений состояния вырожденного электронного газа наглядно иллюстрирует возможности метода анализа размерностей. Используя соотношения (3.44) и (3.45), можно теперь оценить параметры белых карликов. В случае звезд малой массы, когда даже в центре белых карликов нет релятивистских электронов, можно использовать для давления формулу (3.44). Так как здесь γ = 5/3, то из (3.17) следует для радиуса звезды:
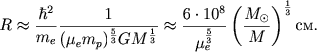
|
(3.46) |
Здесь опущены численные множители, которые более точно будут определены в следующей главе.
Формула (3.46) справедлива лишь для звезд малых масс (М < 0,5 М☉). С увеличением массы увеличивается и центральная плотность белых карликов (уменьшается радиус). Из-за этого в их центрах увеличивается степень релятивизации и надо постепенно переходить к уравнению состояния (3.45), точнее, надо строить модели с полным уравнением состояния (3.39) - (3.40).
Однако в пределе наибольших плотностей почти для всей массы белого карлика справедливо уравнение состояния (3.45) и такой белый карлик описывается политропой с γ = 4/3. Из (3.19) следует, что у подобной звезды фиксирована лишь масса. Согласно (3.19), опуская множители порядка единицы, имеем
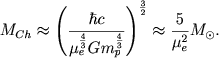
|
(3.47) |
Величина (3.47) (ее точное выражение будет приведено в гл. 4) называется чандрасекаровским пределом. Масса белых карликов не может быть больше этой величины.
Радиус политропы с γ = 4/3 не определен. Но поскольку электронный газ в белых карликах даже с очень большой центральной плотностью все же остается нерелятивистским в его поверхностных слоях, то здесь нет "чистой" политропы γ = 4/3. Среднее "эффективное" γ немного больше и поэтому сохраняется зависимость - уменьшение (радиуса с увеличением массы. Это означает, что по мере приближения массы белого карлика к чандраоекаровскому пределу его радиус уменьшается и стремится к нулю по мере достижения этого предела. Расчеты с уравнением состояния (3.39) - (3.40) подтверждают этот вывод (см. подробнее [3]).
Важной особенностью звезд типа белых карликов является однозначная зависимость между его радиусом, массой и электронным молекулярным весом, которая легко видна уже из (3.46). Электронный молекулярный вес меняется в небольших пределах, и у всех белых карликов должен быть близок к двум. Поэтому в первом приближении радиус белого карлика более или менее однозначно определяется его массой. Этот теоретический вывод в принципе можно использовать для определения масс белых карликов. Например, гравитационное красное смещение в спектрах белых карликов,
|
|
(3.48) |
Не совсем ясен вклад атмосферы белого карлика, нет уверенного метода выделения гравитационной части из общего смещения спектральных линий и т. п. По-прежнему массы белых карликов определяются почти исключительно по их орбитальному движению в двойных системах, а измерение гравитационного красного смещения используется лишь для сопоставления с теоретической зависимостью между М и R. Наблюдательный материал очень небогат, но качественное согласие теории и наблюдений имеется.
Более подробно теорию белых карликов мы будем обсуждать в следующей главе. При очень больших плотностях становится неустойчивым состояние газа, в котором имеются атомные ядра и вырожденные электроны. Здесь электроны как бы "вдавливаются" в ядра, превращая протоны в нейтроны. Ядра распадаются, в веществе появляется примесь свободных нейтронов, а при еще больших плотностях вещество превращается в нейтронный газ.
Нейтронный газ также оказывается вырожденным. Состоящие из такого вещества звезды и есть нейтронные звезды, ставшие в последнее время очень популярными в связи с открытием пульсаров и рентгеновских источников. Расчеты моделей нейтронных звезд проводились неоднократно. Трудности здесь в том, что неизвестно более или менее точное уравнение состояния нейтронного газа.
Но для простых оценок мы можем использовать уже известные соотношения. Формулы, полученные выше из соображений анализа размерностей, справедливы, разумеется, и в том случае, если мы вместо электронов будем понимать нейтроны. Вся разница в том, что me и mp следует заменить на mn - массу нейтрона, а μe считать равной единице.
Уравнение состояния нерелятивистского вырожденного нейтронного газа есть
|
|
(3.49) |
где nn - концентрация нейтронов. Численного множителя здесь нет из-за отсутствия точной теории.
Для релятивистского вырожденного нейтронного газа
|
|
(3.50) |
У нейтронной звезды, состоящей из нерелятивистского вырожденного нейтронного газа, также есть однозначная зависимость между массой и радиусом, аналогичная (3.46):
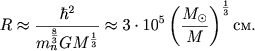
|
(3.51) |
С точностью до численных множителей, которые можно получить только из точной теории, радиус нейтронной звезды меньше радиуса белого карлика на множитель, равный отношению массы электрона к массе нейтрона.
С увеличением массы звезды плотность нейтронного газа увеличивается и он становится релятивистским. Происходит приближение к политропе γ = 4/3, в результате чего и нейтронные звезды имеют предел массы (предел Оппенгеймера - Волкова), по порядку величины близкий к (3.47):
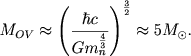
|
(3.52) |
На самом деле численное значение недостаточно точно, поскольку здесь есть еще множители порядка единицы, точное значение которых пока не известно. Различные модели дают для верхнего предела массы нейтронных звезд величину около 2-3 масс Солнца.
Можно получить еще один способ оценки верхнего предела массы стационарных нейтронных звезд. Радиус любого стационарного тела должен быть больше его гравитационного радиуса Rg=2GM/c2. Учитывая (3.51), имеем
|
|
(3.53) |
Отсюда, с точностью до множителя 2-4/3, также следует предел (3.52).
Радиус нейтронных звезд обычно всего в несколько раз превышает их гравитационный радиус, поэтому эффект общей теории относительности весьма существен. Еще важнее он для звезд с массой, большей предела (3.52). В этом случае никакое давление вещества не в состоянии противостоять силе гравитационного притяжения и подобные звезды должны сжиматься, уходя под свою "поверхность Шварцшильда" - сферу с радиусом, равным гравитационному радиусу. Образуются так называемые "черные дыры" или "застывшие звезды". Собственное излучение с поверхности этих звезд не выходит, но они благодаря своему мощному гравитационному полю притягивают вещество (аккреция), которое при падении на подобное тело разогревается и излучает в рентгеновском диапазоне (см. гл. 2).
Мощность излучения можно определить по скорости аккреции, для которой соответствующие формулы были получены из соображений анализа размерностей (см. (2.30) - (2.31)). Наибольший разогрев и, следовательно, наибольшая мощность излучения аккрецирующего газа идет из области, окружающей "черную дыру" примерно на расстоянии трех гравитационных радиусов. Надо также иметь в виду, что часто эта аккреция имеет несимметричный характер. В тех случаях, когда "черная дыра" входит в состав тесной двойной системы (здесь обычно аккреция наибольшая), газ, притягиваемый к "черной дыре", образует сначала диск и только потом выпадает на "дыру". Влияет на аккрецию и магнитное поле. Для грубой оценки можно считать, что "площадь аккреции" порядка ![]() . Поскольку на расстоянии 3Rg скорость движения около
. Поскольку на расстоянии 3Rg скорость движения около ![]() скорости света, то энергия, выделяемая при аккреции газа за единицу времени,
скорости света, то энергия, выделяемая при аккреции газа за единицу времени,
|
|
(3.54) |
где ρ - плотность аккрецирующего вещества вблизи тела; принято также ![]() . Но светимость любого объекта не может быть больше эддингтоновского предела (3.34) - (3.45), который можно записать в виде
. Но светимость любого объекта не может быть больше эддингтоновского предела (3.34) - (3.45), который можно записать в виде
|
|
(3.55) |
где, напоминаем, r0 есть классический радиус электрона. Отсюда стационарная аккреция возможна лишь при
|
|
(3.56) |
Легко убедиться, что мощное излучение при аккреции на "черные дыры" сосредоточено в рентгеновском диапазоне. В самом деле, поток излучения с единицы поверхности равен
|
|
(3.57) |
Здесь предполагается, что излучение идет с поверхности, радиус которой в три раза больше гравитационного радиуса. Яркостная температура этого излучения
![$$
T \approx \sqrt[4]{\frac{L}{4\pi R^2 \sigma}} \approx \frac{1}{3}\sqrt[4]{\frac{m_p c^3}{r_0^2 R_g}} \approx 10^7 \mbox{град},
$$](https://images.astronet.ru/pubd/2013/03/01/0001281314/tex/formula372.gif)
|
(3.58) |
что и соответствует рентгеновскому диапазону (длина волны λ ≈ 1 - 10 Å). Рентгеновские источники в тесных двойных системах, где можно ожидать существенной аккреции за счет перетекания вещества от одной звезды к другой, и есть наиболее вероятное проявление существования "черных дыр" (объект Лебедь Х-1). Масса этого объекта порядка 10-12 масс Солнца, т. е. много больше массы стационарных звезд, состоящих из вырожденного газа.
<< § 3.2 Равсновесие и устойчивость звезд | Оглавление | § 3.4 Характерные времена отдельных этапов эволюции звезд >>