§ 4.2 Политропные и конвективные звезды
Рассмотрим сначала более простой случай, когда давление вещества и его плотность повсюду внутри звезды связаны простой однозначной политропной зависимостью. Как уже отмечалось, приближенно такими свойствами обладают либо те звезды, в которых энергия целиком переносится конвекцией, либо звезды, давление в которых связано в основном с вырождением электронного или нейтронного газа.
Правда, в реальных звездах политропная зависимость с одними и теми же значениями Kγ и γ не может описывать всей структуры. Наружные слои белых карликов состоят из невырожденного газа, в их центральных частях электроны частично становятся релятивистскими. Показатель γ у конвективных звезд меняется с глубиной, да и мало вероятно существование звезд, у которых по всей толще энергия переносится конвекцией - по крайней мере в ее атмосферных слоях появляется и лучистый перенос. Тем не менее рассмотрение политропных моделей с постоянными Kγ и γ оказывается очень полезным. Их можно считать первым приближением к звездным моделям и изучать на основе политропных моделей некоторые свойства звезд. Наконец, здесь нагляднее всего иллюстрируется принцип подобия звездных моделей. В этом параграфе будут рассмотрены общие политропные модели. Затем мы обсудим очень простой случай полностью конвективных звезд. Белые карлики и звезды будут рассмотрены в следующем параграфе.
Запишем снова основные уравнения политропной модели:
|
|
(4.31) |
Этих уравнений достаточно для решения задачи.
Сформулируем теперь граничные условия. В центре звезды при r → 0 первого уравнения имеется особая точка; очевидно, что здесь должно быть М(r) → 0. Кроме того, из физических соображений можно потребовать ограниченности плотности и давления в центре звезды. Наружную границу звезды определим условием ρ = 0. Очевидно, что в этом случае согласно (4.31) и давление должно стремиться к нулю.
Прежде чем заниматься решением уравнений (4.31), воспользуемся соображениями анализа размерностей, учитывая основные параметры звезды. Очевидно, что таковыми являются только полная масса М и радиус R объекта. Определяющим параметром также является и "политропная температура" Kγ. Из четырех определяющих параметров: М, R, G и Kγ составляется одна безразмерная комбинация, которую мы уже определили в гл. 3 формулой (3.17):
|
|
(4.32) |
Численное значение Πγ из соображений анализа размерностей не определяется, поэтому в гл. 3 эта величина осталась произвольной. Теперь мы ее найдем из уравнений (4.31). Приведем их к безразмерному виду введением новых безразмерных переменных:
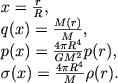
|
(4.33) |
Тогда получим
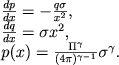
|
(4.34) |
где Πγ - тот же безразмерный комплекс (4.32).
Система (4.34) должна решаться при следующих граничных условиях, записанных в безразмерных переменных:
|
|
(4.35) |
Очевидно, что уравнения (4.34) и условия (4.35) являются типичной задачей на собственные значения. Решение этих уравнений, удовлетворяющих граничным условиям (4.35), возможно только при определенном значении единственного численного параметра Πγ. Численное решение системы (4.34) - (4.35) и позволяет определять параметры Πγ. Эти данные приведены в табл. 1 (численные значения комплексов для других значений γ можно найти в [5]):
| γ | 3 | 2 | 5/3 | 3/2 | 4/3 | 5/4 |
| 2,270 | 0,637 | 0,424 | 0,365 | 0,364 | 0,477 | |
| 1,836 | 3,290 | 5,991 | 11,043 | 54,183 | 622,408 |
В последней строке таблицы приведено отношение центральной плотности конфигурации к ее средней плотности - величина, в три раза меньшая значения безразмерной функции σ(0) в центре конфигурации.
То, что мы сделали выше, и есть применение принципа подобия. Звезды с одинаковым индексом политропы у имеют одинаковое строение, одинаковую концентрацию вещества к центру. Радиусы звезд разных масс, но построенных по одинаковой политропе, определяются по соотношению (4.32). Важно, что применение принципа подобия позволило определить и численное значение параметра Πγ - в этом и проявляется преимущество метода подобия перед простым анализом размерностей, применимом в случае, когда имеются точные уравнения, описывающие само явление.
Свойства политропных моделей неоднократно исследовались самым общим образом (см., например, работу [5]). Здесь они также рассматривались в гл. 3, где к полученным там результатам можно теперь добавить значение численного безразмерного комплекса Πγ. В частности, имеем следующее точное выражение для массы звезды с политропным показателем γ = 4/3 и данной политропной температурой
|
|
(4.36) |
Из численных значений величии Πγ, приведенных выше, следует, что в области γ ≈ 1,5 - 1,33 величина Πγ почти не меняется при изменении γ. Это обстоятельство позволяет сделать другой важный вывод. Рассмотрим последовательность политропных моделей, имеющих одинаковую массу M0, одинаковое значение Kγ, но различные значения γ в небольшом интервале 1,35 < γ < 1,5. Здесь почти одинаковы и Πγ. Такую последовательность всегда можно осуществить, поскольку при γ ≠ 4/3 масса политропной модели может быть произвольной. Посмотрим теперь, как меняется радиус у этой последовательности моделей при уменьшении γ . Из (4.36) следует:
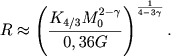
|
(4.37) |
Будем теперь приближать γ к 4/3. Показатель 1/(4-2γ) стремится к -∞, а величина в скобках остается большей единицы, если M0 > M4/3. Отсюда следует, что радиусы таких моделей стремятся к нулю. Это и есть доказательство коллапса звездных моделей с массой, большей предела (4.36), при стремлении показателя γ к 4/3 сверху.
Перейдем теперь к рассмотрению моделей полностью конвективных звезд. Как правило, конвективный перенос энергии имеет место в относительно холодных звездах, где β ≈ 1 и где поэтому γ = 5/3. Это условие будем считать выполненным. Величина K5/3 в политропной отношении р=K5/3ρ5/3 зависит от энтропии газа, которая считается постоянной по всей массе звезды. Напомним, что мы предполагаем конвекцию адиабатической. Но лучше параметр K5/3 выразить через центральную температуру звезды Tc. Учтем также, что центральная плотность политропы с γ = 5/3 больше средней в 5,991 раз. Имеем
|
|
(4.38) |
Возвращаясь к основному соотношению (4.32), получаем связь между тремя основными параметрами М, R и Т:
|
|
(4.39) |
Если считать массу звезды заданной, то одного соотношения (4.39) недостаточно для определения радиуса или центральной температуры звезды. Необходимы дополнительные связи, которые должны включать и новые параметры, характеризующие звезду.
Очевидно, что таким параметром должна быть светимость, также характеризующая центральную температуру звезды. Предположим, что источники энергии описываются общим соотношением (4.24). Распределение плотности и температуры в звезде задано условием конвективного переноса энергии и поэтому достаточно вычислить просто первый интеграл (4.15) при r ≈ R. Переходя к безразмерным переменным (4.33) и учитывая, что
|
|
находим
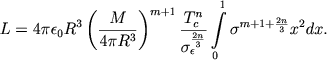
|
(4.40) |
Степень m + 1 + 2n/З достаточно велика у всех типов термоядерных реакций. Поэтому выделение энергии сосредоточено только в небольшом объеме вблизи центра звезды. Это означает, что можно вычислить интеграл в (4.40), воспользовавшись подходящей аппроксимацией σ(х) при x → 0. Удобным соотношением, справедливым для политропы с любым показателем, является формула
|
|
(4.41) |
которая удовлетворяет также необходимому условию dσ/dx = 0 при x=0. Подставляя (4.41) в (4.40), находим окончательно:
|
|
(4.42) |
Это и есть искомое выражение светимости через М, R и Tc. Исключая из (4.42) и (4.39) центральную температуру Tc, получим одно соотношение между М, L и R. Эта формула имеет вид
|
|
(4.43) |
У холодных звезд с конвективным переносом основным источником энергии является протонная реакция при n ≈ 6 и m = 1. Тогда из (4.43) имеем
|
|
Второе соотношение, связывающее эти три параметра, может быть получено из анализа условий в звездных атмосферах. Приближенно это сделать трудно, даже выполнение численных расчетов на ЭВМ связано с преодолением многих сложных проблем. Поэтому мы здесь не будем этим заниматься. Кроме того, предположение о полностью конвективной модели является далеко идущей идеализацией. Теоретические расчеты дают для холодных звезд-карликов зависимость L ∼ М1,7, но у них имеются и области с лучистым переносом энергии.
Несколько более подробно модели звезд, в том числе и тех из них, где существенна роль конвективного переноса энергии, обсуждаются в последнем параграфе этой главы.
<< § 4.1 Основные уравнения теории внутреннего строения звезд | Оглавление | § 4.3 Белые карлики и нейтронные звезды >>