4.4 Некоторые применения
Несомненно, что выведенные нами формулы должны приниматься во внимание при решении многих вопросов, касающихся туманных оболочек, окружающих звезды. Некоторые из этих вопросов рассмотрены ниже.
а) Неоднородная оболочка
В главе II к неоднородным оболочкам звезд мы применили результаты, полученные нами в главе I для однородной среды. Тогда мы не могли обосновать законность этого применения, так как в нашем распоряжении не было уравнения переноса излучения в спектральной линии. Мы сделаем это сейчас, взяв для простоты атом с тремя уровнями.
В данном случае плотность излучения в линии определяется вторым из уравнений (22), в котором все величины β, γ и ![]() являются заданными функциями от r. Наше приближение состоит в том, что в средних частях оболочки плотность излучения в линии считается равной
являются заданными функциями от r. Наше приближение состоит в том, что в средних частях оболочки плотность излучения в линии считается равной
|
|
(65) |
Из указанного уравнения вытекает следующее неравенство, дающее оценку условий, при которых это приближение является справедливым:
|
|
(66) |
Для модели оболочки, рассмотренной в главе II, мы имеем
![]()
что β >> γ так как в обратном случае распределение атомов по состояниям во всей оболочке является близким к больцмановскому. Для такой оболочки неравенство (66) приводится к виду
|
|
(67) |
Так как обычно ![]() , то это неравенство на всем протяжении оболочки может считаться выполненным в весьма сильной степени.
, то это неравенство на всем протяжении оболочки может считаться выполненным в весьма сильной степени.
б) Температура звезд
Как известно, метод Zanstra для определения температур звезд, окруженных небулярными оболочками, основан на предположении, что свечение оболочки в линиях какого-либо элемента происходит за счет энергии звезды за границей основной серии. Однако в случае оболочек малого радиуса в излучение линий переходит не только энергия звезды за границей основной серии, но и за границами субординатных серий. Поэтому температуры звезд, определяемые методом Zanstra без учета этого обстоятельства, могут оказаться завышенными.
Горделадзе [4] оценил величину этого эффекта, используя теорию возбуждения и ионизации в оболочках малого радиуса, данную В. А. Амбарцумяном [1]. Он нашел, что в случае звезд типа Вольфа-Райе температуры, определенные по линиям ионизованного гелия и других атомов с высоким потенциалом ионизации, получающиеся гораздо более высокими, чем по линиям водорода, должны быть при учете этого эффекта значительно понижены.
Однако теория В. А. Амбарцумяна не учитывает движения оболочки. Мы сейчас оценим величину этого эффект, используя наши формулы, полученные выше. Пусть оболочка поглощает всю энергию звезды за границей основной серии. Число поглощенных квантов будет равно
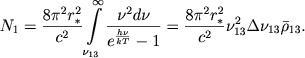
|
(68) |
Найдем теперь число квантов за границей субординатной серии, поглощенных оболочкой. Мы, очевидно, имеем
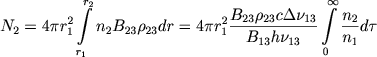
|
(69) |
|
|
(70) |
|
|
(71) |
Это выражение должно быть подставлено в следующее уравнение
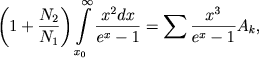
|
(72) |
являющееся обобщением уравнения Zanstra (III,60). Здесь суммирование ведется по линиям рассматриваемого атома.
Вычисления показывают, что величина γ/β обычно порядка единицы. Поэтому мы приходим к выводу, что рассматриваемый эффект не играет заметной роли (для ионизованного гелия эта величина должна быть порядка 108, чтобы температура звезды "повысилась" с 20000°; до 50000°;). Действительное объяснение указанного выше расхождения между температурами, определенными по линиям различных атомов, дано в § 1 главы II.
в) Температура оболочек
опрос о температурах оболочек малого радиуса (в частности - оболочек новых звезд) является в настоящее время Совершенно неясным. Обычно считается, что температура оболочки просто равна температуре звезды. Для выяснения этого вопроса, принципиально говоря, можно использовать метод, предложенный нами для определения температур газовых туманностей (глава III, § 3). Однако из-за сложности явлений, происходящих в оболочках малого радиуса, точные подсчеты пока затруднительны.
Мы все же можем отметить одно обстоятельство, отличающее оболочки малого радиуса от газовых туманностей. Так как ионизация в этих оболочках происходит не только из основного, но и из возбужденных состояний, то средняя энергия, получаемая электронами при ионизации, в этом случае значительно меньше, чем в туманностях. Проведем иллюстративный подсчет для водородной оболочки, пренебрегая столкновениями.
Условие равенства числа ионизации и рекомбинаций к закон сохранения энергии для свободных электронов оболочки могут быть записаны в виде
|
|
(73) |
|
|
(74) |
где εic есть средняя энергия, получаемая электроном при фотоионизации с i-гo уровня, а остальные обозначения приняты такими же, как в § 3 главы III.
Допустим, как и раньше, что оптическая толщина оболочки за границей основной серии гораздо больше единицы а за границами субординатных серий меньше единицы. Тогда все кванты, излучаемые оболочкой за границей основной серии, будут поглощаться в самой оболочке. Поэтому вместо (73) и (74) мы получаем
|
|
(75) |
|
|
(76) |
где через ρic0 обозначена плотность излучения, приходящего непосредственно от звезды, а через εic0 - соответствующая энергия, получаемая электроном при ионизации.
Пусть Ni есть число ионизаций, происходящих из i-го состояния во всей оболочке, т. е.
|
|
(77) |
Из соотношений (75) и (76) мы находим
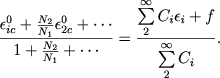
|
(78) |
Так же, как в главе III, это соотношение может быть преобразовано к виду
|
|
(79) |
где величина A1 определяется формулой (III, 42), а величины A2, A3, ... - формулой (41), в которой надо считать ![]() (ибо за границей основной серии поглощается все излучение, идущее от звезды, а за границами субординатных серий - только небольшая часть излучения). Соотношение (79) дает искомую связь между T∗ и Te.
(ибо за границей основной серии поглощается все излучение, идущее от звезды, а за границами субординатных серий - только небольшая часть излучения). Соотношение (79) дает искомую связь между T∗ и Te.
Допустим для примера, что больше всего ионизаций происходит из второго состояния. Тогда вместо (79) имеем
|
|
(80) |
При T∗=20000°; из табл. XI находим A2=0,71 (это значение берется из первой части указанной таблицы при температуре в 4 раза большей температуры звезды). С этим значением A2 для электронной температуры получаем Te=12000°;. Заметим, что если бы было N2/N1 < 1, то для Te получилось бы значение порядка 20000°; .
Как уже сказано, проведенный подсчет не претендует на точность, ибо мы не учитывали столкновений, которые могут как понижать, так и повышать температуру оболочки (соответственно удары первого и второго рода).
Следует также иметь в виду, что температура разных частей оболочки может быть различной. В таком случае температура внешних частей должна быть более низкой, чем внутренних. Это обусловлено двумя причинами: 1) падением степени возбуждения и ионизации при переходе от внутренней границы оболочки к внешней и 2) полным экранированием излучения звезды за границей основной серии. Вследствие этого электроны получают при ионизации небольшую энергию и не могут ее увеличить за счет ударов второго рода.
г) Световое давление
Несомненно, что световое давление, вызванное поглощением света в спектральных линиях, играет в оболочках новых звезд значительную роль. Для применений важно дать формулы, определяющие следующие величины: 1) световое давление на внутренней границе оболочки и 2) световое давление, действующее на всю оболочку.
Чтобы получить эти формулы, мы можем воспользоваться результатами, найденными в § 1 настоящей главы. Определяя произвольные постоянные, входящие в выражения (23) и (24), из граничных условий (30), мы для потока излучения на внутренней границе оболочки находим
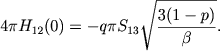
|
(81) |
Световое давление, вычисленное с помощью этой формулы, оказывается по порядку величины сравнимым с силой притяжения центральной звезды.
При получении формулы (81) мы пренебрегли излучением в линии, падающим на внутреннюю границу оболочки от звезды. Если учесть это излучение, то к потоку излучения (81) придется прибавить следующий член:
|
|
(82) |
Надо думать, что этот член гораздо меньше предыдущего, так как отношение S13/S12 , т. е. отношение числа квантов за границей основной серии к числу квантов в линии, разумеется, очень велико.
Заметим, что для объяснения явлений, происходящих в оболочках новых звезд сразу после максимума блеска, Э. Р. Мустель [5,6] предполагает, что основной силой, действующей в оболочке в этот период, является световое давление, вызванное поглощением квантов, идущих непосредственно от звезды. Поток излучения на внутренней границе оболочки при этом равен
|
|
(83) |
Чтобы согласовать это предположение с нашими результатами, надо потребовать выполнения одного из двух условий: 1) градиент скорости в оболочке очень велик, а энергия звезды за границей основной серии недостаточна, чтобы вызвать сильную флюоресценцию [тогда будет |H12(0)| < H'12(0) и H'12(0) ≈ H"12(0)]; однако это означает, что надо указать другой механизм (а не флюоресценцию) для объяснения ярких полос, наблюдающихся в спектрах новых звезд в это время; 2) в оболочке отсутствует лучевое равновесие (об этом см. ниже).
При нахождении светового давления, действующего на всю оболочку, Мс Сгеа [7] и Мустель [8] предполагали, что лоток внутри линии не меняется в оболочке (т. е. принимали модель Шустера). На самом деле надо учитывать как наличие градиента скорости, так и флюоресценцию. Соответствующие формулы могут быть легко даны с помощью результатов, полученных выше. Однако на этом мы не будем останавливаться.
г) Время релаксации
Для оболочек новых звезд важно установить "время релаксации", т. е. промежуток времени, необходимый для установления лучевого равновесия. Результаты теории лучевого равновесия можно применять только к тем оболочкам, продолжительность существования которых велика по сравнению с временем релаксации.
Можно считать, что время релаксации определяется продолжительностью нахождения светового кванта в оболочке. Поэтому для вычисления времени релаксации надо разделить число квантов, находящихся в оболочке, на число квантов, покидающих оболочку за единицу времени. Пользуясь формулами (32), для числа квантов, находящихся в столбе с сечением 1 см2, получаем
![$$
\frac{4\pi}{c}\int\limits_{r_1}^{r_2} (\bar K_{12} + \bar K_{13})dr = \frac{3}{\beta} \frac{\pi S_{13}}{ca_{13}} \left[q+\frac{\beta + \gamma}{3(1-p)}\right] .
$$](https://images.astronet.ru/pubd/2011/06/28/0001252608/tex/formula86.gif)
|
(84) |
Так как число квантов, уходящих из этого столба за 1 сек., очевидно, равно πS13, то для времени релаксации находим
|
|
(85) |
В начальной стадии оболочек новых звезд можно принять dv/dr ≈ v/r и β + γ ≈ q. В таком случае формула (77) дает для времени релаксации величину порядка нескольких часов.
Этот промежуток времени, конечно, очень мал для астрономических процессов. Однако в оболочках новых звезд, сразу после максимума блеска, происходят столь быстрые изменения, что предположение об отсутствии лучевого равновесия в это время не является неправдоподобным.
<< 4.3 Роль столкновений и общего поглощения в оболочке | Оглавление | Глава V. Звезды поздних спектральных классов с яркими линиями >>
|
Публикации с ключевыми словами:
оболочки звезд - перенос излучения
Публикации со словами: оболочки звезд - перенос излучения | |
|
См. также:
| |