2.1 Нижняя граница атмосферы
Чтобы применить ранее полученные результаты к звездной атмосфере, надо задать распределение плотноcтей и скоростей в атмосфере. В двух первых параграфах этой главы мы рассмотрим атмосферу, образованную материей, выбрасываемой из звезды с постоянной скоростью. Тогда плотность материи будет обратно пропорциональна квадрату радиуса. Рассмотрение такой модели является наиболее простым примером применения нашего метода, в изложении которого и состоит, собственно говоря, наша ближайшая цель. С другой стороны, такая модель весьма близко соответствует атмосферам звезд типов WR и Р Cygni, а также, в меньшей мере, атмосферам звезд типа Be. Поэтому результаты, полученные путем рассмотрения этой модели, будут достаточно надежно характеризовать (по крайней мере в качественном отношении) атмосферы указанных звезд.
Определим сначала нижнюю границу звездной атмосферы. Для этого необходимо знать, чем вызывается поглощение в непрерывном спектре в верхних слоях звезды. Легко доказать, что для рассматриваемых звезд это поглощение вызывается не фотоионизацией и гиперболическими переходами, а рассеянием света свободными электронами. Если это так, то радиус нижней границы атмосферы r0 определяется соотношением
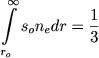
|
(1) |
где s0 - рассеивающая способность свободного электрона.
Мы уже условились считать, что плотность в атмосфере падает обратно пропорционально квадрату радиуса. Так как в атмосферах горячих звезд громадное большинство атомов. находится в ионизованном состоянии, то мы имеем
|
|
(2) |
где ne0 - число свободных электронов на нижней границе атмосферы. Подставляя (2) в (1), находим
|
|
(3) |
Такова связь между величинами r0 и ne0, если рассеяние света свободными электронами играет основную роль в поглощении в непрерывном спектре в наружных частях звезды.
Как уже сказано, последнее утверждение легко доказать. Для этого найдем оптическую толщину атмосферы за границей серии Лаймана. Мы имеем
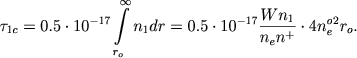
|
(4) |
Если принять, что радиус звезды в 10 раз больше радиуса Солнца (r0=7 ⋅ 1011), то из (3) находим ne0=7 ⋅ 1011. С этими значениями (r0 и ne0) из (4) получаем τ1c < 1 , если T∗=20000°; . При таких малых значениях величины τ1c оптическая толщина атмосферы в видимой части спектра, обусловленная фотоионизацией и гиперболическими переходами, будет порядка 0,001. Этим доказывается справедливость определения радиуса нижней границы атмосферы формулой (1).
При получении соотношения (4) мы считали, что в атмосфере звезды справедлива обычная ионизационная формула
|
|
(5) |
|
|
(6) |
|
|
(7) |
Так как для горячих звезд τ1c < 1, то справедливость этой формулы не вызывает сомнений. В противном случае необходимо было бы учитывать ослабление излучения, идущего от звезды, вследствие экстинкции, и наличие диффузного излучения атмосферы за границей лаймановской серии.
В дальнейшем мы везде будем считать, что τ1c < 1. Вследствие этого будет не только выполняться ионизационная формула (5), но будут также справедливыми численные результаты предыдущей главы, при получении которых принималось, что ионизация вызывается излучением, идущим непосредственно от звезды.
Легко получить также второе соотношение между величинами r0 и ne0. Для этого надо определить количество энергии, излучаемой атмосферой в какой-либо спектральной линии. Имея в виду использование численных результатов, полученных нами ранее для водородного атома, мы в этой главе будем говорить лишь об излучении атмосферы в бальмеровских линиях. Однако надо заметить, что подобные расчеты легко провести для любого атома. Пусть Hk - полная энергия, излучаемая атмосферой в k-й линии бальмеровской серии. Мы имеем
|
|
(8) |
где β2k - доля квантов, уходящих из атмосферы, вследствие эффекта Доплера, и интегрирование распространено по всему объему атмосферы. Эта формула может быть преобразована к виду
|
|
(9) |
где
|
|
(10) |
Но величина fk слабо зависит от параметра x. Например, при T=20000°; мы имеем:
| x | 0.01 | 0.1 | 1.0 |
| 1020f4 | 0.11 | 0.19 | 0.12 |
Поэтому величину fk можно вынести за знак интеграла. Считая, что ne=n+, вместо (9) получаем
|
|
(11) |
Это есть окончательная формула, определяющая величину Нk.
С другой стороны, величину Нk можно выразить через занстровскую величину Ak, получаемую из сравнения интенсивности линии и интенсивности соседнего участка непрерывного спектра звезды,
|
|
(12) |
Две последние формулы дают
|
|
(13) |
Мы получили новое соотношение [наряду с соотношением (3)], связывающее величины r0 и ne0. Соотношения (3) и (13) дают возможность определения величин r0 и ne0, т. е. радиуса нижней границы атмосферы и электронной плотности на этой границе. Во второе из этих соотношений, кроме величин r0 и ne0, входят занстровская величина Ak, получаемая из наблюдений, и температура звезды. Мы будем считать температуру звезды известной и для примера рассмотрим два случая: 1) T = 20000°; (звезды типов Р Cygni и Be) и 2) T=50000°; (звезды типа WR).
В первом из этих случаев мы можем взять: f4 = 0,15 ⋅ 10-20, А4 = 0,004 (среднее для многих звезд типа Be, по Mohler [1]), а во втором: f4 = 0,4 ⋅ 10-21, А4 = 0,002 (для звезды HD 192163, по данным Beals). Соотношения (3) и (13) для наших двух случаев дают: 1) ne0 = 3,6 ⋅ 1011, r0 = 1,4 ⋅ 1012 = 20r☉. 2) ne0 = 1,5 ⋅ 1012, r0 = 3,3 ⋅ 1011 = 5r☉.
Полученные значения величин r0 и ne0 представляются нам весьма правдоподобными. Для сравнения можно, например, отметить, что для двух затменных переменных звезд. типа WR были получены следующие значения радиуса: r0 = 5,8r☉ и r0 = 5,5r☉ (см. статью Gaposchkin [2]).
Пользуясь найденными значениями r0 и ne0, можно, между прочим, подсчитать количество материи, выбрасываемое звездой за год. Выбрасываемая масса, очевидно, равна
|
|
(14) |
где mH - масса водородного атома и v - скорость истечения материи. Эта формула дает: M ≈ 10-5M☉ для звезд типов WR и P Cygni и M ≈ 10-6M☉ - для звезд типа Be.
Надо заметить, что применение полученных формул ограничивается ненадежностью имеющихся значений звездных температур. Как известно, температуры звезд типа WR, определяемые методом Zanstra, оказываются тем более высокими, чем выше потенциал ионизации того элемента, по линиям которого температура определяется. Так, например, температуры, определенные по линиям водорода, ионизованного гелия и четыре раза ионизованного кислорода, оказываются порядка 20000°; , 60000°; и 100000°; соответственно. В значительной мере это расхождение вызывается сильным отклонением излучения звезды от излучения абсолютно черного тела, что в общих чертах объясняется теорией протяженных фотосфер. Можно указать также ряд других факторов, сказывающихся на определении температур методом Zanstra. Один из этих факторов состоит в том, что при высокой температуре звезды оптическая толщина атмосферы за границей основной серии атома с сравнительно низким потенциалом ионизации должна быть меньше единицы. Вследствие этого атмосфера будет поглощать лишь небольшую часть излучения звезды за границей основной серии данного атома, и температура, определенная по линиям этого атома, окажется заниженной. Как видно из формулы (4), так обстоит дело с водородом, если температура звезды больше 20000°; . Для этого случая с помощью формулы (4) метод Zanstra легко уточнить. Для этого левую часть уравнения Zanstra [см. уравнение (60) следующей главы] надо умножить на величину τ1c, взятую из формулы (4). Однако полученное таким образом соотношение будет слабо зависеть от температуры звезды, ибо с ростом температуры увеличивается число квантов за границей основной серии, но падает величина τ1c. Кроме того, в это соотношение войдет новая неизвестная величина - радиус звезды r0 [величина ne0 может быть исключена с помощью (3)]. Более точная связь такого же типа между T∗ и r0 (с учетом непрозрачности атмосферы для излучения в линиях и поглощения за границами субординатных серий) осуществляется вышеприведенной формулой (13).
<< Глава II. Звезды ранних классов с яркими линиями | Оглавление | 2.2 Изменение возбуждения вдоль радиуса >>
|
Публикации с ключевыми словами:
оболочки звезд - перенос излучения
Публикации со словами: оболочки звезд - перенос излучения | |
|
См. также:
| |