4.3 Роль столкновений и общего поглощения в оболочке
Наличие градиента скорости не является единственной причиной, ведущей к понижению степени возбуждения и ионизации атомов. Такое же влияние оказывают удары второго рода и общее поглощение в оболочке. Мы сейчас рассмотрим каждую из этих причин в отдельности.
а) Столкновения
При несоответствии между степенью возбуждения атомов и электронной температурой, столкновения между атомами и электронами ведут к уменьшению этого несоответствия. Если степень возбуждения ниже больцмановской при температуре электронного газа, то удары первого рода происходят чаще ударов второго рода и ведут к повышению степени возбуждения и понижению электронной температуры. При обратном положении чаще происходят удара второго рода, и это ведет к понижению степени возбуждения и повышению электронной температуры. В газовых туманностях осуществляется первый из этих случаев; в оболочках малого радиуса могут, по-видимому, осуществляться оба эти случая.
Допустим, что имеет место второй из указанных случаев, и выясним подробнее роль столкновений. Как и в § 1, возьмем атом с тремя уровнями. Для учета ударов второго рода мы должны в правой части перврго из уравнений (2) добавить член n2neD21. Тогда вместо первого из соотношений (14) получаем
|
|
(53) |
|
|
(54) |
Поэтому, переходя к уравнениям (22), мы вместо второго из этих уравнений находим
|
|
(55) |
|
|
(56) |
Мы видим, что влияние ударов второго рода формально сказывается так же, как наличие градиента скорости.
Для оценки величины δ мы можем воспользоваться формулой (III, 49), определяющей величины D1k для водородного атома. Так как
|
|
(57) |
то при T=10000°; (величина D21, впрочем, очень слабо зависит от T) мы находим
|
|
(58) |
Для звездных оболочек, рассмотренных нами в главе II, было получено β > 10-8, ne < 1012. Это значит, что в таких оболочках β >> δ, т. е. градиент скорости играет гораздо большую роль, чем удары второго рода. Для оболочек новых звезд положение является аналогичным.
б) Общее поглощение в оболочке
При наличии общего поглощения в оболочке уменьшение степени возбуждения и ионизации происходит как благодаря поглощению квантов, излучаемых данными атомами за границами серий, так и благодаря поглощению квантов, излучаемых в спектральных линиях. Чтобы рассмотреть этот эффект, надо добавить соответствующие члены к уравнениям переноса излучения, написанным выше. (Условия лучевого равновесия при этом, очевидно, не изменятся).
Возьмем снова атом с тремя уровнями. Вместо уравнений (16) и (18) мы теперь имеем
|
|
(59) |
|
|
(60) |
|
|
(61) |
а a'13 и a'12 - коэффициенты общего поглощения за границей основной серии и в спектральной линии.
Из уравнений (59) и (60) с помощью условий лучевого равновесия получаем
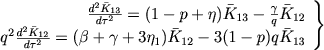
|
(62) |
[вместо уравнений (22)]. Характеристическое уравнение этой системы имеет вид
|
|
(63) |
и, если считать выполненным неравенство (26), то для λ1 находим
|
|
(64) |
Трудно сказать, не имея в виду конкретных оболочек и атомов, какой из членов, входящих в эту формулу, играет наибольшую роль. Отметим только, что в оболочках звезд поздних классов роль общего поглощения весьма значительна. Поэтому подробнее этот вопрос будет рассмотрен в следующей главе.
<< 4.2 Реальный атом | Оглавление | 4.4 Некоторые применения >>
|
Публикации с ключевыми словами:
оболочки звезд - перенос излучения
Публикации со словами: оболочки звезд - перенос излучения | |
|
См. также:
| |