4.2 Реальный атом
Рассмотрим теперь реальный атом, обладающий бесконечным числом уровней. Условие стационарности для i-го уровня имеет вид
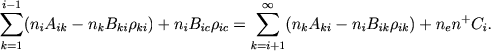
|
(39) |
Используя обозначения, введенные в предыдущем праграфе, мы можем написать
|
|
(40) |
Поэтому вместо (39) получаем
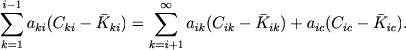
|
(41) |
К этим условиям лучевого равновесия надо присоединить еще уравнения переноса излучения. Для излучения в непрерывном спектре мы как всегда имеем
|
|
(42) |
а для излучения в спектральных линиях по аналогии с уравнением (18) предыдущего параграфа получаем
|
|
(43) |
|
|
(44) |
Система уравнений (41), (42) и (43) представляет громадные трудности для решения. Для неподвижной оболочки, т. е. при βik=0, эта система была рассмотрена В. А. Амбарцумяном [2] и Henyey [8]. При этом были получены несколько первых интегралов системы ("интегралы потока"). Легко видеть, что в рассматриваемом случае, т. е. при наличии градиента скорости, интегралы потока не существуют.
Однако наличие градиента скорости приводит к существенному упрощению вышеприведенной системы. Если градиент скорости достаточно велик, то для каждого элементарного объема в средних частях оболочки может считаться выполненным следующее условие: количество квантов, излучаемых в спектральной линии, равняется числу квантов, поглощаемых в этой линии, и числу квантов, уходящих из оболочки вследствие эффекта Доплера. В случае плоско-параллельных слоев это условие имеет вид
|
|
(45) |
То обстоятельство, что это условие действительно должно выполняться, вытекает из результатов, полученных в предыдущем параграфе. В самом деле, предполагая выполненным неравенство (25), мы получили, что в средних частях оболочки плотность излучения определяется формулами (32)(причем, как легко видеть, этот результат не зависит от граничных условий для излучения в линии). Но мы пришли бы к тем же самым формулам (32), если бы, наряду с уравнениями (14) и (16), рассмотрели не уравнение переноса (18), а соотношение (45) для частоты ν12. Это значит, что при выполнении неравенства (26) может считаться выполненным и соотношение (45).
Принимая соотношение (45) и считая, как и раньше, что оптическая толщина оболочки за границами субординатных серий меньше единицы (тогда величины ρ2c, ρ3c... будут заданными), мы видим, что задача состоит в сущности в том, чтобы найти плотность излучения за границей основной серии (ибо если все величины ρic известны, то нахождение степени возбуждения в каждом месте оболочки при наличии соотношения (45) представляет алгебраическую операцию). Конечно, на самом деле величина ρ1c сама зависит от степени возбуждения, но мы сейчас покажем, что для приближенного нахождения этой величины достаточно принять во внимание только два первых уровня.
Складывая почленно все уравнения (41), начиная со второго, получаем
|
|
(46) |
|
|
(47) |
|
|
(48) |
где qi=a1c/a1i. Кроме того, мы можем использовать соотношение (45) для линий основной серии. Тогда вместо (46) находим
|
|
(49) |
|
|
(50) |
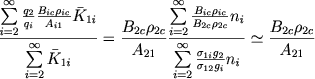
|
(51) |
(так как в обеих полученных суммах главную роль играют первые члены). Поэтому из (49) и (50) находим
|
|
(52) |
Полученное уравнение вместе с соответствующим уравнением переноса излучения (42) и решают задачу о ионизации в оболочке. Но легко видеть, что уравнение (52) мы получили бы, учитывая только два первых уровня. Следовательно, задача о возбуждении и ионизации реальных атомов действительно сводится к задаче, рассмотренной в предыдущем параграфе.
<< 4.1 Атом с тремя уровнями | Оглавление | 4.3 Роль столкновений и общего поглощения в оболочке >>
|
Публикации с ключевыми словами:
оболочки звезд - перенос излучения
Публикации со словами: оболочки звезд - перенос излучения | |
|
См. также:
| |