2. Основы сферической геометрии
Разделы
- 2.1. Основные понятия
- 2.2. Скаляры, векторы, тензоры и системы координат
- 2.3. Сферическая система координат
- 2.4. Основные формулы сферической геометрии
2.1. Основные понятия
Одним из главных достижений космического проекта HIPPARCOS,
осуществленного в 90-х годах XX века, является измерение
параллаксов (или расстояний) до
![]() звезд, которые
находятся на расстоянии до 1 килопарсека (кпк) от Солнца.
Несмотря на то, что объем, в котором расположены эти звезды
составляет очень малую часть от объема нашей Галактики, измерение
расстояний является важнейшим результатом проекта, потому что
оказалось возможным построить трехмерную картину ближайшей
окрестности Солнца.
звезд, которые
находятся на расстоянии до 1 килопарсека (кпк) от Солнца.
Несмотря на то, что объем, в котором расположены эти звезды
составляет очень малую часть от объема нашей Галактики, измерение
расстояний является важнейшим результатом проекта, потому что
оказалось возможным построить трехмерную картину ближайшей
окрестности Солнца.
Если расстояния до небесных объектов неизвестны, то удобно отнести все объекты: звезды, радиоисточники и т.д. на одно и то же расстояние, то есть расположить их на поверхности сферы с центром в точке, где находится наблюдатель. Такая сфера называется небесной сферой. Радиус небесной сферы произволен, но удобно для дальнейших вычислений считать его равным единице.
Чтобы знать изменение положения звезды в пространстве, необходимо измерить три компоненты скорости звезды. К сожалению для большинства звезд известны лишь две компоненты скорости в картинной плоскости, то есть в плоскости, перпендикулярной линии, соединяющей наблюдателя и звезду. Удобнее всего считать, что картинная плоскость совпадает с плоскостью, касательной к небесной сфере.
Геометрические построения и вычисления на поверхности сферы отличаются от таковых на плоскости. Поэтому можно говорить о сферической геометрии как о самостоятельном разделе геометрии. Следует заметить, что формулы сферической геометрии справедливы не только для небесной сферы, но и для любой другой сферы (например, при проведении вычислений на земном глобусе). Необходимо лишь учитывать радиус сферы.
Одними из основных понятий планиметрии являются понятия точки и прямой линии. В сферической геометрии аналогом прямой линии как линии с наименьшей длиной, соединяющей две точки, является дуга окружности, образованной пересечением большого круга с небесной сферой. Так как круг -- это часть плоскости, ограниченная окружностью, то дадим следующее определение.
Через любые две точки, лежащие на поверхности сферы, можно провести большой круг. Это утверждение эквивалентно аксиоме из планиметрии: через любые две точки можно провести прямую линию. Перпендикуляр к большому кругу, проходящий через центр сферы, пересекает ее в двух точках, называемых полюсами. Большой круг пересекает сферу по окружности. Очевидно, что любая прямая, лежащая в плоскости большого круга и проходящая через центр сферы, является диаметром сферы. Следовательно, два больших круга пересекаются по диаметру сферы.
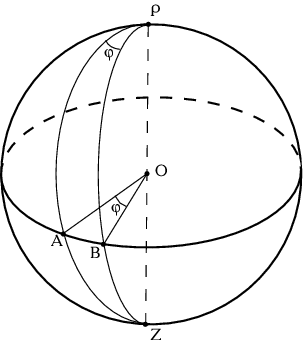
Рассмотрим сферу с центром в точке ![]() (рис. 2.1).
(рис. 2.1).
Проведем большой круг через две точки ![]() и
и ![]() , лежащие на
поверхности сферы, затем проведем перпендикуляр к большому кругу.
Полюсы обозначим как
, лежащие на
поверхности сферы, затем проведем перпендикуляр к большому кругу.
Полюсы обозначим как ![]() и
и ![]() . Через точки
. Через точки ![]() и
и ![]() , затем
через
, затем
через ![]() и
и ![]() проведем два больших круга.
проведем два больших круга.
Единицами измерения углов в астрономии являются градусы, радианы,
часы. Так как радиус сферы равен единице, то длина дуги
![]() (рис. 2.1) равна центральному углу
(рис. 2.1) равна центральному углу ![]() ,
то есть
,
то есть ![]() , выраженному в радианах. По определению градус
, выраженному в радианах. По определению градус
![]() -- это центральный угол, равный
-- это центральный угол, равный ![]() части
окружности. Градус делится на 60 угловых минут
части
окружности. Градус делится на 60 угловых минут
![]() ,
каждая из которых равна 60 угловым секундам
,
каждая из которых равна 60 угловым секундам
![]() , то
есть градус состоит из 3600 угловых секунд
, то
есть градус состоит из 3600 угловых секунд
![]() .
.
Длина окружности равна ![]() радиан, поэтому
радиан, поэтому
В современных астрометрических наблюдениях точность намного
превышает
![]() . Поэтому часто в качестве единицы измерения
углов используется миллисекунда (мс) дуги, причем
. Поэтому часто в качестве единицы измерения
углов используется миллисекунда (мс) дуги, причем
![]() мс
дуги
мс
дуги![]() . Чтобы представить себе величину угла в 1 мс
дуги, вычислим угловой размер горошины диаметром 5 мм,
находящейся на расстоянии, равном 1000 км. Угловой размер
горошины равен:
. Чтобы представить себе величину угла в 1 мс
дуги, вычислим угловой размер горошины диаметром 5 мм,
находящейся на расстоянии, равном 1000 км. Угловой размер
горошины равен:
Для измерения углов используются также часы, причем ![]() -- это центральный угол, соответствующий
-- это центральный угол, соответствующий ![]() части
окружности. В одном часе содержится 60 минут или 3600 секунд
части
окружности. В одном часе содержится 60 минут или 3600 секунд
![]() . Очевидно, что
. Очевидно, что
![]() .
.
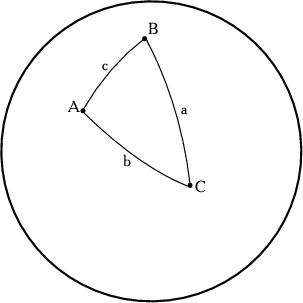
Рассмотрим теперь три точки, которые лежат на сфере и не принадлежат одному большому кругу. Через каждую пару точек можно провести большие круги (рис. 2.2).
Обычно углы сферического треугольника обозначают большими
буквами, например ![]() , а стороны, противолежащие углам
-- соответствующими малыми буквами:
, а стороны, противолежащие углам
-- соответствующими малыми буквами:
![]() (рис. 2.2). Как и в планиметрии, в сферической геометрии
существуют определенные соотношения между сторонами и углами
треугольников. Основные формулы, связывающие углы и стороны
треугольника, будут выведены в следующем параграфе. Здесь отметим
лишь следующие свойства сферических треугольников. Углы
(рис. 2.2). Как и в планиметрии, в сферической геометрии
существуют определенные соотношения между сторонами и углами
треугольников. Основные формулы, связывающие углы и стороны
треугольника, будут выведены в следующем параграфе. Здесь отметим
лишь следующие свойства сферических треугольников. Углы ![]() и
и ![]() в треугольнике
в треугольнике ![]() (рис. 2.1) - прямые, так как большие
круги, проходящие через точки
(рис. 2.1) - прямые, так как большие
круги, проходящие через точки ![]() и
и ![]() , перпендикулярны
плоскости
, перпендикулярны
плоскости ![]() . Поэтому, поскольку угол
. Поэтому, поскольку угол ![]() , сумма углов
сферического треугольника может превышать
, сумма углов
сферического треугольника может превышать ![]() . Теперь
проведем плоскость через точки
. Теперь
проведем плоскость через точки ![]() (рис. 2.2), лежащие
на сфере, и параллельно ей плоскость, которая проходит через центр
сферы. Очевидно, что эта плоскость поделит сферу на две полусферы,
причем треугольник
(рис. 2.2), лежащие
на сфере, и параллельно ей плоскость, которая проходит через центр
сферы. Очевидно, что эта плоскость поделит сферу на две полусферы,
причем треугольник ![]() будет полностью лежать в одной из
полусфер. Таким образом, любой из углов сферического треугольника
будет меньше, чем
будет полностью лежать в одной из
полусфер. Таким образом, любой из углов сферического треугольника
будет меньше, чем ![]() . В пределе (при увеличении каждого
из углов до
. В пределе (при увеличении каждого
из углов до ![]() ) сферический треугольник трансформируется
в полусферу.
) сферический треугольник трансформируется
в полусферу.
Следующие свойства сферического
треугольника аналогичны свойствам плоского треугольника:
а) В каждом сферическом треугольнике против
большего угла лежит большая сторона;
б) Сумма любых двух сторон больше третьей стороны.
Найдем площадь сферического треугольника. Для этого рассмотрим
треугольник ![]() (рис. 2.3).
(рис. 2.3).
Определим теперь площадь всей небесной сферы. Для этого удобно площадь
сферы выразить в квадратных градусах. Для этого сначала выразим радиус
сферы в градусах:
![]() . Тогда площадь всей сферы равна
. Тогда площадь всей сферы равна
<< 1.2. Краткий исторический обзор | Оглавление | 2.2. Скаляры, векторы, тензоры >>
|
Публикации с ключевыми словами:
астрометрия - сферическая астрономия - системы координат - шкалы времени
Публикации со словами: астрометрия - сферическая астрономия - системы координат - шкалы времени | |
См. также:
Все публикации на ту же тему >> | |