Глава VIII. Применение анализа размерностей к задачам космологии
§ 8.1 Структура квазаров и ядер галактик
Процессы, протекающие в квазарах и ядрах галактик, представляют собой одну из самых больших загадок в астрофизике. В самом деле, многие открытия последних лет были поняты в рамках известных физических законов. Пульсары были отождествлены с давно предсказанными нейтронными звездами; реликтовое излучение, как следствие модели "горячей Вселенной", было ранее рассчитано теоретически; линии "мистериума" в радиодиапазоне были отождествлены с космическим мазером и т.д. Вместе с тем, наше понимание природы квазаров и ядер галактик не намного расширилось со времени первого теоретического "бума", последовавшего за открытием квазаров в 1963 г.
Характерными деталями оптических спектров квазаров и ядер галактик являются эмиссионные линии, имеющие сложную структуру и необычайную ширину, порой достигающую сотни ангстрем. Спектроскопические наблюдения позволяют определить параметры области, в которой образуются указанные линии, и построить ее геометрическую модель. Внутренние, наиболее плотные части газовой оболочки имеют плотности порядка 107 см-3 и размеры около парсека (1018 см). Наружные части простираются до десятков и сотен парсек, постепенно переходя в межзвездный газ окружающей галактики. Квазары, по-видимому, также являются ядрами галактик, но гигантских эллиптических, а не спиральных, известных под названием галактик Сейферта. Данные о физических параметрах для ряда квазаров и родственных объектов приведены в табл. 14.
| Объект | Оптическая светимость, эрг/сек |
Масса газа, M☉ |
Эффективная скорость, км/сек |
Кинетическая энергия газа, эрг |
Масса центрального тела, M☉ |
|
| Квазары | ЗС-273 | 1046 | 106 | ± 3500 | 1056 | 2 ⋅ 109 |
| ЗС-48 | 1045 | 105 | ± 1000 | 1055 | 109 | |
| N-галактики | Тонанцитла 256 | 3 ⋅ 1044 | 3 ⋅ 104 | ± 1500 | 5 ⋅ 1054 | 3 ⋅ 108 |
| ЗС-120 | 1044 | 103 | ± 3000 | 3 ⋅ 1053 | 108 | |
| Галактики Сейферта |
Маркарян 79 | 3 ⋅ 1043 | 104 | ± 2500 | 5 ⋅ 1053 | 5 ⋅ 107 |
| NGC 4151 | 1043 | 103 | ± 2500 | 5 ⋅ 1052 | 5 ⋅ 107 | |
| NGC 1275 | 1043 | 103 | ± 1500 | 1052 | 5 ⋅ 107 | |
| NGC 4051 | 1041 | 102 | ± 1000 | 1050 | 106 | |
Первым отличительным свойством квазаров и ядер галактик является большая концентрация энергии в относительно небольшом объеме. Вторым важным свойством является большая кинетическая энергия газа, на много порядков превосходящая энергию взрыва сверхновых звезд. Третье, весьма экзотическое свойство, - переменность блеска квазаров и ядер галактик.
На рис. 40 воспроизводится кривая блеска одного из наиболее изученных объектов этого класса - сейфертовской галактики NGC 4151 [1]. Поскольку характерное время наименьшего периода не превосходит нескольких месяцев и даже недель, соответственно можно оценить и характерный размер излучающих элементов - не более 1016-1017 см. Имеются аргументы, указывающие на то, что главное тело квазара находится внутри газовой оболочки.
Физические свойства собственно ядра квазара неясны. Исторически первой гипотезой в этом направлении была гипотеза Хойла - Фаулера о гравитационном коллапсе массивного тела. Рассматривались также варианты скопления нейтронных звезд, магнито-турбулентного образования, гигантского квазипульсара с быстрым вращением, "черной дыры" в центре галактики и т.д. (подробности см, в [2]). Мы не будем рассматривать здесь эти модели. Приведем результаты анализа свойств квазаров согласно интересной работе Дайсона [3].
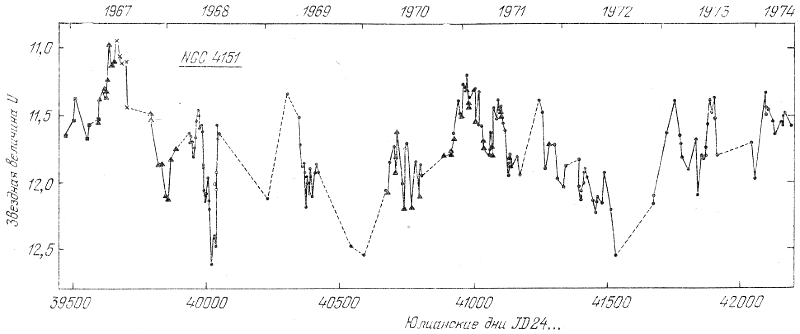
Рис. 40. Кривая блеска ядра сейфертовской галактики NGC 4151 [1].
Удобно ввести величину характерного числа частиц в звезде
|
|
(8.1) |
Считаем, что область радиуса R имеет оптическую толщу порядка единицы
|
|
(8.2) |
где σ - коэффициент томсоновского рассеяния. Предполагая, что при коллапсе масса оболочки, сравнимая с массой звезды, "распылилась" по всей области, имеем
|
|
откуда
|
|
(8.3) |
Вспоминая, что R=ct и выражая коэффициент томсоновского рассеяния через мировые постоянные, найдем выражение для характерного времени всплеска:
|
|
(8.4) |
Для электронной плотности в области высвечивания имеем
|
|
(8.5) |
Для определения температуры будем исходить из условия равенства плотности кинетической и лучистой энергий. Плотность кинетической энергии есть
|
|
(8.6) |
а плотность лучистой энергии, как известно,
|
|
(8.7) |
Сравнивая (8.6) и (8.7), найдем температуру излучения
|
|
(8.8) |
Осталось вывести формулу для светимости. Полагая, что энергия высвечивается за характерное врем t согласно (8.4), получим
|
|
(8.9) |
Выразим все формулы через мировые постоянные и величину N. Поскольку значения постоянных извести (см. приложение II), aN ≈ 4 ⋅ 1057, то получаем:
- характерное время пульсаций блеска
- характерный размер области высвечивания
- электронная плотность
- температура излучения
- интегральная светимость
|
|
|
|
|
|
|
|
|
|
|
|
В принципе, весьма информативными являются наблюдения переменности блеска квазаров и ядер галактик. Если ядро квазара - скопление звезд, то изменения блеска будут носить характер случайных флуктуации. Если, наоборот, кривая блеска периодическая, необходимо рассматривать вращающуюся модель наподобие пульсара. Существующий наблюдательный материал основан на фотографических измерениях, и получаемые выводы спорны. Более точные фотоэлектрические наблюдения начаты относительно недавно. Пока можно сделать предварительный вывод, что изменения блеска квазаров не являются строго периодическими, но в то же время их нельзя считать чисто случайными.
Приведем также оценки масс центрального тела квазара или ядра галактики, полученные несколькими способами по формулам, приведенным в этой книге. Во-первых, можно использовать теорию сильного взрыва, предполагая подобие квазаров и сверхновых. Кинетическая энергия взрыва сверхновой первого типа с массой порядка солнечной массы составляет 1048 - 1049 эрг. Считая процессы в сверхновых и квазарах подобными, получим, что при кинетической энергии газа в ЗС-273, равной 1055 эрг, необходим взрыв тела с массой 107 масс Солнца. Для галактики NGC 4051 получаем массу 100 солнечных. Если не вся масса центрального тела взрывается, эти оценки дают заниженное значение массы.
Второй способ основан на определении массы по светимости в предположении, что светимость близка к критической [2]. Поскольку критическая светимость для одной солнечной массы составляет ∼ 1038 эрг/сек, получаем для ЗС-273 оценку массы 108-109 масс Солнца, для NGC 4051 - около 103 масс Солнца. И здесь получается заниженная масса, поскольку реальная светимость квазаров и ядер галактик, скорее всего, ниже критической. Еще один способ заключается в изучении кривой вращения галактики, содержащей квазар или сейфертовское ядро. Эту возможность не всегда удается реализовать ввиду целого ряда специфических условий (наличие эмиссий газа, подходящий угол наклона, достаточный угловой размер и т. д.). Однако в этом случае можно дать динамическую оценку массы, заключенной внутри некоторого радиуса. Для одной из сейфертовских галактик NGC 1068 такая оценка приводит к пределу М ≲ 108 масс Солнца.
Наконец оценка массы центрального тела возможна, если предположить, что наблюдаемые скорости газа равны по порядку величины параболической скорости, или скорости убегания. Величина скорости определяется по ширинам эмиссионных линий, величину характерного размера излучающей области можно определить, зная плотность, температуру и светимость газа. Оценки массы приведены в последнем, столбце табл. 14. Если такое предположение о скоростях газа справедливо, оно позволяет довольно естественно объяснить феномен широких эмиссий, наблюдаемых в квазарах и ядрах галактик.
Проблема определения масс квазаров и ядер галактик является важной, в частности, и в связи с предполагаемым наличием в центрах галактик гипотетических "черных дыр" [4, 5]. В ряде работ [6-8] обсуждаются следствия, вытекающие из подобия процессов в окрестностях "черных дыр" в широком интервале масс. Вспомним формулу (3.54) для светимости при аккреции на релятивистский объект
|
|
Для рентгеновского источника Лебедь Х-1 с массой 10 солнечных и светимостью около 1038 эрг/сек необходимый приток массы
|
|
Для квазара или ядра галактики с ожидаемой массой порядка 108 M☉ для поддержания излучения требуется
|
|
при 100%-ной переработке энергии падающего вещества в излучение. Поскольку выход энергии при сферически-симметричной аккреции составляет несколько процентов Мс2, эта цифра должна быть соответственно увеличена. Ясно, что при таких относительно скромных требованиях в галактике с массой 1010-1011 M☉ возможна активность ядра в течение долгого времени, сравнимого с временем жизни галактики.
Далее, можно записать выражение для минимального времени флуктуации блеска при падении вещества на "черную дыру":
|
|
(8.10) |
что при M=108 M☉ дает нижний предел времени изменения блеска порядка нескольких часов. Реальная цифра должна быть увеличена на фактор 10-30, поскольку процессы излучения происходят на некотором расстоянии от гравитационного радиуса.
Наконец можно оценить температуру равновесного излучения (формула (3.58)):
|
|
Заменяя L через выражение для эддингтоновской светимости, a R - через выражение для гравитационного радиуса, имеем
![$$
T \approx \sqrt[4]{\frac{c^5 m_p}{G\sigma M \sigma_T}} \approx 10^{7,5} \left(\frac{M}{M_\odot}\right)^{1/4} \, \mbox{град}.
$$](https://images.astronet.ru/pubd/2013/03/01/0001281314/tex/formula762.gif)
|
(8.11) |
Если при М = 1M☉ максимум излучения приходится па рентгеновский диапазон, то при M ≈ 108 M☉ темпера тура равна ≈ 105 K, и максимум сдвигается в ультрафиолет.
В настоящее время трудно судить о реальности какой-либо из предложенных моделей ядер галактик й квазаров. Наблюдения свидетельствуют о том, что, вероятно, параметры ядер связаны с массами и, возможно, структурой окружающей галактики. Можно ввести безразмерный параметр отношения светимостей ядра и галактики [9], который, по-видимому, изменяется с морфологическим типом галактики. Этот параметр порядка нескольких процентов для спиральных сейфер-товских галактик, около 50% для N-галактик, а у квазаров излучение ядра подавляет излучение возможной галактики, окружающей квазар (некоторые близкие квазары обнаруживают наличие такой галактики). Представляет интерес поиск второго безразмерного параметра, характеризующего структуру галактики и коррелирующего с отношением светимостей. Не исключено, что таким параметром могло бы быть отношение центральной и средней плотностей галактик (один из основных параметров классификации галактик по Моргану). Исследования галактик с высоким градиентом поверхностей яркости (и соответственно, плотности) показывают, что среди них действительно обнаруживаются галактики с сейфертовскйми ядрами в количестве, превышающем частоту встречаемости сейфертовских объектов среди галактик поля.
<< § 7.5 Численное моделирование плоских вращающих галактик | Оглавление | § 8.2 Гравитационная неустойчивость >>