§ 7.5 Численное моделирование плоских вращающихся галактик
Для численного моделирования систем, состоящих из 1010 - 1012 звезд, необходимо решать системы типа (7.1) для очень большого числа тел, как, например, N ≈ 104 - 105. Разумеется, прямое численное интегрирование (7.1) с помощью современных ЭВМ для этого случая пока невозможно. Поэтому используется другой метод, который мы сейчас и опишем.
Выразим ускорение i-й звезды через величину потенциала всей звездной системы в точке нахождения этой звезды
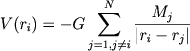
|
(7.73) |
Уравнения движения будут иметь вид
|
|
(7.74) |
Последовательность вычислений в этом методе заключается в следующем. Разобьем пространство на сетку ячеек и зададимся некоторым распределением звезд в этом пространстве. По этому распределению вычислим значения потенциалов в каждой ячейке (например, в центрах). Затем, в соответствии с уравнением (7.74), вычислим ускорение данной звезды, что позволит определить скорость и новое положение каждой звезды через один шаг по времени. Получаем новое распределение звезд в пространстве. Затем снова вычисляем потенциал по новому распределению звезд, опять находим ускорение всех звезд и т. д. Трудностей с учетом звездных сближений здесь нет благодаря тому, что, вычисляя Потенциал в центрах каждой ячейки, мы учитываем только вклад от тех звезд, которые расположены в других ячейках. Суммирование при вычислении потенциала по 'большому числу звезд также может быть упрощено, если отнести положение всех звезд, оказавшихся в данной ячейке, к ее центру. Наконец и расчет движения звезд может быть упрощен тем, что можно считать перемещения дискретными, происходящими путем переходов из центра одной ячейки в центр другой ячейки. Поэтому таким методом удается при затрате относительно небольшого машинного времени рассчитать звездные системы, состоящие из сотен тысяч звезд.
Для вычисления потенциала можно использовать преобразование Фурье - это в несколько раз ускоряет счет, хотя и требует большей машинной памяти. Пока этот метод применялся для моделирования плоских (двумерных) звездных систем, имитирующих спиральные галактики. Целью таких численных экспериментов и было выяснение вопроса о неустойчивости плоских вращающихся звездных дисков, о возможном появлении здесь спиральной структуры.
В плоской звездной системе потенциал выражается через поверхностную плотность звезд ρ(s)(x, y)
|
|
(7.75) |
Разбивая плоскость звездного диска на сетку с квадратными ячейками (число ячеек обозначим через N1 × N2) и считая, что теперь ρ(s)ik означает число звезд единичной массы в ячейке с номерами i и k по осям координат, имеем для потенциала в ячейке
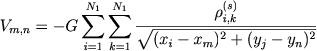
|
(7.76) |
где xm и yn - координаты центров ячеек. Компоненты ускорения в центрах ячеек:
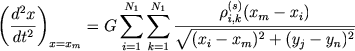
|
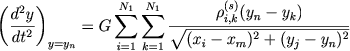
|
(7.77) |
Можно определять ускорение звезд и по разности потенциалов в соседних ячейках, используя подходящие интерполяционные формулы.
Для сокращения времени численного счета удобно воспользоваться преобразованием Фурье. Для этого следует перейти в (7.76) к целочисленным координатам, выбирая за единицу длины сторону ячейки. Тогда запишем (7.76) в безразмерном виде:
|
|
(7.78) |
где ρi, k(s) - полная масса звезд в ячейке с координатами xi = ia yk = ka, а Hij есть функция Грина для ньютоновского потенциала:
|
|
(7.79) |
Преобразование Фурье освобождает нас от двухкратного суммирования в (7.78), заменяя эту формулу на простое соотношение
|
|
(7.80) |
куда входят фурье-образы соответствующих величин, а именно
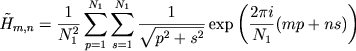
|
(7.81) |
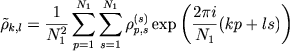
|
(7.82) |
и аналогично для ![]() . Фурье-образ функции Грина (7.81) хранится в памяти ЭВМ, а для вычисления
. Фурье-образ функции Грина (7.81) хранится в памяти ЭВМ, а для вычисления ![]() и обратного преобразования Фурье для определения Vm, n по
и обратного преобразования Фурье для определения Vm, n по ![]() , п, найденного из (7.80), существуют стандартные программы. Именно по этой методике, хотя и различающейся в деталях, проводилось численное моделирование плоских вращающихся галактик.
, п, найденного из (7.80), существуют стандартные программы. Именно по этой методике, хотя и различающейся в деталях, проводилось численное моделирование плоских вращающихся галактик.
Серию численных экспериментов по исследованию устойчивости вращающегося плоского диска провели Холь и Хокней [31-34]. Модели, принятые в этой серии исследований, состояли из 50000 или 200000 звезд, находящихся в плоскости диска. Диск был разделен на сетку из 64 × 64 или 128 × 128 ячеек (в разных вариантах). В соответствии с описанным выше методом определялся потенциал в центрах ячеек при помощи преобразования Фурье и рассчитывалось движение звезд по двойным интерполяционным формулам, учитывающим значение потенциала в четырех соседних ячейках. Находилось новое распределение плотности и вычисление потенциала повторялось. Шаг по времени выбирался так, что диск звезд совершал полный оборот за 200 или 400 шагов по времени. Оказалось, что характер эволюции модели слабо зависит от выбора числа ячеек, числа звезд или величины шага по времени в указанных выше пределах. Подробно метод, примененный Холем и Хокней, описан в работе [32]
Результаты численного эксперимента можно суммировать следующим образом. В работе [34] изучалась устойчивость звездного диска в зависимости от выбора дисперсии скоростей звезд в предположении, что вращение диска имеет твердотельный характер, т. е. происходит с постоянной угловой скоростью по крайней мере в начальный момент времени. Твердотельное вращение имеет место, если распределение поверхностной плотности звезд описывается формулой:
|
|
(7.83) |
Угловая скорость вращения выражается через плотность в центре диска ρ0(s) формулой
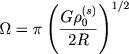
|
(7.84) |
где R - полный радиус диска. Рассматривалось несколько вариантов, отличающихся друг от друга разным заданием начальной дисперсии скоростей звезд, причем считалось, что в начальный момент дисперсия скоростей звезд в данном месте составляет определенный процент от квадрата линейной скорости вращения диска в том же месте.
На рис. 31 показана эволюция диска звезд, полученная в этих моделях для случая, когда начальной дисперсии скоростей нет вообще. Время выражено в периодах вращения. Видно, что уже за одну треть оборота в диске образовались четко выраженные сгущения и к концу одного оборота диск полностью распался, в полном согласии с результатами Тумре (см. § 2 этой главы и [11]), т. е. вращающийся плоский диск галактики неустойчив для возмущений с малой длиной волны. Затем на рис. 32-35 показана эволюция вращающегося диска при дисперсии скоростей 6,8; 13,6; 20,4 и 27,2 % соответственно от круговой скорости. Видно, как с увеличением дисперсии скоростей диск становится все менее подверженным распаду на сгущения и в последнем случае оказался устойчивым, также в полном согласии с теоретическими выводами, т. е. с соотношением (7.52) или (7.53).
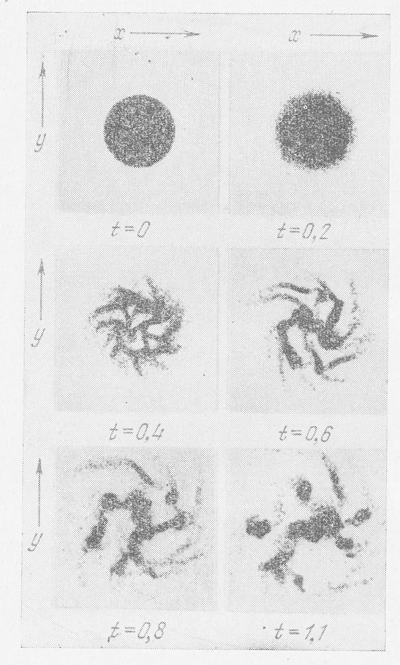
Рис. 31. Эволюция вращающегося диска звезд, в котором начальная дисперсия скоростей звезд равна нулю..
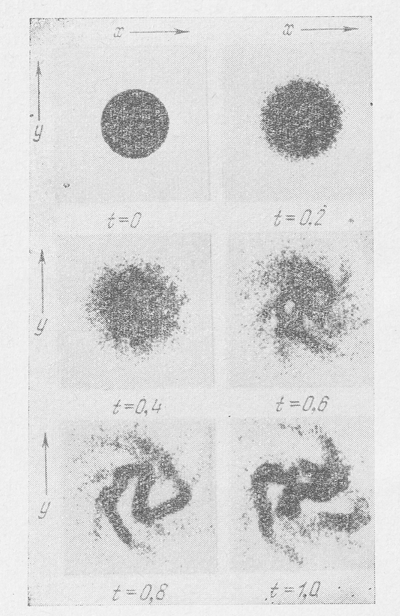
Рис. 32. То же, что и на Рис. 31, но с начальной дисперсией скоростей, равной 6.8 % от круговой скорости на краю диска...
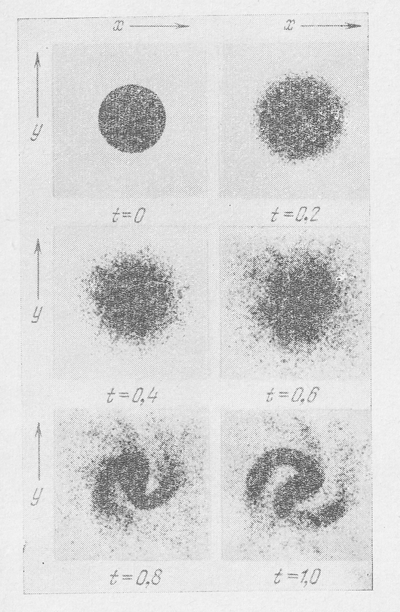
Рис. 33. То же, что и на Рис. 31, но с начальной дисперсией скоростей, равной 13.6 % от круговой скорости на краю диска...
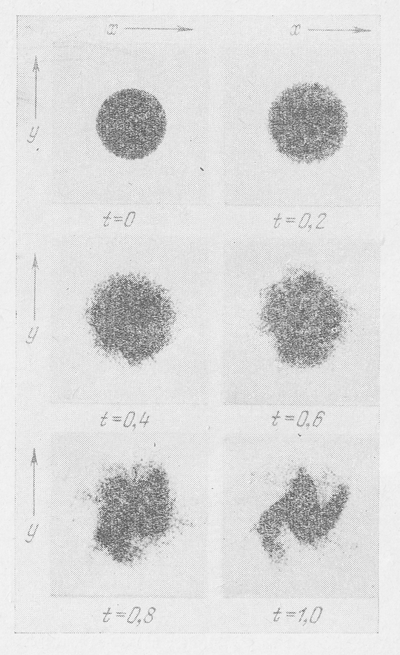
Рис. 34. То же, что и на Рис. 31, но с начальной дисперсией скоростей, равной 20.4 % от круговой скорости на краю диска...
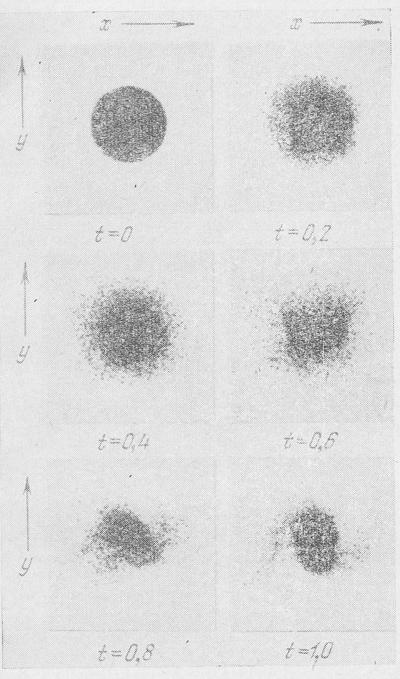
Рис. 35. То же, что и на Рис. 31, но с начальной дисперсией скоростей, равной 27.2 % от круговой скорости на краю диска. В этом случае критерий неустойчивости Тумре удовлетворяется...
В работе [32] рассматривались подобные же модели, но было принято другое распределение поверхностной плотности. Изучалось гауссово ρ(s) ∼ exp (-const r2) и экспоненциальное ρ(s) ∼ exp (-const r) распределения поверхностной плотности. Картина в общем аналогична. Без дисперсии скоростей звезд или при малой дисперсии диск оказывается неустойчивым, а введение достаточно большой дисперсии скоростей ста'билизирует диск.
Правильные спиральные рукава получались в этих моделях только для случая, когда в системе имелось заметное центральное уплотнение, в котором сосредоточена большая часть массы галактики. Одно и то же звездное уплотнение можно было проследить в течение восьми оборотов.
В работе [32] изучалась также пучковая неустойчивость гравитационных систем. Допустим, что два потока звезд с одинаковой звездной плотностью и одинаковой дисперсией скоростей vI, проникают друг через друга, двигаясь с относительной скоростью vR. Тогда, как известно из теории, оба потока должны распасться на отдельные сгущения и прекратить свое существование, если только относительная скорость потоков меньше дисперсии скоростей звезд в каждом потоке, т. е. если vR < vI
Численный эксперимент показал, что действительно при -малой относительной скорости потоков система звезд распадается на отдельные сгущения.
При больших относительных скоростях, т. е. при больших значениях vR / vI, неустойчивость также проявляется, но у нее теперь другой вид - вместо отдельных беспорядочных сгущений появляется нечто вроде волокнистой структуры, вытянутой вдоль оси движения потоков.
Любопытно напомнить, что открытие асимметрии дисперсия скоростей звезд еще в конце прошлого века привело к появлению двух представлений о движении звезд в Галактике. Согласно одному из них, теперь общепринятому, имеется центроид звезд, обращающийся вокруг центра Галактики, и по отношению к этому центроиду пекулярные скорости звезд распределены согласно неизотропному, эллипсоидальному шварцшильдовскому распределению. Согласно другому представлению, ранее очень популярному, в Галактике имеется два взаимопроникающих потока звезд, и наблюдаемая функция распределения скоростей соответствует наложению двух максвелловских распределений. Теперь ясно, что такая система неустойчива и должна распасться.
Еще одно замечание по этому поводу. Часто рассматривалось "столкновение" галактик и при этом утверждалось, что в силу того, что звездная плотность очень мала, две столкнувшиеся галактики пройдут друг через друга почти без возмущений, если только не учитывять взаимодействие межзвездной среды в этих галактиках. Теперь мы знаем, что эффект пучковой неустойчивости приведет к полному разрушению обеих столкнувшихся галактик, даже если их звездная плотность и очень мала, а межзвездного газа нет совсем.
Вторая группа исследователей, занимавшаяся плоскими звездными системами, основное внимание уделила моделированию спиральных рукавов в диске Галактики [35-38]. Модель строилась следующим образом. Плоскость диска разбивалась сеткой на 256 × 256 ячеек (в наиболее полной модели). В отличие от предыдущей группы исследователей, здесь и пространство скоростей разбивалось на дискретные ячейки (всего 63 × 63 ячейки), причем движение звезд рассматривалось как переходы между центрами всех ячеек согласно определенным правилам "игры", учитывающей движение частиц под действием гравитационного потенциала. Как и ранее, гравитационный потенциал определялся методом фурье-преобразовалия по заданному или определенному в процессе счета распределению поверхностной плотности. В наиболее полной модели было 115659 материальных точек, которые все имели одинаковую массу.
Метод численного моделирования здесь такой же, как описанный выше. В первых же расчетах авторы получили очень быстрое нагревание звездной системы. Дисперсия скоростей быстро увеличивалась, сами звезды распределялись по большому объему в плоскости диска, образуя быстро вращающееся плотное ядро и распределенное гало. Никакой спиральной структуры в такой системе не появлялось.
Поэтому авторы пришли к выводу, что для того, чтобы смоделировать образование спиральных рукавов в звездной системе с произвольным, например, однородным распределением звездной плотности, необходимо как бы "охлаждать" систему, уменьшать дисперсию скоростей материальных точек.
Для этого была рассмотрена следующая модель. Предполагалось, что система состоит из звезд и газовых облаков. И те и другие движутся в поле гравитационного потенциала, рассчитанного по распределению полной плотности в соответствии с действующими на них ньютоновскими силами. Но при рассмотрении движения газовых облаков учитывалась еще одна особенность. Если в процессе движений в одной пространственной ячейке окажутся два или несколько газовых облаков одновременно (но при этом они распределены по разным ячейкам пространства скоростей), то считается, что облака здесь неупруго сталкиваются и теряют свою анергию. Иными словами, скорости облаков после этого шага вычисляются с условием сохранения импульса и момента импульса, но с потерей энергии на внутренние степени свободы облака (предполагается, что эта энергия затем высвечивается). Этот эффект приводит к существенному охлаждению системы.
Учитывалась также возможность превращения газовых облаков в звезды. Предполагалось, что число вновь образовавшихся звезд в данной фазовой ячейке пропорционально квадрату числа газовых облаков в этой ячейке. Коэффициент пропорциональности выбирался малым, от 1/1000 до 1/500. Как пример, отметим, что в наиболее полном расчете из 115659 газовых облаков в конце концов образовалось 99523 звезды.
Задавалась также начальная скорость вращения диска, которая выбиралась либо из условия баланса между центробежной силой и гравитационным притяжением, либо считалось, что центробежная сила в два раза меньше гравитационной (чтобы получить более быстрый эффект гравитационной эволюции).
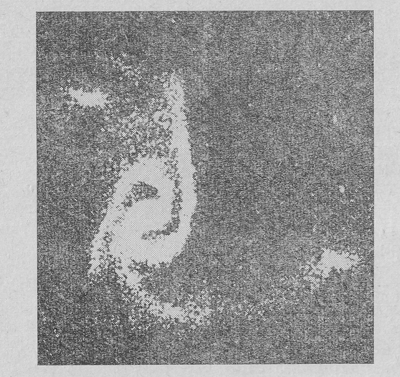
Рис. 36. Численное моделирование образования спиральных рукавов (кадры из фильма) .
Было проведено несколько расчетов, из которых один дал наиболее полные результаты. Последовательность положений звезд и газовых облаков в такой численной модели была смонтирована в виде фильма, который очень наглядно показывает эволюцию вращающегося звездно-газового диска. Кадры из этого фильма приведены на рис. 36, 37. Качественно картины согласуются, хотя надо отметить следующее существенное обстоятельство - в численном расчете ни один спиральный рукав не сохранялся больше трех оборотов, в то время как в реальных галактиках спиральные рукава сохраняются гораздо дольше.
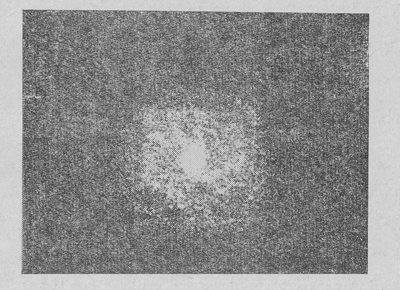
Рис. 37. Численное моделирование образования спиральных рукавов (кадры из фильма) .
Кроме того, в численной модели спиральную структуру показывают только точки, имитирующие "газовые облака". Звездный фон по-прежнему является равномерно нагретым "газом частиц". В действительности спиральные рукава затрагивают и плоскую составляющую звездного фона. В численном, эксперименте дисперсия скоростей звезд в несколько раз больше, чем в реальных плоских звездных системах. Этот результат наглядно проявляется на рис. 38, где показаны круговая скорость вращения диска и угловые скорости газовой и звездной компонент. Видно, что угловая скорость центроида звезд в два раза меньше угловой скорости вращения диска, что и соответствует большой дисперсии скоростей звезд. Следует также отметить, что для появления спиральной структуры в описываемом численном: эксперименте была необходима некоторая начальная асимметрия диска. В реальных галактиках такая асимметрия могла быть связана с существованием баров.
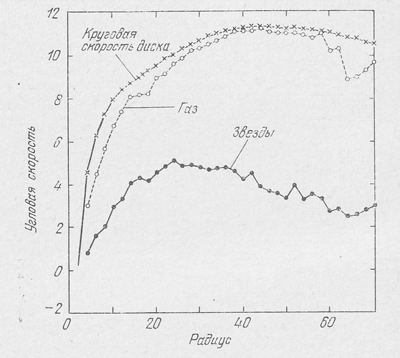
Рис. 38. Круговая скорость движения диска и угловые скорости его газовой и звездной компонент в численном эксперименте.
Дальнейшее развитие численного моделирования спиральной структуры проведено в работе Хокнея и Браунрига [42]. Во-первых, в ней было учтено влияние населения II типа. Для этого в выражение для потенциала (7.75) добавляется постоянный во времени потенциал, созданный сферическими подсистемами населения II типа. Далее расчет проводится тем же методом, причем рассчитаны модели с различным процентным составом населения II типа. Показано, что с увеличением доли этого населения стабилизация диска по отношению к распаду увеличивается, и если доля населения II типа составляет 80%, то диск оказывается устойчивым и образуются долгоживущие двухрукавные и многорукавные спирали. Во-вторых, в этой работе рассматривались и диски конечной толщины. Метод расчета в принципе прежний, только теперь пространство диска разбивалось на трехмерную сетку (число ячеек 32 × 32 × 16, рассматривалось движение 25000 звезд). Было показано, что трехмерный диск стабилизируется и спиральные рукава оказываются более устойчивыми. Авторы работы [42] нашли, что спиральные рукава в звездной системе образуются и без "охлаждения" системы - в противоположность результатам Миллера, Прендергаста и Квирка [36].
В работе Н. Н. Козлова, Р. А. Сюняева и Т. М. Энеева [39] образование спиральной структуры галактик связывалось с приливным действием одной галактики на другую. Правда, хотя спиральная структура, несомненно, является внутренним свойством, вращающегося диска галактики, возможно, что приливное действие со стороны других близких галактик может создавать свою спиральную структуру или как-то изменять вращение и форму диска. Численная модель приливного взаимодействия галактик, построенная в работе [39], заключается в следующем. Вокруг ядра галактики по круговым орбитам вращаются 800 в одних вариантах и 2000 в других вариантах не взаимодействующих между собой тел (спутников). Вращение происходит в одной плоскости и в одном направлении. Затем мимо этой системы на небольшом расстоянии пропускается второе тело с массой, равной массе ядра галактики. Рассмотрены разные варианты движения возмущенного тела - перпендикулярно и параллельно плоскости галактики, в прямом и обратном направлении по отношению к ее вращению. Прохождение возмущенного тела искажает круговые орбиты и приводит к появлению движения спиралеобразной формы. Результаты расчета представлены также в виде фильма, отдельные кадры из которого воспроизведены на рис. 39. Четко видна спиральная структура, сохраняющаяся в течение нескольких оборотов после прохождения возмущенного тела.
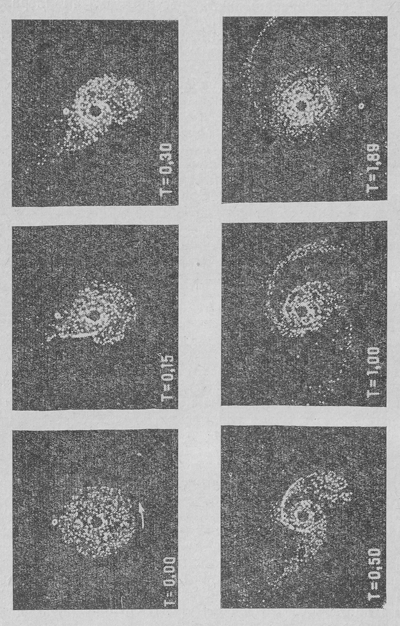
Рис. 39. Образование спиральных рукавово во вращающихся системах под влиянием приливного взаимодействия (кадры из фильма) .
Задача рассматривалась в трехмерном, пространстве, и было смоделировано искажение плоскости галактики под действием приливного взаимодействия. Как известно, плоскость диска межзвездной среды в нашей Галактике действительно искривлена и это явление часто приписывают приливному воздействию со стороны Магеллановых Облаков. В работе [39] получено также, что довольно много тел (до 12%) вырывается вообще из галактики при прохождении возмущенного тела. Тем самым численно промоделировано образование "мостов" между галактиками.
В работе [40] методом численного моделирования рассматривались уплощенные системы, где учитывалось и влияние толщины диска. Решалась система (7.1) но с потенциалом (7.62). Число звезд в разных вариантах - от 150 до 500. Основная цель численного эксперимента заключалась в изучении устойчивости и эволюции системы в зависимости от отношения кинетической энергии вращения к полной гравитационной энергии. Если задавать некоторую начальную конфигурацию трехмерной вращающейся звездной системы, то в процессе эволюции всегда увеличивается дисперсия скоростей и одновременно уменьшается средняя скорость вращения системы. Поэтому отношение средней кинетической энергии систематического движения звезд, т. е. кинетической энергии "чистого" вращения к гравитационной энергии должно все время уменьшаться. В работе [40] показано методом численного эксперимента, что это отношение стремится к 0,14 независимо от выбора ряда начальных условий.
В работе [40] отмечается также, что результат данного численного эксперимента (вообще говоря, согласующегося .и с другими численными экспериментами и показывающего, что во вращающейся звездной системе в квазиравновесном состоянии кинетическая энергия систематического движения звезд, т. е. вращения не больше 14% от полной гравитационной энергии) противоречит наблюдательным данным. В нашей Галактике орбиты звезд почти круговые, и кинетическая энергия движения звезд по аппроксимационным круговым орбитам, составляет существенно большую долю от гравитационной энергии. Расхождение может быть удастся устранить учетом роли сферических подсистем Галактики (гало Галактики)
Коллапс и бурная релаксация вращающихся звездных систем методом численного моделирования были исследованы в работе [41].
<< § 7.5 Численное моделирование эволюции звездных скоплений | Оглавление | § 8.1 Структура квазаров и ядер галактик >>