§ 4.5 Численное моделирование эволюции звезд
Объяснение эволюции звезд - одна из основных проблем астрофизики. Трудность решения этой проблемы заключается в том, что определение изменения во времени характеристик звезды по наблюдательным данным, как правило, оказывается почти невозможным. В этом случае численный эксперимент - единственная возможность получить ответ на многие вопросы.
Разные фазы состояния звезды имеют различные временные масштабы. На некоторых этапах (например, на главной последовательности) звезды задерживаются надолго, другие состояния (например, "провал" между главной последовательностью и ветвью гигантов) они "проскакивают" быстро. Но тем не менее, за исключением редких взрывных процессов, изменения состояния звезды в течение ее эволюции имеют более или менее квазистационарный характер. Это означает, что в каждый данный момент звезда находится в квазистационарном устойчивом состоянии, которое можно рассчитывать исходя из условий гидростатического равновесия и стационарного переноса энергии. Параметры же этого состояния относительно медленно меняются со временем.
Численный эксперимент в теории эволюции звезд заключается в том, что строится последовательность моделей звезд с меняющимися условиями и по последовательности моделей прослеживается звездная эволюция. Например, можно начать с однородной по химическому составу звезды, в лучистом равновесии, с конвективным ядром типа рассмотренных в предыдущем параграфе. В процессе сгорания водорода в конвективном ядре его концентрация уменьшается, но растет концентрация гелия. Легко подсчитать изменение X и Y за некоторый заданный промежуток времени Δt. Затем можно рассчитать модель с измененным неоднородным химическим составом и получить новые характеристики, изменившиеся за время Δt. Далее по новой модели рассчитывается изменение химического состава за следующий промежуток времени Δt, затем новая модель и т. д. Именно таким путам и строятся последовательности эволюционирующих звезд.
К настоящему времени рассчитано много эволюционных последовательностей звезд и сложилась определенная картина звездной эволюции, которую мы здесь и опишем. Более подробное изложение читатель найдет в книгах и обзорах [1, 8-11, 19-22].
Основные результаты расчета эволюции звезд обычно представляют в виде эволюционных треков - графиков, определяющих изменение светимости и поверхностной температуры (или радиуса) звезды заданной массы с течением времени. Часто эти треки имеют сложные петли, причем их форма может быть весьма разнообразной при очень небольшом различии исходных данных. Вероятно, эти петли, как и многие другие тонкие детали эволюционных треков, не отражают реальных изменений параметров звезд в процессе эволюции, но общее их направление, как можно надеяться, правильно передает характер эволюции звезд.
Сопоставление эволюционных треков, описывающих перемещение звезды по диаграмме Рессела-Герцшпрунга, с данными наблюдений затруднено тем, что мы не можем следить за эволюцией отдельных звезд. Кроме того, треки недостаточно наглядны, поскольку длины отдельных отрезков отражают особенности изменения параметров, а не длительность соответствующих этапов эволюции.
Поэтому наряду с эволюционными треками, которые можно было бы назвать "изомассами", на диаграмму Рессела-Герцшпрунга также наносят "изохроны" - линии положения точек, определяющих параметры звезд разной. массы, но прошедших эволюционный путь за одно и то же время. Такие изохроны можно сравнивать с наблюденными зависимостями между светимостью и эффективной температурой у отдельных скоплений, где, по-видимому, все звезды образовались одновременно и их возраст поэтому один и тот же. Помимо проверки правильности наших представлений об эволюции такие сравнения позволяют определить возраст скоплений.
Наконец, проверкой эволюционной теории является сопоставление с расчетами статистических зависимостей между светимостью, радиусом и массой звезд для определенных этапов их эволюции.
Теперь перейдем к качественному, но иллюстрируемому некоторыми графиками, описанию результатов численного моделирования эволюции звезд.
Эволюция звезд состоит из ряда отдельных этапов основными из которых являются протозвездная стадия, пребывание на главной последовательности, стадия красных гигантов, стадия сверхгигантов, взрывной этап эволюции, состояние белых карликов, нейтронных звезд и "черных дыр". Далеко не все эти стадии эволюции могут быть исследованы с одинаковой полнотой.
Легче всего поддаются расчету стадии эволюции, которые можно назвать квазистационарными. Здесь звезда в каждый момент времени находится в стационарном состоянии, и эволюция заключается в медленном переходе от одного стационарного состояния к другому близкому состоянию. Математически это предположение сводится к тому, что в уравнениях, описывающих структуру звезды, не выписываются члены, зависящие от времени, как это делалось в предыдущих параграфах этой главы. На нестационарных этапах эволюции приходится использовать уравнения с временными членами, и их интегрирование существенно усложняется. Таким образом, лучше всего изучены стадии пребывания на главной последовательности, стадии красных гигантов и белых карликов, т. е. такие этапы, на которых звезда задерживается подольше. Переходы между этими состояниями изучены хуже. Поскольку мы в первую очередь интересуемся результатами численного моделирования, то основное внимание будет уделено квазистацнонарным состояниям.
Протозвездная стадия существенно нестационарна, и поэтому пока не удалось построить набора достаточно полных моделей. Звезда начинает свою эволюцию со сжатия из-за гравитационной неустойчивости газо-пылевого облака, в котором благодаря сильному высвечиванию температура поддерживается на низком уровне (возможно, всего несколько градусов по шкале Кельвина). На самом первом этапе эволюции, когда протозвезда остается еще прозрачной для излучения, генерируемого внутри нее, она сжимается со временем свободного падения:
|
|
(4.84) |
Эта стадия существенно нестационарна и может рассчитываться лишь газодинамическими методами. Некоторые результаты здесь удалось получить с помощью метода автомодельных движений (см. гл. 6).
После того как звезда становится непрозрачной для излучения, начинается новая стадия. Поскольку выделение энергии еще велико, а большая величина коэффициента непрозрачности затрудняет лучистый перенос, то протозвезда переходит в состояние конвективного сжатия (стадия Хаяши). Процесс сжатия тоже быстрый, но медленнее, чем в состоянии свободного падения.
Сжатие происходит неоднородно - температура и плотность в центре протозвезды растут быстрее. В (результате здесь газ ионизуется, непрозрачность его уменьшается и в центре протозвезды образуется центральное лучистое ядро, масса которого все увеличивается. Чем больше масса протозвезды тем раньше образуется лучистое ядро, а у звезд с массами, меньшими 0,2 M☉, лучистые ядра вообще не образуются вплоть до перехода на главную последовательность. На стадии конвективного сжатия светимость протозвезды быстро уменьшается со временам, но через некоторое время после образования лучистого ядра светимость протозвезды выходит на некоторый постоянный уровень, соответствующий светимости звезды с данной массой (в соответствии с соотношением масса - светимость для звезд в лучистом равновесии).
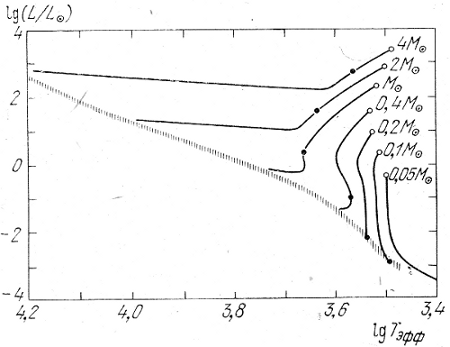
Рис. 4. Эволюционные треки протозвезд разных масс.
Заштрихована главная последовательность. Точки означают момент образования лучистого ядра (у более массивных протозвезд) или выход на главную последовательность (у менее массивных звезд).
Эволюционные треки протозвезд разных масс, начинающихся с одного и того же состояния средней плотности, приведены на рис. 4. Черной точкой обозначен момент образования лучистого ядра или выход на главную последовательность у звезд меньших масс. Протозвезды с массами, меньшими 0,05 M☉ вообще не выходят на главную последовательность, которая изображена на рис. 4 штриховой линией.
Изохроны протозвезд в состоянии конвективного сжатия изображены на рис. 5. Если нанести на зависимость "светимость - эффективная температура" положение протозвезд разной массы, начинающих свое сжатие в один и тот же момент времени с состояния одинаковой плотности, то получатся линии, изображенные на рис. 5 для времен существования протозвезд (сверху вниз): 104 лет, 105 лет, 106 лет, 107 лет и 108 лет. Естественно, что чем больше масса протозвезды, тем быстрее она сжимается до состояния главной последовательности. Процесс сжатия может несколько замедлиться при сгорании легких элементов типа лития, бериллия и бора, но поскольку они не возобновляются
в термоядерных реакциях в звездах, то этот этап существенного значения для эволюции звезды не имеет.
Переход на главную последовательность соответствует включению основных термоядерных источников энергии - горению водорода в центральной части звезды. Быстрый рост выхода энергии после включения термоядерных источников приводит к образованию конвективного ядра в центре звезд с массой, большей массы Солнца. В центрах звезд меньших масс остается лучистое ядро, а конвекция сохраняется только во внешних слоях, а у звезд с массами, меньшими 0,25 ☉, конвекция по-прежнему сохраняется по всей звезде. Звезды с очень малыми массами переходят в состояние вырожденных звезд, так и не достигнув температуры, необходимой для включения термоядерных реакций.
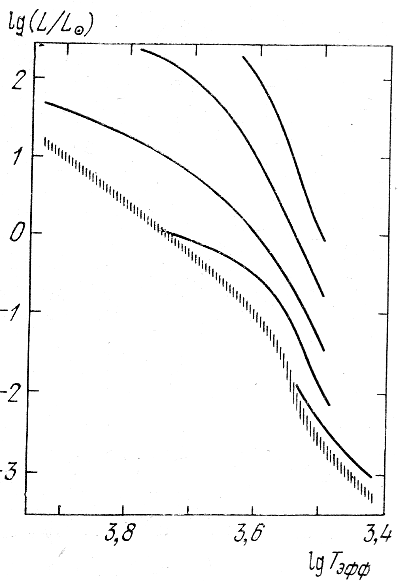
Рис. 5. Изохроны сжимающихся протозвезд.
Заштрихована главная последовательность. Линии соответствуют следующим возрастам протозвезд (сверху вниз): 104, 105, 106, 107 и 108 лет.
Эволюция звезд зависит и от начального химического состава. Грубо можно разделить все звезды на два поколения. Звезды первого поколения начали свою эволюцию на начальных этапах развития галактик, когда в первичном веществе почти не было тяжелых элементов. Здесь величина Z - содержание всех элементов, кроме водорода и гелия, по числу атомов - мала, вероятно, порядка 10-4 или меньше. Сейчас эти звезды составляют население эллиптических галактик и сферических подсистем нашей Галактики (звездное население II типа). Звезды второго поколения образовались из межзвездного вещества, обогащенного тяжелыми элементами в процессе эволюции. Здесь Z ≈ 0,02-0,04. Они составляют основное звездное население плоских подсистем спиральных и иррегулярных галактик (звездное население I типа).
Структура звезд первого и второго поколений во время их пребывания на стадии горения водорода в общем более или менее одинакова (для звезд одинаковых масс), но светимости различаются. Звезды первого поколения имеют меньшую светимость и принадлежат не главной последовательности, а параллельной ей последовательности субкарликов. Конвективные ядра у звезд первого поколения меньше. Правда, массивных звезд первого поколения уже не осталось, а менее массивные звезды конвективных ядер не имеют.
Более подробно изучена эволюция звезд второго поколения и ниже мы приведем численные данные для этих звезд. У менее массивных звезд, температура в центре которых меньше 1,8 ⋅ 106 градусов, основным источником энергии является протонный цикл, описываемый формулой (4.26). У более массивных звезд с более высокой внутренней температурой основным источником термоядерной энергии является углеродно-азотный цикл (формула (4.27)). Резкая зависимость выхода энергии от температуры в последнем случае и определяет образование конвективных ядер у массивных звезд. Можно считать, что звезды с углеродно-азотным циклом имеют конвективные ядра, а звезды с протонным циклом - конвективные поверхностные зоны. У звезд первого поколения роль углеродно-азотного цикла существенно меньше и поэтому у них заметно меньше и конвективные ядра.
В процессе пребывания на главной последовательности происходит превращение водорода в гелий в центральном ядре звезды. Рассмотрим сначала массивные звезды с конвективными ядрами. Здесь из-за конвекции происходит перемещение вещества и поэтому содержание водорода уменьшается одновременно во всем конвективном ядре. Для того чтобы сохранить мощность излучения на уровне, требуемом соотношением масса - светимость, температура и плотность в центре звезды несколько повышаются (температура - па 10-15%, плотность - на 15-20%). Одновременно происходит и уменьшение самого конвективного ядра как по размерам, так и по массе. При уменьшении начального содержания водорода от 60-70% до 3-5% масса конвективного ядра уменьшается в 2-3 раза. Радиус и светимость звезды растут, и она передвигается по диаграмме Рессела - Герцшпрунга вверх и влево, но оставаясь в пределах главной последовательности. Поэтому можно считать, что ниже ля кромка главной последовательности есть положение звезд, только что попавших на эту последовательность.
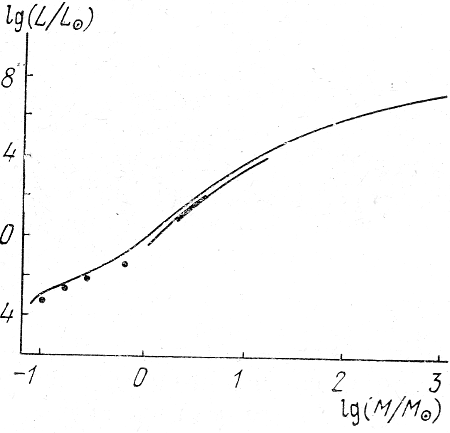
Рис. 6. Расчетная зависимость масса-светимость главной последовательности.
Верхняя кривая соответствует звездному населению I типа, нижняя кривая и точки - II типу.
У меньших по массе звезд перемешивания нет и поэтому в процессе сгорания водорода в центре образуется небольшое ядро, в котором постепенно растет отношение гелия к водороду. Уменьшающееся содержание водорода при сохранении полной мощности излучения также требует некоторого повышения температуры и плотности, а следовательно, и сжатия центрального гелиевого ядра. И здесь звезда остается на главной последовательности, перемещаясь вверх и влево. У малых по массе звезд в процессе выгорания водорода в центре возникает вырождение электронного газа из-за сильного увеличения плотности.
У звезды данной массы ее светимость и радиус мало меняются и за время пребывания на главной последовательности. Поэтому можно использовать соотношения масса - светимость и масса - радиус, полученные выше из соображений размерности и подобия. Численные расчеты моделей звезд разных масс позволили построить более точные теоретические зависимости, которые мы приведем в графическом виде (рис. 6-12, заимствованные из работы Г. Рубена [21]).
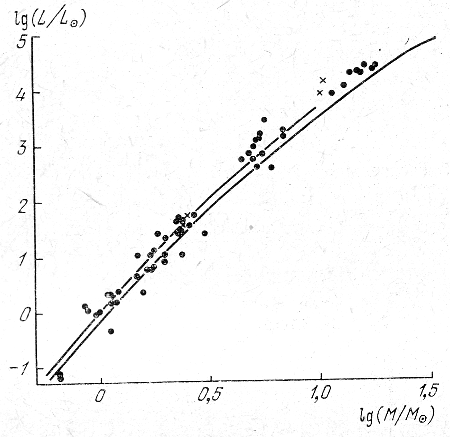
Рис. 7. Сопоставление теоретических расчетов соотношения масса - светимость с наблюдательными данными.
Расчетная зависимость масса - светимость приведена на рис. 6. Верхняя кривая соответствует звездному населению I типа (с большим содержанием тяжелых элементов), нижняя кривая и точки - населению II типа. Сопоставление с данными наблюдений дано на рис. 7, где нанесены точки, соответствующие определениям масс разных звезд. Разброс наблюдательных данных относительно небольшой и, вероятно, в значительной мере определяется неточностью определения масс из наблюдений.
Из рис. 6 сразу видно, что зависимость масса - светимость нельзя представить одной степенной кривой вида
|
|
(4.85) |
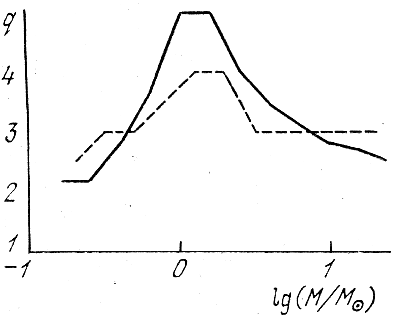
Рис. 9. Значение показателя (формула (4.85)).
Сплошная кривая - расчетные данные пунктир - аппроксимация наблюдений.
Это очевидно следует и из выражений (4.67), (4.69) - (4.71). В самом деле, по мере перехода от одних масс к другим меняется коэффициент непрозрачности, а также показатель степени в температурной зависимости закона выделения энергии. Поэтому показатель q должен меняться. На рис. 8 приведено изменение показателя q в зависимости от массы, определенное как на основании расчетов моделей (сплошная линия), так и по аппроксимации наблюдательных данных (пунктирная линия). Расчеты показывают несколько больший интервал изменений показателя q, чем наблюдения. В области масс, сравнимых с массой Солнца, из формулы (4.69) следует q = 191/37 = 5,2; более точные расчеты моделей дают q ≈ 4,75, а из данных наблюдений получается q ≈ 4. В области больших масс формула (4.71), теоретические расчеты и наблюдения приводят к близким значениям q ≈ 3. С другой стороны, в области малых масс, где велика роль конвекции, показатель q существенно уменьшается. Это также согласуется с теоретическими оценками на основе размерностных соображений, приведенных в 4.2.
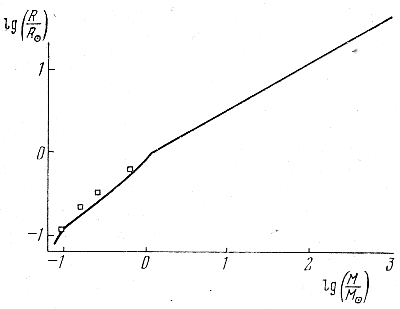
Рис. 9. Расчетная зависимость радиуса звезд главной последовательности от массы.
На рис. 9 приведена расчетная зависимость масса - радиус для звезд главной последовательности. Перелом линии в области массы Солнца связан с исчезновением конвективной поверхностной зоны у звезд больших масс. Для этого интервала масс зависимость радиуса от массы приближенно описывается соотношением R ∼ M0,5. Из формулы (4.67) следует более сильная зависимость R ∼ M0,7. Наблюдательные данные (рис. 10) подтверждают теоретическую зависимость. Таким образом, зависимость масса - радиус оказалась более чувствительной к точности расчета.
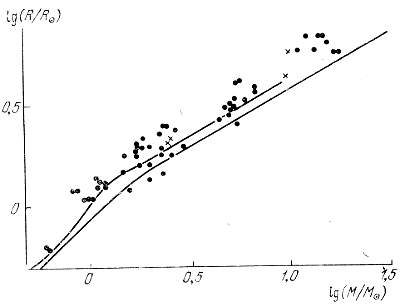
Рис. 10. Сопоставление теоретической зависимости радиус - масса с данными наблюдении.
Зная соотношения масса - светимость и масса - радиус, можно построить и основную зависимость для главной последовательности - диаграмму Рессела - Герцшпрунга, т. е. зависимость светимость - эффективная температура Tэфф, что эквивалентно зависимости светимость - радиус, поскольку Tэфф = L/4πσR2. Расчетные кривые для зависимости светимость - эффективная температура, построенные разными авторами (римские цифры), приведены на рис. 11. Жирная линия и отдельные точки в области низких светимостей соответствуют наблюдательным данным. Как видно, согласие теории и наблюдений здесь очень хорошее.
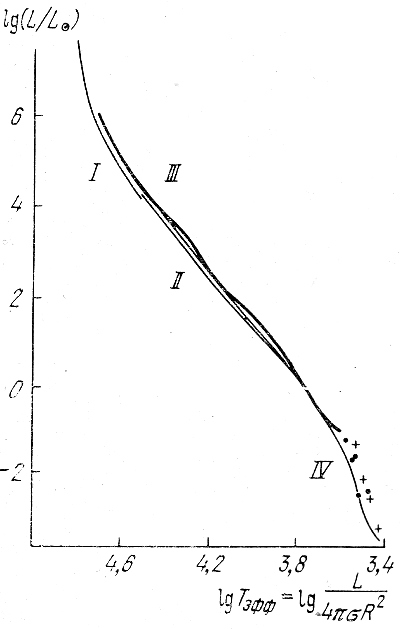
Рис. 11. Диаграмма Рессела-Герцшпрунга, эквивалентная зависимости радиус-светимость для звезд главной последовательности.
Тонкие линии, обозначенные римскими цифрами, - результаты различных расчетов, жирная линия - средняя кривая по данным наблюдений. В области низких светимостей наблюдений мало, нанесены отдельные точки.
Таким образом, можно утверждать, что теоретические расчеты звездных моделей главной последовательности оказались в хорошем согласии с данными наблюдений. Основные характеристики этих моделей могут быть с более или менее удовлетворительной точностью описаны и на основе соображений анализа размерностей, хотя в некоторых случаях наблюдаются расхождения между расчетными моделями и соотношениями, полученными из условий подобия. Здесь всегда надо иметь в виду, что, строго говоря, каждой массе звезды соответствует своя модель. Подобие касается только общих характеристик моделей.
Звезда остается на главной последовательности до тех пор, пока содержание водорода в ее центральной части не уменьшится до нескольких процентов, с чем связано образование в ее центре гелиевого ядра. Масса гелиевого ядра не может быть велика, она не больше 10% от массы звезды и у массивных звезд не превышает 0,4-0,6 M☉. После того как содержание водорода окажется меньше 1%, начнется сжатие гелиевого ядра, звезда сойдет с главной последовательности и перейдет к области красных гигантов. Прежде чем обсуждать расчеты продвинутых стадий эволюции звезд, приведем таблицу характерных времен (в годах) пребывания звезд разных масс и различного химического состава на стадии главной последовательности (табл. 5) [20, 21, 23, 24].
| Масса, M/M☉ | Начальный состав: X=0,7, Y=0,02 |
Увеличенное содержание водорода: X=0,9, Y=0,01 |
Почти полное отсутствие тяжелых элементов: Z=0 ÷ 0,0001 |
| 100 | — | — | 3,6 ⋅ 106 |
| 64 | 2,5 ⋅ 106 | — | — |
| 32 | 4 ⋅ 106 | — | 6,6 ⋅ 106 |
| 16 | 8 ⋅ 106 | 1,5 ⋅ 107 | 107 |
| 10 | 2 ⋅ 107 | — | 2,5 ⋅ 107 |
| 6 | 7 ⋅ 107 | 1,2 ⋅ 108 | 1,1 ⋅ 108 |
| 3 | 2 ⋅ 108 | — | — |
| 2,25 | 5 ⋅ 108 | — | — |
| 1,5 | 1,5 ⋅ 109 | — | — |
| 1,2 | 2,9 ⋅ 109 | 1010 | — |
| 1,0 | 7 ⋅ 109 | 2 ⋅ 1010 | — |
Приведем еще одну полезную таблицу (см. [20]), в которой даны значения светимости массы звезды в зависимости от ее возраста в тот момент времени, когда звезда покидает главную последовательность (табл. 6).
Как и следовало ожидать, с увеличением массы время пребывания звезды па главной последовательности
| Возраст в годах | lg(L/L☉) | lg(M/M☉) | ||
| X=0,65 | X=0,90 | X=0,65 | X=0,90 | |
| 8 ⋅ 109 | 0,60 | 0,73 | 0,82 | 1,27 |
| 10 ⋅ 109 | 0,51 | 0,63 | 0,78 | 1,19 |
| 12 ⋅ 109 | 0,43 | 0,55 | 0,75 | 1,14 |
| 16 ⋅ 109 | 0,31 | 0,42 | 0,70 | 1,06 |
| 20 ⋅ 109 | 0,22 | 0,33 | 0,66 | 1,00 |
быстро уменьшается, примерно как M/L ∼ M1-q. Увеличение содержания водорода и уменьшение содержания тяжелых элементов несколько увеличивает время эволюции, но не очень существенно.
Табл. 6, в которой даны светимости и массы звезд в момент их схода с главной последовательности, очень удобна для определения возраста галактических скоплений звезд, у которых удается точно определить положение главной последовательности для наиболее ярких звезд.
После образования в центре звезды гелиевого ядра достаточного размера (по-видимому, около 10-15% от массы всей звезды, так называемый предел Шенберга - Чандрасекара) термоядерные источники уже не в состоянии поддерживать температуру и давление на необходимом уровне. Центральная часть звезды начинает сжиматься, и некоторое время звезда живет за счет гравитационных источников энергии. В окружающем гелиевое ядро слое повышается температура и там загорается водород. Появляется звезда со слоевым источником энергии. Сначала в слоевом источнике находится несколько процентов массы звезды, но затем его толщина уменьшается и масса слоя термоядерных реакций составляет всего 0,5% от массы звезды.
Образование слоевого источника и неустойчивость звезд с большими гелиевыми ядрами приводит к резкому изменению внешних параметров звезды: светимости, радиуса, поверхностной температуры. В самом деле, из-за неустойчивости гелиевого ядра оно начинает быстро сжиматься, что сопровождается повышением температуры как в самом ядре, так и в слоевом источнике. Это и приводит к уменьшению толщины слоевого источника. В результате градиент температуры внутри звезды оказывается резко различным. Гелиевое ядро изометрично, а в слоевом источнике температура резко падает на очень небольшой толщине.
Большая величина градиента возможна только в слоях с хорошей прозрачностью. Поэтому прилегающие к источнику слои расширяются, а с ними расширяется и поверхность звезды. Радиусы звезд со слоевыми источниками, как правило, велики. Светимость таких звезд тоже меняется, но не так сильно, и поэтому поверхностная температура падает. Иными словами, звезды со слоевыми источниками горения водорода оказываются на последовательности красных гигантов.
Звезды проходят последовательность слоевых источников два, а возможно, и три раза - стадии горения водорода, гелия, углерода. В промежутке между стадиями слоевых источников имеются этапы горения соответствующих элементов в ядрах звезд. Каждый раз на стадии слоевого источника звезда расширяется, а на этапе горения в ядре - сжимается. В результате звезда проходит на диаграмме Рессела - Герцшпрунга довольно сложный эволюционный трек, схематически изображенный на рис. 12. Здесь буквами обозначены различные этапы эволюции, описание которых дано ниже. У звезд разных масс характер эволюции несколько отличается, но общая последовательность ее этапов одна и та же.
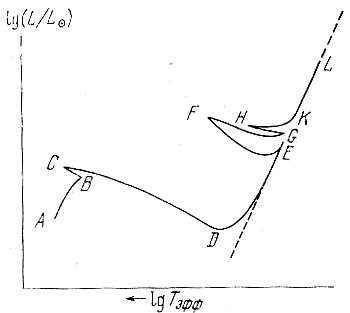
Рис. 12. Схематическое изображение эволюционного трека звезды после ухода ее с главной последовательности.
Буквами обозначены отдельные этапы, описание которых дано в тексте. Пунктирная линия справа - граница Хаяши, соответствующая конвективному переносу энергии по всей звезде.
Изменение строения звезды в процессе ее эволюции удобно характеризовать схемой, изображенной на рис. 13 и 14 (заимствованы из статей Киппенхана и его сотрудников в сборниках [10] и [11]). Здесь указаны заштрихованные области термоядерных источников (прямая штриховка) и конвективного переноса энергии (круглая штриховка). Для удобства построения графиков использованы разные шкалы времени. Эта схема рассчитана для звезд с массой 7 М☉; для других масс звезд картина примерно такая же, но масштабы шкал меняются. На основании рис. 12-14 легко дать качественное описание всей эволюции звезды.
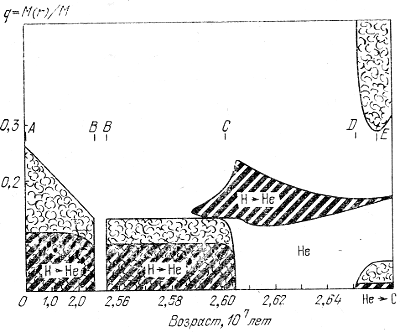
Рис. 13. Схематическое изменение строения звезды в процессе ее эволюции на этапе горения водорода.
Изображены этапы А-Е. Круглой штриховкой отмечены конвективные области, жирной штриховкой - области термоядерных реакций (с указанием типа превращений элементов). Шкала времени меняет масштаб на разрыве графика
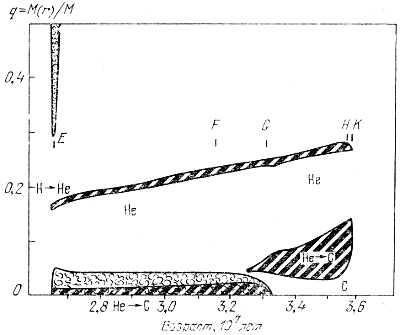
Рис. 14. Продолжение рис. 13 - стадия горения гелия. Изображены этапы Е - К. Шкала времени опять изменена.
Этап А - В соответствует пребыванию звезды на главной последовательности. Следует обратить внимание на уже отмеченное уменьшение массы конвективного ядра. В точке В изменен масштаб шкалы времени. На этапе В - С происходит сжатие центрального ядра на стадии исчерпания последних остатков водорода и появление слоистого источника. Видно, что часть массы, занимаемая слоистым источником, сначала велика, но быстро уменьшается. Этап С - D соответствует быстрому увеличению размеров звезды и переходу к стадии красных гигантов. У звезд больших масс этот переход происходит быстро и звезда как бы "проскакивает" область между главной последовательностью и красными гигантами. У звезд (меньших масс (примерно при М < 1,5 М☉) переход происходит медленнее и наблюдается непрерывная полоса, соединяющая главную последовательность с красными гигантами. Это, в частности, связано с тем, что масса гелиевого ядра меньше, поскольку нет перемешивания, поэтому неустойчивость не развивается. Кроме того, у таких звезд переход к состоянию слоевого источника связан с заметным увеличением светимости (больше толщина этого слоя) и поэтому, если звезды больших масс, сходя с главной последовательности, движутся по диаграмме Рессела-Герцшпрунга преимущественно горизонтально (на этом этапе см. рис. 12), то звезды меньших масс проходят этот этап ближе к вертикали. Это связано с большей ролью конвективного переноса энергии у таких звезд. Впрочем, поверхностные конвективные зоны на этапе красных гигантов развиваются и у более массивных звезд (см. этап D - Е на рис. 13). И здесь в области развития конвекции звезда идет вверх на диаграмме Рессела - Герцшпрунга (см. рис. 12), так как конвекция может переносить существенно больший поток энергии, т. е. привести к увеличению светимости.
В фазе горения водорода в слоистом источнике сжатие гелиевого ядра продолжается, хотя происходит медленнее. Температура повышается, и когда она достигнет примерно 108 градусов, в гелиевом ядре включается реакция тройного соединения ядер гелия в одно ядро углерода С12 (см. формулу (4.28)). Здесь выход энергии очень сильно зависит от температуры, и поэтому включение этой реакции опять приведет к возникновению конвективного ядра в центре звезды (этап Е - F на рис. 12 и 14). Звезда сжимается, относительные градиенты температуры тоже уменьшаются, т. е. звезда становится более однородной по своему строению и в какой-то мере напоминает состояние звезды на главной последовательности. Правда, она стала существенно более яркой. Кроме того, продолжает действовать слоистый водородный источник на некоторой, все увеличивающейся, высоте над центральным ядром, где горит гелий. Этот слоистый источник дает заметный вклад в общую светимость звезды.
Запасов гелия в ядре достаточно, и поэтому характерное время существования звезды в стадии горения гелия в ядре всего лишь в десять раз меньше, чем на стадии горения водорода (это связано с увеличенной светимостью). Стадию горения гелия в ядре проходят звезды всех масс, больших примерно 0,5 M☉. У меньших по массе звезд при образовании гелиевого ядра возникает электронное вырождение, и при сжатии ядра в дальнейшем температура уже не растет - поэтому не достигается состояние, при котором загорается гелий. У звезд несколько больших масс (но меньших 3 М☉) возможно появление так называемой "гелиевой вспышки". Суть этого явления заключается в следующем.
Если в гелиевом ядре, состоящем из обычного невырожденного газа, температура повышается настолько, что загорается гелий, то при этом выделяется большое количество энергии, увеличивающей температуру и давление. Ядро начинает расширяться, что замедляет или даже останавливает быстрый рост температуры. В результате включение гелиевой реакции происходит медленно и плавно. В гелиевом ядре, состоящем из частично вырожденного электронного газа, картина иная. Выделение энергии повышает температуру, но давление растет медленнее, поскольку оно теперь связано с вырождением электронного газа. Рост температуры продолжается, что еще больше увеличивает выход энергии - происходит своеобразный взрыв, и только последующее расширение при более высоких температурах снимает вырождение электронного газа. Пока не ясно, какую роль в эволюции звезды могут играть подобные гелиевые вспышки. У массивных звезд (эволюция которых, например, изображена на рис. 12-14) вырождения в центральных частях нет и поэтому не могут возникать гелиевые вспышки.
На этапе F - G постепенно уменьшается содержание гелия в ядре звезды и образуется углеродное ядро. Горение гелия затухает, когда его остается меньше 30%. Здесь опять повторяется картина эволюции. Центральное изотермическое ядро сжимается, а гелий загорается в слоистом источнике. Возникает новая стадия звезды со слоистым источником. Точнее здесь уже два слоистых источника, ибо горение водорода в относительно более высоких слоях звезды продолжается. Звезда переходит в область сверхгигантов (этапы G - H - К на рис. 12, 14). Эти этапы эволюции звезд рассчитываются с очень большой неуверенностью - состояние звезды быстро меняется и трудно оценить вклад различных механизмов выделения и переноса энергии. В табл. 7 приведены полные суммарные характерные времена (в годах) пребывания звезд на стадии красных гигантов и перехода к этой стадии (т. е. образования и горения водорода в слоистом источнике), полученные на основании усреднения результатов ряда расчетов (см. [20, 23]).
| Масса звезды в массах Солнца | Звезды нормального состава (население I) | Звезды первого поколения (население II) |
| 64 | 5 ⋅ 103 | — |
| 32 | 1,5 ⋅ 104 | — |
| 25 | 1,3 ⋅ 106 | — |
| 15 | 2 ⋅ 106 | — |
| 10 | 4 ⋅ 106 | — |
| 5 | 2 ⋅ 107 | — |
| 3 | 7 ⋅ 107 | — |
| 1,5 | 4 ⋅ 108 | 1010 |
| 1,0 | 4 ⋅ 109 | 2 ⋅ 1010 |
Впрочем, надо отметить, что данные расчетов разных авторов заметно расходятся. Расчеты эволюции звезд представляют особый интерес в связи с проблемой нуклеосинтеза - образования различных элементов в звездах. Здесь как раз наиболее интересны последние этапы эволюции звезд - загорание углерода в ядре, построение более тяжелых элементов путем захвата нейтронов и т. п. Но в данной книге мы обсуждаем только вопросы моделирования строения звезд и поэтому не будем излагать эти очень важные проблемы.
Рассмотрим теперь расчет эволюции тесных двойных систем. При расчете эволюции одиночных звезд обычно считается, что масса звезды в процессе эволюции не меняется. Однако если эволюционирующая звезда входит в состав тесной двойной системы и если она в процессе изменения параметров расширяется настолько, что заполняет свою полость Роша, то такая звезда может интенсивно терять массу, и это нужно учитывать при расчетах.
Как известно, полость Роша ограничена такой поверхностью, что при пересечении ее частица, летящая от звезды, сможет далее беспрепятственно от нее удалиться. Полости Роша двух звезд соприкасаются в "так называемой критической точке Лагранжа, лежащей на линии, соединяющей центры этих звезд. Формулы, определяющие уравнение поверхности Роша, довольно сложны, но если отношение масс звезд находится в определенных пределах, то в первом приближении (правда, довольно грубом) их можно считать сферами с радиусами, для нахождения которых можно воспользоваться аппроксимационной формулой:
|
|
(4.86) |
Здесь M1 и M2 - массы звезд (в дальнейшем индексом 1 будем обозначать главную звезду с большей массой), r1 - радиус полости Роша вокруг первой звезды, а - расстояние между звездами пары.
Если одна звезда заполняет свою полость Роша, а другая нет, то такие системы называют полуразделенными, если же обе звезды заполняют свои полости Роша, то система является контактной.
Эволюция двойной системы рассматривается в трех предположениях о порядке заполнения полости Роша (см., например, [25]). В случае А полость Роша заполняется еще на стадии главной последовательности - это может произойти в системах, у которых расстояние между компонентами порядка или меньше (5 - 20) R☉, где R☉ - радиус Солнца. После потери значительной части массы первичная компонента опять уменьшается в размерах, и истечение вещества ослабляется. Поэтому эта стадия эволюции ограничена во времени. Любопытно, что можно получить характеристики этого этапа эволюции из очень простых качественных соображений. Дело в том, что истечение вещества определяется не столько эволюцией ее основной части, сколько самим фактом заполнения полости Роша. Поэтому характерное время истечения вещества, заполнившего полость Роша, по порядку величины есть время заметного выделения гравитационной энергии в среде с радиусом, равным размеру полости Роша r1 и со светимостью порядка светимости самой звезды на этом этапе эволюции LA, т. е.
|
|
(4.87) |
Скорость потери массы (считая, что она заметна)
|
|
(4.88) |
В конкретных расчетах получаются более точные значения, но эти формулы могут быть использованы для оценок по порядку величины.
Истечение массы из главной компоненты (при M1 > M2) и выпадение ее на вторую компоненту в конечном счете обращает это отношение, так что окажется M2 > M1, и вторичная компонента станет эволюционировать быстрее.
Но и в первичной компоненте продолжается горение водорода и поэтому ее светимость окажется большей, чем светимость нормальной звезды той же (т. е. уменьшенной) массы. Первичная звезда оказывается субгигантом со светимостью примерно на 3m большей нормальной звезды. Надо, однако, заметить, что на продвинутой стадии эволюции пары в случае А порядки отношений масс M1/M2 и светимостей L1/L2 обеих компонент не слишком сильно отличаются от единицы. Типичным примером таких звезд является звезда типа β Лиры.
Во втором случае (называемом случаем В) заполнение полости Роша возникает тогда, когда звезда расширяется на стадии сжатия изотермического гелиевого ядра и появления слоевого водородного источника. Здесь расстояние между компонентами может быть много больше - от 30 до 200R☉. Заметим, что в результате потери массы из системы в случае A расстояние между компонентами увеличивается и поэтому случаи A и В могут произойти с одной и той же парой.
И в случае В истечение вещества из звезды-гиганта, заполнившего свою полость Роша, относительно слабо зависит от того, что делается в ее центральной части. Поэтому и здесь могут быть использованы оценки (4.88) и (4.89) для определения характерных времен и скоростей потери массы, если оболочка находится в лучистом равновесии. Правда, если оболочка звезды, заполнившей полость Роша, оказалась в состоянии конвективного переноса энергии и вообще имеет неустойчивый характер, то время заметной потери массы сравнимо со временем спадания, т. е. с величиной порядка ![]() . Тогда потеря массы резко возрастает.
. Тогда потеря массы резко возрастает.
Расширение оболочки звезды и заполнение ею полости Роша продолжается на стадии слоевого источника до тех пор, пока это расширение не останавливается загоранием гелия в ядре. Следовательно, эволюция тесных двойных систем в случае В определяется характером загорания гелия, а это в свою очередь зависит ст массы. При относительно больших массах (например, при M > 3 M☉) загорание гелия происходит беспрепятственно, гелиевое ядро опять расширяется и оболочка звезды отделяется от полости Роша. Здесь стадия истечения непродолжительна. При меньших массах главной компоненты на стадии слоевого источника в изотермическом ядре появляется частичное выражение, и поэтому загорание гелия не сопровождается резким расширением ядра и соответствующим сжатием оболочки. Фаза истечения вещества в случае В продолжительнее и поэтому звезда теряет большую массу. По окончании этой фазы отношение масс компонент может упасть до 1/5 или даже 1/10. Светимость главной компоненты может на три-четыре порядка превышать светимость обычных звезд таких масс. К этому классу звезд относятся звезды типа Алголя.
Рассматриваемая фаза эволюции заканчивается тогда, когда почти весь водород в бывшей главной компоненте выгорел и сильно уменьшенный по массе остаток ее оказался гелиевым или частично углеродным белым карликом.
У очень массивных звезд (M > 15 M☉) полость Роша может заполняться еще раз во время фазы слоевого гелиевого источника и сжатия углеродного ядра (случай C). Качественная картина здесь аналогична, но детальных расчетов почти нет.
В качестве примера расчета эволюции тесных двойных звезд приведем результаты А. В. Тутукова, Л. Д. Юнгельсона, А. Я. Клеймана [26], рассматривавших тесные пары с отношением масс M1/M2 = 1,07 при массах первичной компоненты в начале эволюции 10 M☉ ≤ M1 ≤ 64 M☉.
В случае А, т.е. при а ≈ (20 - 30) R☉, через 106 лет после начала эволюции заполняется полость Роша и примерно за 104 лет теряются первые 15-25% начальной мдссы главной компоненты. Затем происходит спад поверхности к состоянию равновесной модели с уменьшенной массой, затем вновь расширение и опять истечение, но более медленное - еще 25-35% от начальной массы за (2-3) ⋅ 106 лет. В конце эволюции в случае А отношение масс M1/M2 ≈ 0,33-0,4. Для больших расстояний между компонентами, т. е. в случае В при а ≈ (70 - 170) R☉, полость Роша заполняется при слоевом водородном источнике. Здесь также обнаружены две фазы истечения вещества. В первой, быстрой фазе теряется за 103 лет около 50-70% начальной массы главной компоненты и в течение второй, медленной фазы за время порядка 105 лет теряется не более одной массы Солнца. Полная длительность эволюции с исчерпанием в случае В примерно в 10 раз меньше характерного времени пребывания на главной последовательности.
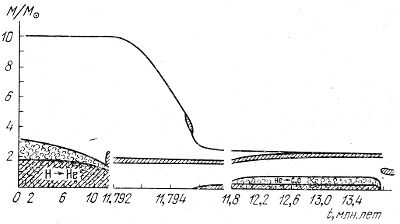
Рис. 15. Изменение массы и структуры звезды с начальной массой 10 М☉, входящей в тесную двойную систему.
Истечение на стадии красного гиганта (случай В). Обозначения те же, что на
рис. 13, 14.
На рис. 15 приведена схема изменения структуры звезды, из которой на стадии В происходит истечение вещества (на рисунке дважды меняется шкала времени). Рассмотрен случай звезды с массой 10 М☉. На главной последовательности масса не меняется, сжатие ядра после исчерпания водорода приводит к быстрой потере массы, продолжающейся до загорания гелия, когда звезда опять сжимается. Структура звезды в тесной паре по характеру такая же, как и в случае одиночной звезды, но слоистый водородный источник оказывается гораздо ближе к поверхности звезды и в конечном счете выходит почти на саму поверхность. На стадии горения углерода происходит еще одно заполнение полости Роша (случай C). Эта фаза истечения непродолжительна, порядка 03 лет, и теряется всего примерно 0,2 M☉.
Для оценки роли эволюции в тесных двойных системах особое значение имеет определение массы остатка звезды после истечения из нее вещества. Численные расчеты дают следующую аппроксимационную формулу для массы остатка Mf:
|
|
(4.89) |
где, напоминаем, M1 - начальная масса главной компоненты. Согласно этой формуле в белые карлики (Mf ≤ 1,44 M☉) превращаются звезды с M1 ≤ 6 M☉, в нейтронные звезды (Mf ![]() 10 M☉) превращаются звезды с 714^10 Ме,а более массивные звезды должны превращаться в "черные дыры".
10 M☉) превращаются звезды с 714^10 Ме,а более массивные звезды должны превращаться в "черные дыры".
К сожалению, сам процесс превращения звезды в белый карлик, нейтронную звезду или "черную дыру" не удается рассмотреть сколько-нибудь надежным способом. Отчасти это объясняется тем, что такой процесс существенно нестационарен, трудно составить необходимую систему уравнений и тем более трудно ее решать. Даже методы анализа размерностей и подобия пока не смогли дать здесь какую-либо информацию. В заключение настоящего параграфа приведем любопытный график, построенный В. Ю. Теребижем. Как уже отмечалось, в стационарном состоянии светимость звезды не может превысить эддингтоновский предел (см. (3.34)). Поэтому можно ожидать, что в тех случаях, когда эволюция звезды проходит через последовательность квазистационарных состояний, ее меняющаяся светимость не может перейти через предел Эддингтона. На рис. 16 еще раз приведена зависимость масса - светимость для разных типов звезд (а не только для главной последовательности, как в случае рис. 7). Здесь нанесены также звезды типа Вольфа - Райе, типа Be, белые карлики.
Однако для сопоставления с теорией теперь необходимо более точно определить эддингтоновский предел светимости. Такой расчет и был проведен В. Ю. Теребижем для ряда предположений. Запишем выражение для предела светимости в виде
|
|
(4.90) |
Отличие от (3.34) заключается в следующем. Во-первых, здесь учтено влияние центробежной силы (vR - линейная скорость вращения на экваторе). Во-вторых, учитывается возможная роль других механизмов поглощения излучения. Это сделано введением двух множителей А и I. Величина
|
|
(4.91) |
где Ai - атомный вес i-го элемента и zi - его обилие, учитывает полный вес всех элементов в единице объема. Параметр
|
|
(4.92) |
учитывает давление излучения при поглощении света различными атомами и ионами. Здесь n - полная концентрация частиц, ne - концентрация электронов, nij - концентрация атомов и ионов i-го сорта в j-м состоянии ионизации. Под kij(ν) следует понимать коэффициенты поглощения и рассеяния во всех линиях и за границами серий. При расчете для функции L(ν) принято планжовское распределение с температурой, соответствующей эффективной температуре звезд. Минимум на кривых 1 и 2 обусловлен вкладом ионизованного гелия. В атмосфере, состоящей только из полностью ионизованного водорода, A = 1 и I = 1.
На рис. 16 линия E означает обычный эддингтоновский предел светимости при vR = 0, A = 1, I = 1. Линия R соответствует учету вращения. Здесь принято vR = 436 км/сек, A=1, I=1. Кривые 1 и 2 соответствуют учету множителя A/I. Они рассчитаны для смеси водорода и гелия в предположении, что средняя концентрация частиц в слоях с оптической глубиной в резонансных линиях n ≈ 3 ⋅ 1011 см-3 (кривая 1) или n ≈ 3 ⋅ 1012 см-3 (кривая 2).
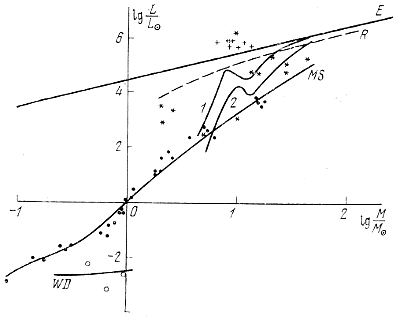
Рис. 16. Пределы светимости звезд.
Е - эддингтоновский предел светимости невращающихся звезд; R - предел светимости при учете вращения (vR = 436 км/сек); I - поглощение смесью водорода и гелия при n ≈ 3 ⋅ 1011 см-3; 2 - то же, но при n ≈ 3 ⋅ 1012 см-3; MS - главная последовательность; WD - белые карлики. Обозначения звезд: &hellip - главная последовательность; °;°;°; - белые карлики; +++ - звезды типа Вольфа - Райе; * * * - звезды типа Be.
График рис. 16 показывает, что быстро вращающиеся звезды типа Be действительно оказываются по светимости ниже эддингтоновского предела для вращающихся звезд и, как правило, попадают ниже кривых, учитывающих поглощение гелием. Звезды типа Вольфа - Райе оказались выше эддингтоновского предела. Этого можно было ожидать, поскольку такие звезды нестационарны и здесь действительно есть истечение вещества. По-видимому, в потере массы этими звездами заметную роль играет и лучевое давление.
<< § 4.4 Звезды с лучистым переносом энергии | Оглавление | § 5.1 Пульсация переменных звезд >>