Глава VI. Автомодельные движения в звездах и межзвездном пространстве
Исследование движения газа в космических условиях представляет собой важный раздел современной астрофизики. Можно указать много проблем астрофизики, космогонии, космологии и т. д., требующих расчета характеристик движения газа. Проблема образования звезд, галактик, скоплений галактик требует решения задачи о коллапсе газовой массы под влиянием гравитационного притяжения. Теория эволюции звезд, в частности, появление вспышек новых и сверхновых, требует изучения образования и движения ударных волн в звездах. Исследование тесных двойных систем потребовало рассмотрения перетекания газовых потоков от одной звезды к другой. Таких примеров можно указать много.
Все это привело к тому, что возникла новая область астрофизики - космическая газодинамика (в том числе и ее раздел - межзвездная газодинамика). Уже появилось много обобщающих исследований и книг по этой проблеме, неоднократно созывались конференции (см. [1-6]).
Космическая газодинамика широко использует методы теории анализа размерностей и подобия. В этой главе мы рассмотрим лишь те задачи космической газодинамики, где эти методы являются основными. В силу обширности проблемы и ограниченности места мы не можем обсудить все задачи космической газодинамики, которые могут быть рассмотрены методами теории анализа размерностей и подобия, и ограничимся поэтому лишь некоторыми из них, которые по тем или иным причинам показались нам наиболее интересными.
Важно также отметить, что применение методов теории анализа размерностей и подобия к некоторым проблемам космической газодинамики было дано также в книгах Л. И. Седова [7] и К. П. Станюковича [8], где читатель может найти больше подробностей математического анализа этих проблем.
§ 6.1 Уравнения автомодельного движения космического газа
Очень простым является случай автомодельного (или самоподобного) движения газа. Здесь можно из соображений размерности получить общие характеристики движения, не прибегая к решению сложных уравнений движения. С другой стороны, рассматривая автомодельные движения, можно свести газодинамические уравнения в частных производных к системам более простых уравнений в обыкновенных производных, для которых к тому же могут быть сразу определены интегралы движения. Автомодельные движения, методы их исследования, соответствующие системы обыкновенных уравнений и методы их анализа подробно изложены в книге Л. И. Седова [7] и поэтому ограничимся лишь некоторым общим обсуждением применений метода автомодельных движений к проблемам астрофизики, а в последующих параграфах рассмотрим некоторые конкретные задачи, не затронутые в [7, 8].
Как это часто бывает в физике, наиболее простыми с точки зрения теоретического анализа являются одномерные движения - плоские, цилиндрически- или сферически-симметричные. Правда, методами теории автомодельных движений можно рассмотреть и более сложную геометрию, например, не только цилиндрически-симметричный случай, но также и движение с аксиальной симметрией. Однако мы здесь ограничимся случаем одномерных движений.
Действительно, несмотря на сложность движений в космических условиях, реальная геометрия в большинстве астрофизических задач все равно не может быть учтена в рамках той точности теории и наблюдений, которая нам доступна в настоящее время. Поэтому предположение о некоторой одномерной симметрии движений не очень мешает общности выводов и в то же время существенно упрощает математический анализ.
К тому же автомодельность движения имеет место только тогда, когда это движение характеризуется не более, чем двумя определяющими параметрами с независимыми размерностями. Поясним, что это значит. Движение газа определяется какими-то внешними или внутренними причинами. Например, оно может быть связано с нагреванием газа излучением - тогда определяющим параметром является поток лучистой энергии. Движение может быть вызвано внезапным освобождением большого количества энергии - взрывом. Мощность взрыва тогда тоже является определяющим параметром. Есть определяющие параметры, характеризующие начальное состояние газа, например, его плотность и давление.
Естественно, что движение космического газа характеризуется многими определяющими параметрами. Но часто можно выделить два основных, главных параметра с независимыми размерностями, которые определяют основные свойства движения - в этом случае задача становится автомодельной и ее можно исследовать относительно просто. Обозначим эти два основных определяющих параметра через А и В и, не ограничивая общности, можем принять для их размерностей (см. [7]):
|
|
(6.1) |
где k1, k2, k3, k4 - некоторые рациональные числа, которые могут быть и не целыми. Симметричное одномерное движение характеризуется координатой r и временем t. Из четырех размерных величин составляется одна безразмерная комбинация, которую мы запишем в виде
|
|
(6.2) |
где δ = -k3/k4.
Другие безразмерные комплексы образуем из параметров А, В и характеристик движения и состояния газа: скорости v, плотности ρ и давления р, а также координаты r. Составляя матрицу размерности с этими параметрами, находим три безразмерных комплекса:
|
|
(6.3) |
Значение этих комплексов мы обсудим ниже.
Наконец, приведем сами уравнения автомодельного движения. Для этого запишем уравнения симметричного движения политропного газа в простейшем случае, когда можно пренебречь гравитацией, магнитными полями и диссипативными эффектами [7]:
|
|
(6.4) |
|
|
(6.5) |
|
|
(6.6) |
Здесь γ - показатель политропного состояния, индекс ν характеризует симметрию движения: ν = 1 для плоских, ν = 2 для цилиндрически-симметричных и ν = 3 для сферически-симметричных движений. Заметим, что система (6.4) - (6.6) включает как частный случай и важные для астрофизики изотермические движения [5], где γ = 1.
Теперь перейдем в (6.4) - (6.6) к безразмерным функциям одного аргумента λ по формулам
|
|
(6.7) |
тогда получится система трех уравнений в обыкновенных производных по λ для функций V(λ), R(λ) и Р(λ). Мы эту систему записывать не будем, а сразу приведем ее в преобразованном виде, наиболее удобном для решения:
^2 - (\gamma - 1)V(V-1)(V-\delta)\}}{(V-\delta)[V(V-1)(V-\delta) + (\varkappa - \nu V)Z]} - \\ &-\frac{Z^2[2(V-1) + \varkappa(\gamma - 1)]}{(V-\delta)[V(V-1)(V-\delta) + (\varkappa - \nu V)Z]},
\end{array}
$$](https://images.astronet.ru/pubd/2013/03/01/0001281314/tex/formula717.gif)
|
(6.8) |
|
|
(6.9) |
|
|
(6.10) |
где
|
|
(6.11) |
а новая безразмерная функция
|
|
(6.12) |
есть квадрат безразмерной скорости звука (или безразмерной температуры).
Мы выписали систему уравнений (6.8) - (6.12) во всех деталях, поскольку в дальнейшем будет рассматриваться ее решение для некоторых частных случаев. Как уже отмечалось, система уравнений (6.8) - (6.12) получена и подробно исследована в наиболее общем виде Л. И. Седовым [7].
Сразу видно, что, по существу, здесь надо найти решение одного уравнения (6.8), т.е. найти зависимость Z от V. После этого уравнения (6.9) и (6.10) сводятся к квадратурам. Это особенно просто сделать для изотермического движения (γ = 1), которое будет подробно исследовано в следующем параграфе.
Теперь мы можем вернуться к общему обсуждению свойств автомодельного движения. Система (6.8) - (6.12) определяет однозначную зависимость безразмерных параметров движения Р, R, V и Z от λ . Пусть в некоторый момент времени t = t1 имеется определенное распределение этих параметров в пространстве, т. е. зависимость от координаты r (а следовательно, и от параметра λ (6.2)). В другой момент времени t = t1 это распределение будет другим, но подобным первому, поскольку зависимость от λ осталась неизменной. Условие подобия (или автомодельности) может быть записано как λ = const или
|
|
(6.13) |
Таким образом, решив систему (6.8) - (6.12) при соответствующих граничных условиях, мы получаем полную картину движения газа и распределение как в пространстве, так и во времени величин, характеризующих это движение (скорости, плотности и т.п.). Движение остается подобным самому себе и поэтому особенно удобно проследить за перемещением какой-либо экстремальной характеристики.
Например, как хорошо известно, при движении газа часто возникают разрывы - скачки плотности, скорости, температуры или ионизационные разрывы в межзвездном пространстве. На таких скачках терпят разрывы и безразмерные функции Р(λ), R(λ), V(λ) и Z(λ). Очевидно, что для сохранения автомодельности движения каждый разрыв должен характеризоваться определенным значением параметра λ . Таким образом, мы сразу получаем закон перемещения любого разрыва в автомодельном движении
|
|
(6.14) |
где λs = const. Величина Xs может быть определена при полном решении уравнений (6.8) - (6.12). Но даже и без точного численного определения величины Xs одно условие λs = const дает возможность изучить зависимость положения фронта разрыва от времени. Собственно, для астрофизических применений знание точного значения λs часто и не нужно вообще, поскольку численные значения определяющих параметров известны лишь приближенно, иногда даже с точностью до порядка величины. В этих случаях можно принять λs=1. Но в других случаях вычисление λs. необходимо. Такой случай, в частности, важен для расчета движения ионизационных разрывов в межзвездном пространстве (см. следующий параграф). Подробно методы вычисления скачков параметров и учет их в рамках теории автомодельного движения также изложены в [7].
Одним из первых успехов теории автомодельного движения было решение задачи о сильном взрыве. Это решение, полученное Л. И. Седовым в 1945 г. и использованное им для расчета расширения огненного шара атомного взрыва, было затем применено И. С. Шкловским (см. [9]) к анализу движения оболочки сверхновой II типа в межзвездной среде. Рассмотрим этот случай подробнее.
Пусть в однородной по плотности межзвездной среде расположена звезда, которая в начальный момент t=0 вспыхивает как сверхновая. Она сбрасывает оболочку, имеющую некоторую кинетическую энергию (с размерностью эрг = г ⋅ см2 ⋅ сек-2). Будем считать, что эта оболочка сферически-симметрична. Расширяясь, оболочка сверхновой вовлекает в движение межзвездный газ, передавая ему свою энергию. Скорость оболочки сверхновой на начальном этапе порядка 3-6 тысяч км/сек, т. е. больше скорости звука. Межзвездный газ, вовлекаемый в движение, тормозит оболочку, но еще долго скорость газа остается сверхзвуковой. Это означает, что передний фронт области движения газа представляет собой ударную волну, на которой имеет место скачок плотности, температуры и скорости.
Вообще говоря, характер движения существенно зависит от условия потерь энергии газа на излучение. Межзвездный газ, увлекаемый оболочкой сверхновой, нагревается и поэтому излучает энергию. Расчеты показывают, что особенно интенсивно это излучение при температуре газа около 105 градусов. При более низких температурах мала мощность механизмов теплового излучения газа, а при более высоких температурах водород и гелий уже ионизованы и эффективность потерь энергии опять уменьшается. При температурах порядка 105 градусов излучаются ультрафиолетовые спектры основных элементов.
Допустим теперь, что на переднем фронте движущейся области межзвездного газа скачок температуры настолько велик, что за этим фронтом температура поднимается много выше 105 градусов. Тогда излучение нагретого газа относительно невелико и можно считать, что при движении межзвездного газа и оболочки сверхновой сохраняется полная энергия взрыва Е, распределенная теперь между кинетической энергией вовлеченного в движение межзвездного газа и его тепловой энергией. Итак, один из определяющих параметров есть полная энергия Е, выделившаяся при вспышке сверхновой.
Остается выбрать еще один параметр. Очевидно, им может быть только плотность невозмущенного межзвездного газа ρ . Давлением невозмущенного межзвездного газа, а следовательно, и его температурой придется пренебречь. Это можно сделать, поскольку, по условию, температура за фронтом много больше 105 градусов, а температура межзвездного газа действительно много меньше этой величины. Учет "противодавления" (т. е. давления газа перед фронтом расширяющейся области) лишает рассматриваемую задачу условия автомодельности. Теория сильного взрыва с учетом противодавления подробно рассмотрена в книгах [7] и [10]. К астрофизическим задачам эта теория пока еще не применялась.
Итак, пока температура газа, вовлеченного в движение, велика, задача о движении оболочки сверхновой звезды в межзвездной среде имеет два определяющих параметра, которые мы выберем так:
|
|
(6.15) |
Сравнивая с изложенными выше соотношениями, мы можем принять А = ρ, т. е. k1 = -3 и k2 = 0, и В = Е/ρ, т. е. k3 = 5, k4 = -2 и δ = 2/5.
Из (6.15) сразу следует уравнение распространения переднего фронта области межзвездного газа, сжатого оболочкой сверхновой:
|
|
(6.16) |
где для простоты постоянная величина λs , принята равной единице. Тогда Е - это энергия вспышки сверхновой с точностью до некоторого численного множителя порядка единицы (для случая сильного взрыва в воздухе этот множитель равен 0,85 [7]).
Скорость движения фронта этой области
|
|
(6.17) |
К сожалению, мы не можем проследить за изменением скорости движения оболочки одной и той же сверхновой с течением времени или с увеличением ее расстояния от центра из-за "недостатка" времени. Но можно проверить применимость соотношения (6.17) статистическим методом.
Для примера приведем графики Т. А. Лозинской [11], на которых для ряда туманностей - остатков сверхновых - нанесены зависимости величин ![]() как от времени t (рис. 22, а), так и от величины
как от времени t (рис. 22, а), так и от величины ![]() (рис. 22, б). Если бы все вспышки сверхновых были связаны с освобождением одной и той же энергии Е, то согласно (6.17) все характерные точки оказались бы на одной прямой в соответствии с условием vудρ1/5t3/5 = const или
(рис. 22, б). Если бы все вспышки сверхновых были связаны с освобождением одной и той же энергии Е, то согласно (6.17) все характерные точки оказались бы на одной прямой в соответствии с условием vудρ1/5t3/5 = const или ![]() = const. Естественно, что имеется разброс величины Е, но из этих графиков видно, что все же существует определенная концентрация к двум прямым. Наличие двух прямых отражает существование двух типов сверхновых с различным характером взрывов. Характерные величины энергий вспышек следующие: для более мощных сверхновых (так называемых сверхновых II типа, дающих туманности вида Петли в Лебеде или источника Кассиопея А) величина Е ≈ 1051 эрг; у более слабых сверхновых I типа (давшей, например, Крабовидную туманность) Е ≈ 1048 эрг.
= const. Естественно, что имеется разброс величины Е, но из этих графиков видно, что все же существует определенная концентрация к двум прямым. Наличие двух прямых отражает существование двух типов сверхновых с различным характером взрывов. Характерные величины энергий вспышек следующие: для более мощных сверхновых (так называемых сверхновых II типа, дающих туманности вида Петли в Лебеде или источника Кассиопея А) величина Е ≈ 1051 эрг; у более слабых сверхновых I типа (давшей, например, Крабовидную туманность) Е ≈ 1048 эрг.
Эти оценки также получаются из формулы (6.17), если ее применить для отдельных туманностей с известными параметрами. Например, для туманности Петля в Лебеде имеем vуд ≈ 100 км ⋅ сек-1, ρ = 10-23 г ⋅ см-3, rуд = 20 пс, откуда и находим Е ≈ 1051 эрг. Кстати, эту же формулу можно использовать и для оценки времени существования туманности. Получаем t ≈ 3 ⋅ 104 лет.
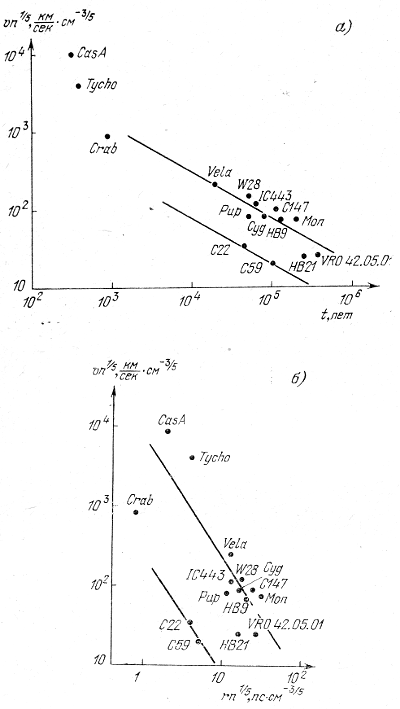
Рис. 22. Зависимость скорости расширения оболочки сверхновых от времени (а) и от размера туманности - остатка сверхновой (б) (согласно Т. А. Лозинской).
Заметим, что при цилиндрическом и линейном разлете оболочки светимость падала бы значительно медленнее, как L ∼ t-4/5 и L ∼ t-2/5 соответственно. Поэтому образование волокон на более поздней стадии расширения благоприятствует более длительному сохранению свечения; в этом, возможно, и заключается ответ на известный вопрос Г. А. Шайна - почему на небе так много волокнистых туманностей?
Вернемся к анализу автомодельной задачи. Решение уравнений (6.8) - (6.12) для данного случая позволяет определить распределение температуры и плотности за передним фронтом движущегося газа. Точные решения для разных значений γ приведены в [7]. Мы здесь опишем их только качественно. На фронте ударной волны движущегося газа плотность скачком возрастает до величины ρ2, где
|
|
(6.18) |
(при γ = 5/3 - в четыре раза). Температура газа равна
|
|
(6.19) |
где μ молекулярный вес, ℜ - универсальная газовая постоянная, vуд скорость ударной волны. Во втором равенстве принято γ = 5/3 и использована вторая формула (6.17). Сразу же за фронтом ударной волны плотность газа быстро спадает, а температура растет еще больше, так что давление газа сначала несколько уменьшается (примерно в два раза), а потом остается постоянным по всей внутренней области, охваченной движением.
Поскольку интенсивность излучения нагретого газа при Т ≈ 105 градусов спадает как с уменьшением плотности, так и с увеличением температуры, то это означает, что электромагнитное излучение (преимущественно в рентгеновском и ультрафиолетовом диапазонах) генерируется только в очень узком слое, прилегающем к переднему фронту движущегося газа. Вероятно, относительная толщина излучающей области порядка 1/10 радиуса переднего фронта.
По мере расширения области движущегося межзвездного газа температура T2 падает, и когда она окажется меньшей 105 градусов, излучение станет весьма эффективным. Здесь уже значительная - часть энергии теряется на излучение и мы не можем больше считать полную энергию E сохраняющимся, а следовательно, и определяющим параметром.
Но не только потери энергии на излучение ограничивают применимость этого решения. Дело в том, что здесь предполагается, что ударная волна в межзвездной среде образуется сразу же после взрыва и начала движения оболочки сверхновой. На самом деле это не так, поскольку в реальной межзвездной среде определенную роль играют различные диссипативные коэффициенты и образование ударной волны происходит лишь через некоторое время после начала движения оболочки.
В работе В. Ф. Дьяченко, В. С. Имшенника и В. В. Палейчика [13] было получено численное решение следующей задачи. В водородной полностью ионизованной плазме в некоторый момент времени начинает двигаться с постоянной скоростью сферический поршень. Решалась система уравнений, описывающая как ионную, так и электронную компоненту плазмы с учетом бесстолкновительных процессов, вязкости и теплопроводности обоих компонент и обмена энергией между нами.
Начальная стадия движения оболочки не имеет газодинамического характера и ударная волна образуется лишь через некоторое время, определенное вязкостью протонной компоненты плазмы. Как было показано в работе [13], ударная волна образуется через время t0 после взрыва, где
|
|
(6.20) |
Здесь v0 - начальная скорость оболочки, mp и е - масса и заряд протонов, Λ ≈ 30-70 - кулоновский логарифм.
Начальные скорости оболочек сверхновых могут достигать значения ∼ 5 ⋅ 103 км/сек. При плотности межзвездной среды ρ ≈ 10-23 г/см³ можно получить из (6.20) оценку времени образования ударной волны ∼ 3 ⋅ 106 лет. Можно поставить вопрос иначе - какая должна быть скорость оболочки, при которой ударная волна образуется, например, через 104 лет после вспышки сверхновой? Дело здесь в том, что, как показывают наблюдения, оболочка сверхновой в Крабовидной туманности совсем не затормозилась, хотя эта сверхновая вспыхнула уже 103 лет назад. С другой стороны, оболочка туманности Петли в Лебеде затормозилась очень сильно. Эта сверхновая вспыхнула, вероятно, около 105 лет назад. Полагая в (6.20) v0 ≈ 104 лет, находим t0 103 км/сек.
По-видимому, сразу после вспышки сверхновой образуется тепловая волна в межзвездном газе. Вероятно, здесь имеет место бесстолкновительная диссипация энергии и оболочка тормозится не газодинамическим путем. Лишь после того как скорость оболочки уменьшится до v ∼ 103 км/сек, начнется торможение путем образования ударной волны и, начиная с этого времени, можно применять решение задачи о сильном взрыве.
Несколько лучше обстоит дело в случае движения оболочек новых звезд в плотной межзвездной среде. Здесь время образования ударной волны всего несколько десятков лет.
После того как значительная доля энергии, как оболочки, так и нагретой межзвездной среды, высветилась из-за излучения в ультрафиолетовой и рентгеновской области спектра, расширение не останавливается.
Более того, последние данные о рентгеновских источниках показывают, что вокруг видимых в оптике некоторых туманностей, остатков сверхновых, наблюдаются большие по размеру области довольно интенсивного рентгеновского излучения. Напомним, что графики рис. 22 построены по данным оптических наблюдений и, следовательно, они определяют скорость разлета более плотных, но низкотемпературных областей. Менее плотные, но более нагретые области сжатого межзвездного газа расширится с большей скоростью, несмотря на заметную потерю энергии на излучение.
При интенсивном излучении расширение оболочки и сжатой области межзвездного газа определяется уже не полной энергией взрыва, а количеством движения оболочки. Из уравнений сферически-симметричного движения газа можно получить следующий строгий закон изменения количества движения:
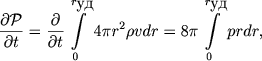
|
(6.21) |
где ![]() полное количество движения оболочки и межзвездного газа*). Если из-за высвечивания давление газа внутри области, охваченной движением, очень быстро уменьшается и падает до нуля, то можно считать количество движения оболочки
полное количество движения оболочки и межзвездного газа*). Если из-за высвечивания давление газа внутри области, охваченной движением, очень быстро уменьшается и падает до нуля, то можно считать количество движения оболочки ![]() сохраняющейся величиной и принять
сохраняющейся величиной и принять ![]() в качестве определяющего параметра вместо энергии вспышки.
в качестве определяющего параметра вместо энергии вспышки.
Тогда закон распространения переднего фронта расширяющейся области межзвездного газа имел бы такой вид:
|
|
(6.22) |
Как легко показать, если повторить все приведенные выше рассуждения и учесть, что теперь в определяющем параметре ![]() , мы имеем k3 = 4, k4 = -1.
, мы имеем k3 = 4, k4 = -1.
Скорость переднего фронта этой области
|
|
Как и следовало ожидать, здесь торможение более быстрое. Впрочем, вероятно, это решение имеет очень ограниченную область применения, поскольку оно требует, как уже отмечалось, обращения в нуль правой части (6.21). Маловероятно, чтобы в реальных астрофизических условиях высвечивание газа было бы настолько сильным, что давление межзвездной среды в области вспышки было бы очень малым. Напомним, что, как показывают наблюдения, при вспышках сверхновых образуется большое количество релятивистских электронов, давление которых отнюдь не мало.
К автомодельным движениям относится случай разлета газа в пустоту, который также может найти применение в астрофизике. Предположим, что у ограниченного объема газа с равномерной плотностью и температурой внезапно удалили стенку. Тогда по газу внутрь побежит волна разрежения, а с открытой стороны начнется истечение. Если нет противодавления извне, то определяющими параметрами будут плотность газа ρ и скорость звука ![]() где T0 - температура газа до удаления стенки. Здесь параметр В можно приравнять v и, следовательно, движение описывается соотношением
где T0 - температура газа до удаления стенки. Здесь параметр В можно приравнять v и, следовательно, движение описывается соотношением
|
|
(6.23) |
Для переднего фронта разлетающегося газа в плоском случае (одномерном движении вдоль одной координаты) имеем λ = 2(γ - 1)-1. Для цилиндрически- и сферически-симметричных движений простых аналитических формул получить не удавалось, но было показано, что по крайней мере при γ = 3 также λ = 1 [8], так что можно считать условие для скорости переднего фронта разлетающегося газа
|
|
(6.24) |
достаточно общим. Предположение о том, что газ разлетается в пустоту со скоростью в три раза большей скорости звука в покоящейся среде, часто используется в астрофизике.
Автомодельный метод был применен Г. С. Бисноватым-Коганом, Я. Б. Зельдовичем и Д. К. Надежиным [14] и для анализа обратной задачи - аккреции газа на звезду. Если считать, что масса аккрецирующего газа много меньше массы самой звезды, то остаются два определяющих параметра - ускорение силы тяжести g и начальная плотность аккрецирующего газа. При набегании газа на звезду на некотором расстоянии от нее образуется ударная волна, уходящая от ее поверхности. Основной задачей является определение скорости движения этой ударной волны. Здесь безразмерный аргумент
|
|
(6.25) |
На фронте ударной волны должно быть λ = λуд = const. Поэтому ударная волна ускоряется по мере удаления от поверхности звезды, на которую выпадает аккрецирующий газ:
|
|
(6.26) |
Разумеется, это формула справедлива, пока g считается постоянной, т. е. пока ударная волна не отойдет от звезды на расстояние, сравнимое с ее радиусом. Величину λуд можно определить только путем численного решения автомодельных уравнений движения. В работе [14] были получены значения: λуд = 0,3154 при γ = 5/3 и λуд = 0,1521 при γ = 4/3. Масса газа, заключенная между поверхностью звезды и ударной волной, увеличивается со временем как ¼ξρgt, где численное значение множителя ξ = 2,256 при γ = 5/3 и ξ = 2,075 при γ = 4/3.
Авторы работы [14] отмечают, что если допустить, что аккрецирующий газ беспрепятственно проваливается под поверхность звезды ("черная дыра"), то ξ = 2.
*) Формула (6.21) получена В. С. Имшенником.
<< § 5.4 Циркуляция в атмосферах планет | Оглавление | § 6.2 Ионизационные фронты и ударные волны высвечивания в межзвездном пространстве >>