§ 6.2 Ионизационные фронты и ударные волны высвечивания в межзвездном пространстве
Ионизационные фронты представляют собой специфическое явление межзвездной газодинамики, не имеющее аналога в земных условиях. Напомним физическую картину этого явления. Пусть горячая звезда с интенсивным потоком ультрафиолетового излучения, способного ионизовать водород, находится в области, заполненной межзвездным газом. В окружающей звезду области водород ионизован почти полностью - это так называемая зона Стремгрена Н II, рассматриваемая еще в гл. 1. Вдали от горячей звезды межзвездный водород остался неионизованным - это область Н I. Можно показать, что граница между зонами Н II и Н I сравнительно узкая, ее толщина составляет не более нескольких процентов от радиуса зоны Стремгрена (см., например. [15]). Поэтому границу между зонами Н I и Н II можно рассматривать как некоторый фронт, на котором температура и степень ионизации меняются скачком. В зонах Н I водород полностью нейтрален и, вероятнее всего, находится в молекулярном состоянии. Здесь температура газа порядка или меньше 100 њК в более плотных областях и может быть несколько выше, до 103 њК, в разреженных областях. В зонах Н II водород почти полностью ионизован и температура газа здесь 8000 - 10 000њ.
Таким образом, по обе стороны ионизационного фронта давление газа неодинаково, что должно приводить к движению ионизационного фронта в сторону зоны Н I. Кроме того, со стороны горячей звезды на ионизационный фронт все время падает поток ионизующих квантов. Это означает, что через ионизационный фронт все время перетекает газ из области Н I в область Н II. Исследование динамики этого перетекания (или, что одно и то же, движения ионизационного разрыва в сторону Н I) и составляет один из важных разделов межзвездной газодинамики. В частности, здесь нашли применение и методы теории автомодельного движения. Мы не будем рассматривать все вопросы теории ионизационных фронтов (см. [5, 15, 16]), а ограничимся лишь обсуждением применения методов теории автомодельного движения. Однако прежде нам понадобятся некоторые соотношения как общей теории ударных волн с высвечиванием, так и теории ионизационных фронтов.
Начнем с теории ударных волн с высвечиванием (см. [5]). Рассмотрим такую картину движения. Пусть в области неподвижного холодного газа с температурой T1 движется сильная ударная волна, сжимающая газ и нагревающая его до некоторой высокой температуры T2*. Если T2* порядка (или не намного выше) температуры 103 градусов, то в сжатой и нагретой области ударной волны возникает сильное излучение, быстро охлаждающее газ. Из-за этого газ в ударной волне продолжает сжиматься, что еще больше его охлаждает. Наконец, при некоторой температуре T2 интенсивное излучение может заметно уменьшиться и газ опять придет в некоторое, вообще говоря, новое состояние теплового равновесия. Температура T2 может быть и равна T1, если физическое состояние газа не очень изменилось (например, если в ударной волне не меняется состояние ионизации и диссоциации молекул). Однако обычно в ударной волне происходят необратимые изменения и поэтому новая равновесная температуры T2 вероятно, заметно больше T1.
Предположим, что вся картина рассмотренного движения стационарна. Тогда из условия сохранения массы и потока импульса газа при протекании его через область сжатия и высвечивания можно получить два соотношения, связывающие изменение плотности газа и его скорости по обе стороны этой области. Напомним, что в силу высвечивания поток энергии не сохраняется.
Условия сохранения потока массы и импульса имеют вид
|
|
(6.27) |
|
|
(6.28) |
где ρ1 и ρ2 - плотность газа до и после фронта волны, v1 - скорость втекания газа в область сжатия и высвечивания, v2 - скорость его вытекания из этой области. Поскольку состояние газа меняется, то молекулярные веса μ1 и μ2 могут быть различными. Следует подчеркнуть, что в этом параграфе под v всегда понимается скорость газа по отношению к фронту разрыва.
Если считать, что ударная волна сжатия и высвечивания движется в неподвижном газе и что скорость ударной волны задана, то в (6.27) - (6.28) следует считать ρ1, v1, T1/μ1 и T2/μ2 заданными и тогда эта система определяет ρ2 и v2. Решение системы (6.27) - (6.28) очевидно:
![$$
\begin{array}{ll}
\frac{\rho_1}{\rho_2} = \frac{v_2}{v_1} = &\frac{1}{2} \left[1 + \frac{\Re T_1}{\mu_1 v_1^2} \pm \sqrt{\left(1 + \frac{\Re T_1}{\mu_1 v_1^2}\right)^2 - \frac{4\Re T_2}{\mu_2 v_1^2}}\right] \approx \\
& \approx \frac{1}{2} \left(1 \pm \sqrt{1 - \frac{4\Re T_2}{\mu_2 v_1^2}} \right).
\end{array}
$$](https://images.astronet.ru/pubd/2013/03/01/0001281314/tex/formula797.gif)
|
(6.29) |
В последнем равенстве учтено, что в сильных ударных волнах с высвечиванием скорость ударной волны v1 много больше скорости звука в покоящемся газе v1s = (γT1/μ1)½. Можно также убедиться, что и член ![]() мал по сравнению с единицей. В самом деле, максимальная температура в области сжатия T2* порядка кинетической энергии волны, отнесенной к одной частице, т. е.
мал по сравнению с единицей. В самом деле, максимальная температура в области сжатия T2* порядка кинетической энергии волны, отнесенной к одной частице, т. е. ![]() . Если высвечивание заметно, то T2 ≪ T2* и поэтому вместо (6.29) можно написать два решения в виде
. Если высвечивание заметно, то T2 ≪ T2* и поэтому вместо (6.29) можно написать два решения в виде
|
|
(6.30) |
|
|
(6.31) |
Второе решение соответствует слабой волне сжатия с высвечиванием малой амплитуды и в дальнейшем рассматриваться не будет.
Решение (6.30) описывает сильную волну уплотнения (ρ2 ≫ ρ1) с высвечиванием газа. Мы не будем рассматривать структуру ударной волны с высвечиванием (см., например, [5, 12, 13]), отметим лишь, что подавляющая часть потока кинетической энергии в сильной ударной волне
|
|
(6.32) |
превращается в излучение и уходит из области сжатия. По формуле (6.32) можно сразу определить поток полного (проинтегрированного по всему спектру) излучения фронта ударной волны с высвечиванием.
Теперь перейдем к ионизационным фронтам. Здесь есть много общего с ударными волнами с высвечиванием, хотя структуры такой ударной волны и ионизационного фронта существенно различаются. Мы обсудим это различие подробнее ниже, а сейчас ограничимся некоторыми общими замечаниями. Неионизованный газ, втекая в область ионизационного фронта, поглощает ионизующие кванты, при этом ионизуется и нагревается. Затем начинается высвечивание тепловой энергии и температура опять падает уже в области почти полной ионизации. Окончательная температура за фронтом ионизационного фронта, для которой мы сохраним обозначение T2, также определена условием равновесия с излучением.
Это означает, что система (6.27) и (6.28) справедлива и для ионизационных фронтов с тем существенным дополнением, что поток массы через ионизационный фронт теперь определен потоком ионизующих квантов. В самом деле, число атомов водорода, пересекающих ионизационный фронт, должно равняться числу ионизующих квантов, попадающих на этот фронт из области Н II. Поэтому вместо (6.27) теперь запишем
|
|
(6.33) |
где mH - масса атома водорода, а J - поток ионизующих квантов на единицу поверхности ионизационного фронта. Система уравнений (6.28) и (6.33) определяет свойства ионизационных фронтов. Отличие от ударной волны с высвечиванием заключается в том, что теперь скорость v1 движения ионизационного фронта по неионизованному газу определяется потоком ионизующих квантов:
|
|
(6.34) |
где nH - концентрация атомов водорода в зоне Н I. Решение (6.29) остается справедливым и здесь, только теперь нельзя считать величины ![]() или
или ![]() , малыми при любых условиях.
, малыми при любых условиях.
Из требования вещественности (6.29) следует ограничение
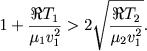
|
(6.35) |
Отсюда следуют условия, налагаемые на скорость ионизационного фронта относительно газа в Н I. Из (6.35) находим, что неравенство выполняется, если
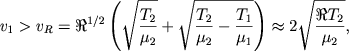
|
(6.36) |
либо если
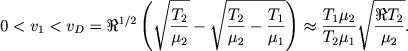
|
(6.37) |
Здесь vR и vD - значения скоростей ионизационных фронтов, ограничивающие разные режимы течения газа.
Комбинируя неравенства (6.36) и (6.37) с соотношением (6.34), находим условия образования ионизационных фронтов при заданном потоке ионизующих квантов J и плотности газа в зоне Н I. Эти условия отражены в классификации ионизационных фронтов по Кану [17].
1. Ионизационный фронт R-типа, распространяющийся в разреженной области Н I. Условие на плотность газа имеет вид
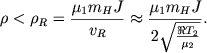
|
(6.38) |
При этом из (6.29) следует, что возможны два типа R-фронта. В одном из них газ в Н I оттекает от фронта со сверхзвуковой скоростью, т. e. ![]() , а в другом типе R-фронта
, а в другом типе R-фронта ![]() . Принято называть первый случай сильным R-фронтом, а второй случай - слабым R-фронтом. И в том и в другом случае плотность газа при прохождении ионизационного фронта увеличивается.
. Принято называть первый случай сильным R-фронтом, а второй случай - слабым R-фронтом. И в том и в другом случае плотность газа при прохождении ионизационного фронта увеличивается.
2. Критический ионизационный фронт R-фронта, при котором v2 = vR и неравенство (6.38) заменяется на равенство. За ионизационным фронтом ![]() - это известное в газодинамике условие точки Жуге. В критическом ионизационном фронте R-типа также имеет место уплотнение газа. Здесь важно то, что отток газа в Н II от фронта происходит с местной изотермической скоростью звука, но зато этот фронт при заданном J может распространяться только в среде с фиксированной плотностью ρR.
- это известное в газодинамике условие точки Жуге. В критическом ионизационном фронте R-типа также имеет место уплотнение газа. Здесь важно то, что отток газа в Н II от фронта происходит с местной изотермической скоростью звука, но зато этот фронт при заданном J может распространяться только в среде с фиксированной плотностью ρR.
3. Ионизационный фронт D-типа, распространяющийся в более плотной области неионизованного газа. Условие на плотность газа в Н I имеет вид
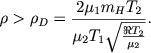
|
(6.39) |
Здесь также имеют место два типа D-фронтов: сильный фронт, в котором ![]() и слабый фронт с
и слабый фронт с ![]() . В обоих случаях на ионизационных фронтах D-типа происходит разрежение плотного газа при попадании его в область Н II.
. В обоих случаях на ионизационных фронтах D-типа происходит разрежение плотного газа при попадании его в область Н II.
4. Критический фронт D-типа, при котором v2 = vD и неравенство (6.39) превращается в равенство. Здесь также выполнено условие точки Жуге: и ![]() , и критические фронты D-типа при заданном значении потока ионизующих квантов могут распространяться лишь в области Н II с фиксированной плотностью ρD.
, и критические фронты D-типа при заданном значении потока ионизующих квантов могут распространяться лишь в области Н II с фиксированной плотностью ρD.
5. Ионизационные фронты М-типа, которые распространяются в зоне Н I с плотностью среды
|
|
Из изложенного выше ясно, что ионизационные фронты М-типа в чистом виде существовать не могут. Перед ионизационным фронтом такого типа движется либо волна уплотнения, увеличивающая плотность газа в Н I до ρ > ρD, либо волна разрежения, понижающая плотность газа в Н I до ρ < ρR.
Надо отметить, что по мере перемещения в однородной области Н I тип ионизационного фронта может изменяться, поскольку при этом меняется и величина потока ионизующих квантов. При удалении от звезды поток уменьшается как J ∼ r2, но величина J может меняться и за счет эволюции звезды - с течением времени меняются светимость и поверхностная температура. Кроме того, с удалением фронта растет и поглощение этих квантов. По-видимому, при возгорании горячей звезды в области неионизованного водорода сначала при большом J образуется близкий к звезде ионизационный фронт сильного R-типа. Затем он переходит в критический фронт R-типа. Здесь заканчивается формирование обычной зоны Н II. Ее граница продолжает расширяться в области Н I, создавая впереди ударную волну, а затем, по мере падения J, ионизационный фронт приобретает характеристики D-типа [15].
Детальная структура ионизационных фронтов рассматривалась во многих работах (обзор см. в [16]). В частности, в работе [18] было получено уравнение, определяющее температуру T2 по заданной температуре ионизующей звезды T∗, если считать, что спектральное распределение потока ионизующих квантов J описывается формулой Планка с Т = T∗. Для T2 в градусах Кельвина имеем уравнение:
|
|
(6.40) |
При изменении T∗ от 20 до 80 тысяч градусов величина T2 меняется от 6500 до 9400 њК.
Основной проблемой теории ионизационных фронтов является расчет их движения в межзвездной среде. В наиболее простой постановке задача заключается в следующем. Пусть в однородной зоне Н I вспыхнула горячая звезда. Сначала волна ионизации распространяется быстро и нет заметных газодинамических эффектов. Через какое-то время на некотором расстоянии от звезды образуется квазистационарный ионизационный фронт, который затем относительно медленно продвигается внутрь области Н I. Это движение мы и будем рассматривать, использовав методы теории автомодельного движения. Разумеется, эти методы дают только ограниченные результаты, но, как оказалось, они качественно согласуются и с результатами, полученными при более точных численных расчетах. Обзор различных методов расчета движения ионизационных фронтов дан в работе [19].
Применение метода автомодельных движений к ионизационным фронтам было дано С. А. Капланом [5]. Эта задача также рассматривалась в работах [20-23]. Наиболее полные численные решения даны в работах [23, 24].
Для автомодельности движения необходимо иметь только два основных определяющих параметра. Один из них очевиден - это плотность газа в области Н I, обозначаемая в дальнейшем как ρ1 Вторым параметром, вообще говоря, можно выбрать светимость звезды в диапазоне частот ионизующих квантов. Так и сделано в работах [20, 21]. Однако, поскольку при этом поток прямых (т. е. идущих от звезды) ионизующих квантов падает как r-2 по мере распространения ионизованного фронта, то для сохранения автомодельности приходится допускать определенную зависимость плотности в Н I от расстояния до звезды и рассматривать цилиндрически-симметричную задачу.
В работе [22] сохранена сферическая симметрия и постоянная начальная плотность, но предположено, что ионизующая светимость звезды растет со временем как t3.
Строго говоря, у нас нет оснований считать полную мощность ионизующих квантов, падающих изнутри на весь ионизационный фронт, некоторой фиксированной величиной - постоянной или меняющейся со временем определенным образом. Кроме прямых ионизующих квантов от звезды есть еще и диффузные ионизующие кванты, количество которых также может меняться с изменением геометрии зоны НИ или со временем. По нашему мнению, более характерным определяющим параметром является температура T2 на внутренней границе ионизационного фронта, более или менее однозначно, как следует из (6.40), определенная поверхностной температурой ионизующей звезды T∗.
С другой стороны, поток ионизующих квантов, по существу, определяет сам характер ионизационного фронта и не учитывать эту величину при анализе движения ионизационного фронта нельзя. Это означает, что в действительности исследование движения ионизационного фронта не сводится строго к автомодельной задаче. Тем не менее мы рассмотрим движение ионизационного фронта как автомодельную задачу, поскольку в этом случае можно получить хотя и не точные, но зато физически наглядные решения.
В соответствии с предположением об автомодельности будем считать определяющими параметрами две величины, постоянство которых во времени наиболее четко выражено. Это плотность газа ρ и температура T∗. Очевидно, что заданными можно считать плотность и температуру в невозмущенной зоне Н I, т. е. величины ρ1 и T1. По условию, можно считать заданной и температуру в зоне Н II, т. е. величину T2 (определенную, например, уравнением (6.40)). Но, кроме того, можно задать еще некоторые значения параметров в зоне Н II.
Не очень ясно, насколько можно требовать выполнения условия точки Жуге за ионизационным фронтом (см. [5]). Это условие сводится к предположению, что ионизованный газ оттекает свободно от ионизационного фронта, - т. е. его движению не мешает сама зона Н II. Тогда скорость газа по отношению к ионизационному фронту равна местной скорости звука, т. е. ![]() , и ионизационная волна оказывается критическим фронтом R- или D-типа. При этом однозначно определены скорости ионизационного фронта относительно газа перед фронтом, согласно формулам (6.36) или (6.37), а также все другие параметры ионизационной волны, как, например, скачок плотности.
, и ионизационная волна оказывается критическим фронтом R- или D-типа. При этом однозначно определены скорости ионизационного фронта относительно газа перед фронтом, согласно формулам (6.36) или (6.37), а также все другие параметры ионизационной волны, как, например, скачок плотности.
Но условие точки Жуге является обязательным, если ионизованный газ оттекает от ионизационного фронта в пустоту. Если же внутри зоны Н II уже имеется достаточно ионизованного газа, в котором скорость звука не мала (∼ 10 км/сек), то плотность газа, а следовательно, и давление внутри зоны Н II успевает выровняться так, что газ оттекает от ионизационного фронта с некоторой меньшей скоростью, т. е. ионизационный разрыв может быть и сильного и слабого R- или D-типов. Усложняет задачу и то, что величина J определяется полным потоком ионизующих квантов, как прямых идущих от звезды, так и диффузных, рассеянных в самой зоне II II и достигающих границы этой зоны.
Разумнее всего считать, что на внутренней стороне ионизационного фронта заданы плотность газа ρ2, температура T2 и что нам известна скорость оттока газа v2, определенная по соотношению типа (6.34):
|
|
(6.41) |
где J - поток ионизующих квантов па внутренней стороне ионизационного фронта и np - концентрация протонов (или электронов) в этой области. Если vt есть скорость ионизационного фронта в пространстве, то скорость газа за фронтом этой волны в неподвижной системе координат есть v2 - vi. Заметим, что величины ρ2, T2 и v2 - vi могут быть в принципе определены независимо друг от друга по данным наблюдений.
Уравнение для определения скачков параметров на фронте ионизационного разрыва тождественно с уравнением (6.29), поскольку и здесь исходная система совпадает с (6.27) - (6.28). Напомним, что гее различие сводится к заданию величины потока ионизующих квантов через этот фронт. Напомним также, что скорости v1 и v2есть скорости газа по отношению к фронту ионизационного разрыва (v1 - в Н I и v2 в Н II).
Теперь перейдем к формулировке самой автомодельной задачи для анализа движения ионизационного фронта. Согласно сказанному выше определяющими параметрами будут:
![$$
[A] = [\rho_2] = \mbox{г} \cdot \mbox{см}^{-3}; \quad [B] = \left[\sqrt{\frac{\Re T_2}{\mu_2}}\right] = \mbox{см} \cdot \mbox{сек}^{-1}.
$$](https://images.astronet.ru/pubd/2013/03/01/0001281314/tex/formula818.gif)
|
(6.42) |
Сопоставляя (6.1) и (6.2), получаем значения показателей k1 = -3, k2 = 0, k3 = 1, k1 = -1, δ = 1. Параметр ϰ согласно (6.11) равен нулю. Поскольку температура считается определяющим параметром, то движение можно считать изотермическим, следовательно, примем γ = 1. И действительно, как в зонах Н I, так и в зонах Н II существенную роль играет взаимодействие с излучением и поэтому температура действительно определяется в первую очередь балансов поглощения и излучения лучистой энергии.
При этих условиях автомодельные уравнения движения (6.8) - (6.10) оказываются элементарно простыми:
|
|
(6.43) |
где
|
|
(6.44) |
Прежде чем идти дальше, сделаем одно замечание. В общих уравнениях автомодельных движений (6.8) - (6.10) есть особая точка, в которой выполняется условие Z = (V - δ)². В случае (6.43) условие особой точки: Z = (V - 1)². Для строго плоского движения (т. е. при ν = 1) эта особая точка превращается в особое решение, поскольку здесь и числители второго и третьего уравнений (6.43) обращаются в нуль. Решение Z = (V - 1)² исследовано в [5]. Однако для неплоских движений условие Z = (V - 1)² уже не является особым решением, а лишь особой точкой. Поскольку реальная структура ионизационного фронта не. описывается строго одномерным решением, то это особое решение есть вырожденный случай и вряд ли осуществляется в действительности. Здесь это решение рассматриваться не будет.
Из (6.43) следует, что для плоского одномерного движения (ν = 1) неособое решение находится сразу:
|
|
(6.45) |
где константы определяются граничными условиями. При этом нужно иметь в виду, что (6.45) справедливо только для области непрерывного течения и что на ионизационном разрыве и на фронте ударной волны значения констант в (6.45) также меняются скачком.
Обозначим через λi значение параметра λ на фронте ионизационного разрыва, т. е. будем считать скорость ионизационного фронта в пространстве равной
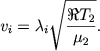
|
(6.46) |
Рассмотрим сначала простейшую задачу. Пусть по газу в зоне Н I с плотностью ρ1 движется одиночный ионизационный разрыв. Поскольку плотность в Н II тоже задана, то известен скачок плотности
|
|
(6.47) |
Согласно условию (6.41) мы знаем и величину v2, а следовательно, и величину V2(λi) для безразмерной скорости в неподвижной системе координат. Отсюда имеем
![$$
v_2 = v_i - \frac{r}{t}V_2(\lambda_i) = \sqrt{\frac{\Re T_2}{\mu_2}}\lambda_i [1-V_2(\lambda_i)],
$$](https://images.astronet.ru/pubd/2013/03/01/0001281314/tex/formula823.gif)
|
(6.48) |
если, конечно, определена величина λi. Для ее нахождения воспользуемся условием (6.29), которое в безразмерных переменных приобретает вид
![$$
R_1(\lambda_i) = 1 - V(\lambda_i) = \frac{1}{2}\left[1 + \frac{\mu_2 T_1}{\mu_1 T_2}\frac{1}{\lambda_i^2} \pm \sqrt{\left(1 + \frac{\mu_2 T_1}{\mu_1 T_2}\frac{1}{\lambda_i^2}\right)^2 - \frac{4}{\lambda_i^2}}\right].
$$](https://images.astronet.ru/pubd/2013/03/01/0001281314/tex/formula824.gif)
|
(6.49) |
Мы имеем два уравнения, каждое из которых независимо определяет V2(λi) и λi. Ясно, что полученные таким образом значения величин, как правило, не будут удовлетворять (6.48) для заданного значения v2. Задача оказалась переопределенной.
Выходов из этого затруднения два. Например, можно было бы считать, что параметры зоны Н II произвольны, т. е. неизвестны по отдельности ρ2 и v2 (но, по-прежнему, задано их произведение (6.41)). Тогда (6.49) следует рассматривать как два уравнения, определяющие R1(λi) и V2(λi). Для нахождения λi запишем (6.41) в безразмерном виде:
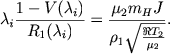
|
(6.50) |
Подставляя сюда V(λi) и R1(λi) из (6.49), находим λi.
Однако этот случай осуществляется, вероятно, редко. Более вероятен второй случай, когда ионизационный фронт создает перед собой ударную волну, сжимающую газ в зоне Н I так, чтобы по ней уже могла бы распространяться ионизационная волна с параметрами, определенными ионизующей звездой заданного типа.
Здесь могут быть различные комбинации движении, но мы рассмотрим простой и весьма вероятный случай, когда ионизующая звезда создает расширяющуюся оболочку в области Н I. На переднем фронте этой оболочки идет ударная волна, сжимающая газ в Н I, а ее задний фронт представляет собой ионизационный фронт D-типа, на котором происходит разрежение и ионизация газа. Такие оболочки действительно часто наблюдаются вокруг зон Стремгрена, созданных очень горячими звездами. Структура таких оболочек рассматривалась в работах [5, 23, 24]. Для анализа этой задачи мы и используем описанный выше автомодельный метод.
Пусть положению ударной волны соответствует значение λs, т. е. ее скорость движения по неподвижному газу Н I есть
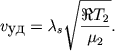
|
(6.51) |
Очевидно, что λs > λi и область λs - λi соответствует сжатой движущейся оболочке газа Н I. Ради простоты будем считать, что температура T'1 в этой оболочке равна температуре T1 в невозмущенной области Н I. Это ограничение не обязательно и в книге [5] рассмотрено условие T'1 > T1. Штрихованными величинами будем обозначать значения параметров в движущейся оболочке Н I. Если λs = λi то толщина оболочки остается неизменной, при λs > λi оболочка расширяется. Если скорость расширения оболочки относительно невелика - условие, которое часто встречается и которое мы будем считать выполненным, то
|
|
Из (6.29), считая, по-прежнему, заданной величину ρ1/ρ2 = R1(λs) - отношение заданных плотостей в зоне Н II и невозмущенной зоне Н I, находим уравнения зависимости от Xs для следующих величин: ρ'2 = ρ2R'2(λs) - плотности газа в оболочке сразу за фронтом ударной волны и ![]() - скорости движения газа (в неподвижной системе координат) также сразу за фронтом ударной волны.
Имеем
- скорости движения газа (в неподвижной системе координат) также сразу за фронтом ударной волны.
Имеем
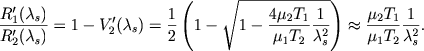
|
(6.52) |
Здесь T1 ≪ T2 и λs не малó по сравнению с единицей, иными словами, скорость оболочки больше скорости звука в Н I. Последнее равенство справедливо для сильной волны уплотнения (плотность газа в оболочке много больше, чем в области Н I).
Условия на ионизационном фронте также определяются (6.29), но уже с другими обозначениями параметров. Здесь неизвестны плотность на внутренней границе оболочки ![]() и соответствующая скорость газа
и соответствующая скорость газа ![]() . Теперь важно также учесть, что хотя T1 и мало по сравнению с T2, но скорость втекания газа в область фронта ионизационного разрыва
. Теперь важно также учесть, что хотя T1 и мало по сравнению с T2, но скорость втекания газа в область фронта ионизационного разрыва
![$$
v'_1(\lambda_i) = \lambda_i\sqrt{\frac{\Re T_2}{\mu_2}}[1 - V'_1(\lambda_i)]
$$](https://images.astronet.ru/pubd/2013/03/01/0001281314/tex/formula832.gif)
|
(6.53) |
также мала. Поэтому следует использовать полное соотношение (6.29):
![$$
\begin{array}{l} R'_1(\lambda_i) = \frac{1 - V_2(\lambda_i)}{1 - V'_1(\lambda_i)} = \frac{1}{2}\left(1 + \frac{\mu_2 T_1}{\mu_1 T_2} \frac{1}{\lambda_i^2 [1 - V_i(\lambda_i)]^2} + \right.\\ \left.+ \sqrt{\left(1 + \frac{\mu_2 T_1}{\mu_1 T_2} \frac{1}{\lambda_i^2 [1 - V'_1(\lambda_i)]^2}\right)^2} - \frac{4}{\lambda_i^2 [1 - V'_1(\lambda_i)]^2} \right).
\end{array}
$$](https://images.astronet.ru/pubd/2013/03/01/0001281314/tex/formula833.gif)
|
(6.54) |
Кроме того, согласно (6.48), величина λi[1 - V2(λi)] считается заданной условием (6.41). Итак, мы получили еще три соотношения для определения четырех величин R'1(λi), V'1(λi), V2(λi) и λi. Поскольку необходимо найти связь между λi и λs, нужны еще два условия. Очевидно, что они следуют из уравнений автомодельного движения газа в сжатой оболочке Н I.
Решения этих уравнений очень просты для плоских ионизационных фронтов (т. е. в случае (6.45)). Такое решение можно считать приближенно правильным, если относительная толщина оболочки мала. Тогда из (6.45) имеем
|
|
(6.55) |
Уравнения (6.55) и замыкают полную систему уравнений (6.48), (6.52), (6.54). Решение этой системы и в общем случае несложно, но его можно еще более упростить, рассмотрев случай, когда плотность газа в сжатой оболочке больше и плотности в H I и плотности в Н II. Тогда R'2(λs) = R'1(λi) ≫ 1 и соотношение (6.54) упрощается:
|
|
(6.56) |
Обозначая через А и α величины
|
|
(6.57) |
которые согласно условию считаются заданными, и полагая α ≪ 1, находим решение в безразмерных переменных:
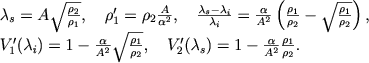
|
(6.58) |
Переходя к размерным переменным, имеем для скорости движения ударной волны в зоне Н I (по существу, для скорости движения всей оболочки):
|
|
(6.59) |
Плотность газа Н I внутри оболочки велика и определяется квадратом плотности потока ионизующих квантов:
|
|
(6.60) |
Относительная толщина оболочки соответственно мала:
|
|
(6.61) |
Эти простые результаты подтверждаются и численным расчетом более полной задачи.
Для сравнения приведем результаты Ласкера [24], полученные при численном интегрировании уравнений движения (рис. 23). Видны области сжатой оболочки с сильной ударной волной уплотнения, за которой следует ионизационная волна разрежения. Толщина сжатой оболочки в зоне Н I, действительно, относительно мала. Правда, наблюдаемые толщины сжатых оболочек обычно существенно больше и могут быть сравнимы с их радиусом. Возможно, что существенна роль магнитного поля [24], влияние которого, кстати, можно учесть также в рамках автомодельного метода.
Ионизационные фронты следует отличать от ионизующих ударных волн. У ионизационных фронтов меняется состояние ионизации благодаря прохождению через среду потока внешних квантов с энергией, большей порога ионизации, а у ионизующих ударных волн внутри фронта меняется состояние ионизации просто как следствие нагревания газа за фронтом ударной волны. Такие ударные волны большой интенсивности, распространяющиеся в неионизованном газе (например, в земной атмосфере), оставляют за собой область заметной ионизации. Хотя в астрофизике, вероятно, встречаются подобные ионизующие ударные волны, но особый интерес представляет исследование этих волн для прикладных задач геофизики и поэтому мы здесь эти волны рассматривать не будем.
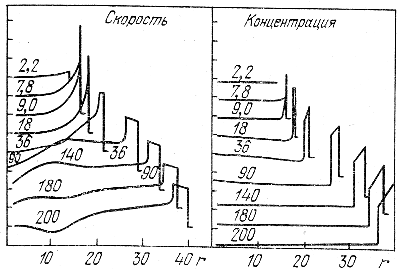
Рис. 23. Скорость (слева) и концентрация (справа) в случае движущегося ионизационного фронта, перед которым распространяется в зоне Н I ударная волна.
Различные кривые соответствуют разным моментам времени после начала расширения. Числа показывают это время в единицах 104 лет. Единица скорости - 3,2 км/сек, единица концентрации - 6,4 см-3 расстояние в пс.
Упомянем только о некоторых исследованиях движения ионизующих ударных волн в среде с магнитным полем. Обычно в астрофизике принимается условие "вмороженности" магнитного поля в вещество, когда электропроводность газа считается очень большой. Теория ударных волн с магнитным полем в условиях полной "вмороженности" магнитного поля в вещество излагалась применительно к астрофизическим задачам в книгах [4, 5].
Однако условие "вмороженности" магнитных силовых линий может нарушаться в области ионизационных разрывов и ионизующих ударных волн. В частности, если считать, что газ полностью нейтрален перед фронтом ионизующей ударной волны и сильно ионизован за ее фронтом, то на фронте такой ударной волны имеет место скачок электропроводности от нуля до очень большой величины. Следовательно, на фронте такой волны меняется условие "вмороженности" - от ее полного отсутствия до почти полной "приклеенности" магнитных силовых линий к движению вещества.
Такие ионизующие ударные волны со скачком электропроводности были рассмотрены в ряде работ А. А. Бармина, А. Г. Куликовского, Г. А. Любимова (см. [25, 26]). Основное внимание уделялось исследованию устойчивости подобных волн. В среде с магнитным полем есть большое число различных волн и поэтому следует учитывать возможность распада разрыва на любые комбинации линейных волн. В работе [26] рассматривалась и автомодельная задача о движении ионизующей ударной волны в параллельном фронту магнитном поле под действием поршня, движущегося с постоянной скоростью.
В астрофизических ионизационных разрывах тоже есть скачки электропроводности, но роль этих скачков не так велика. Дело в том, что даже в области неионизованного водорода есть заметная концентрация электронов от ионизации других элементов, и поэтому электропроводность достаточно велика и перед ионизационным фронтом. "Вмороженность" магнитных силовых линий имеет место как перед ионизационным фронтом, так и за ним. Кроме того, в реальных ионизационных разрывах в межзвездном пространстве имеет место не сжатие, а разрежение вещества, и, следовательно, не усиление, а, наоборот, ослабление магнитного поля. Конечно, полная теория ионизационных разрывов должна учитывать роль магнитного поля, но пока это еще не сделано.
Кроме ионизующих ударных волн и ионизационных разрывов возможны и рекомбинационные ударные волны и разрывы. Здесь движущей силой является энергия, выделяющаяся при рекомбинации газа. Такие ударные волны аналогичны волнам горения, хорошо известным в газодинамике. Свойства рекомбинационных разрывов в астрофизике изучались, например, в работе [27]. Но и ионизационные фронты по своим свойствам несколько напоминают волны горения, поскольку и здесь движущей силой является выделение энергии внутри фронта волны.
<< § 6.1 Уравнения автомодельного движения космического газа | Оглавление | § 6.3 Автомодельные движения в звездах и протозвездах >>