3.1 Поле Lc-излучения
После работы Milne [6] общепринятой является следующая модель планетарной туманности (и любой другой небулярной оболочки, окружающей звезду). Планетарная туманность представляет собой сферическую оболочку, толщина которой мала по сравнению с ее расстоянием от центра звезды. Вследствие этого оболочка может считаться состоящей из плоско-параллельных слоев, а коэффициент дилюции в оболочке - постоянным.
Пусть χ1c средний атомный коэффициент поглощения за границей серии Лаймана и τ - соответствующая оптическая глубина, отсчитанная от внутренней границы оболочки. Пусть далее πS1c - полное количество Lc-квантов, падающих от звезды на 1 см2 внутренней границы оболочки и K1c(τ1θ) - число квантов диффузного Lc-излучения, проходящих на глубине τ под углом θ к внешней нормали в единичном телесном угле через единичную площадку, перпендикулярную к лучам.
Так как число ионизации, происходящих из основного состояния, должно равняться числу захватов на все уровни, то мы получаем
|
|
(1) |
Обозначая через p долю захватов на первый уровень и вводя величину C1c, определенную соотношением
|
|
(2) |
Вместо (1) находим
|
|
(3) |
С другой стороны, величины C1c и K1c связаны друг с другом обычным уравнением переноса излучения
|
|
(4) |
Кроме того, имеют место следующие граничные условия:
|
|
(5) |
(условие на внутренней границе учитывает диффузное излучение, идущее с противоположной стороны туманности).
Таким образом задача об определении степени ионизации в туманности сводится к решению уравнений (3) и (4) при граничных условиях (5).
Из этих уравнений получается следующее интегральное уравнение для определения величины C1c(τ):
![$$
C_{1c}(\tau) = \frac{p}{2}\int\limits_0^{\tau_1} [Ei|\tau-\tau'| + Ei(\tau+\tau')]C_{1c}(\tau') d\tau' + p\frac{S_{1c}}{4}e^{-\tau} .
$$](https://images.astronet.ru/pubd/2011/06/28/0001252608/tex/formula5.gif)
|
(6) |
При τ = ∞ и на больших оптических глубинах вместо уравнения (6) получаем
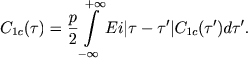
|
(7) |
Это уравнение имеет точное решение
|
|
(8) |
где k - корень уравнения
|
|
(9) |
а А - произвольная постоянная. Мы будем рассматривать функцию (8) как приближенное решение уравнения (6) и найдем постоянную А из того условия, чтобы уравнение (6) удовлетворялось точно в среднем. Тогда для А получаем
|
|
(10) |
Величина р является функцией от электронной температуры. Для планетарных туманностей можно, принять р = 1/2. Тогда из уравнения (9) находим k = 0,96. Мы видим, что найденное нами выражение для функции C1c(τ) сравнительно мало отличается от выражения, получающегося при учете только прямого излучения, идущего от звезды. Вследствие этого мы можем считать, что степень ионизации в туманности меняется по закону
|
|
(11) |
Следует отметить два обстоятельсва:
- При решении уравнений (3) и (4) приближенными методами для k получаем: k = 2(1-p)½ (методам Шварцшильда-Шустера) и k = (3(1-p))½ (методом Эддингтона). Различие между этими значениями k и тем значением, которое получается из уравнения (9), для многих вопросов, несомненно, существенно. Однако для планетарных туманностей, из-за большой роли прямого излучения, приближенные методы не приводят к серьезным ошибкам.
-
Выше весь лаймановский континуум мы заменили одним уровнем, приняв некоторый средний коэффициент поглощения. Более точная трактовка вопроса была дана Menzel с сотрудниками [4], составившими уравнение лучевого равновесия для каждого интервала частот (при этом были учтены не только фотоионизации и захваты, но и столкновения: электронов друг с другом и free-free transitions). Легко видеть, однако, что в этом нет необходимости, так как энергия, излучаемая элементарным объемом туманности за границей серии Лаймана, является известной функцией от частоты
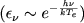 . Поэтому и при более точном рассмотрении вопроса мы снова приходим к интегральному уравнению типа (6) (с несколько более сложным ядром) для одной неизвеcтной функции, зависящей только от τ .
. Поэтому и при более точном рассмотрении вопроса мы снова приходим к интегральному уравнению типа (6) (с несколько более сложным ядром) для одной неизвеcтной функции, зависящей только от τ .
<< Глава III. Газовые туманности | Оглавление | 3.2 Поле Lα-излучения >>
|
Публикации с ключевыми словами:
оболочки звезд - перенос излучения
Публикации со словами: оболочки звезд - перенос излучения | |
|
См. также:
| |