3.2 Поле Lα-излучения
При рассмотрении поля Lc-излучения для нас не имело значения, движется оболочка или нет (поскольку скорости движения оболочки мала по сравнению со скоростью света). Теперь же мы допустим, что оболочка движется (скажем, расширяется) и притом с градиентом скорости. Для простоты предположим, что ![]() .
.
Так же как и раньше, мы будем считать, что коэффициент поглощения в линии является постоянным в интервале Δν12 и равен нулю вне этого интервала. При наличии градиента скорости некоторая часть Lα-квантов, приходящих в данное место оболочки (частоты которых не попадают в указанный интервал), не будут поглощаться в этом месте. Вследствие этого интегральное уравнение, определяющее плотность Lα-излучения, будет иметь совсем другой вид, чем при отсутствии градиента скорости.
Переходя к составлению этого уравнения, условимся в том, что, говоря о плотности Lα-излучения, мы будем иметь в виду только те Lα-кванты из находящихся в данном объеме, которые могут быть поглощены в этом объеме.
Будем исходить из условия стационарности для второго уровня водородного атома:
|
|
(12) |
Так как оболочка предполагается прозрачной для излучения в линиях субординатных серий, то мы имеем
|
|
(13) |
Подставляя (13) в (12) и учитывая результаты предыдущего параграфа, получаем
|
|
(14) |
Положим
|
|
(15) |
|
|
(16) |
где χ12 - средний атомный коэффициент поглощения в линии Lα. Тогда вместо (13) находим
|
|
(17) |
В рассматриваемом случае, т.е. при наличии градиента скорости в оболочке, вторым уравнением, связывающим величины С12 и К12, уже не может служить обычное уравнение переноса излучения. Вместо этого уравнения, с помощью тех же соображений, которые были изложены в главе I, мы получаем следующее более сложное интегральное соотношение:
![$$
K_{12}(t,\theta) = \int\limits_0^t C_{12}(t')e^{-(t-t')\sec\theta} [1-\beta(t-t')\cos\theta]\sec\theta dt' \qquad (\theta<\frac{\pi}{2}) ,
$$](https://images.astronet.ru/pubd/2011/06/28/0001252608/tex/formula96.gif)
|
(18) |
где через t обозначена оптическая глубина в линии Lα, а величина β имеет прежнее значение, т.е.
|
|
(19) |
Мы пренебрегли здесь излучением в линий Lα, падающим на внутреннюю границу оболочки, как от звезды, так и от противоположных частей оболочки (последнее означает, что скорость расширения внутренней границы мы считаем достаточно большой по сравнению со средней термической скоростью атомов).
Подставляя соотношение (18) (и аналогичное соотношение для углов θ, больших π/2 в уравнение (17), мы получаем следующее интегральное уравнение, определяющее величину С12:
![$$
C_{12}(t) = \frac{1}{2}\int\limits_0^{t_1} C_{12}(t')[Ei|t-t'|-\beta Ei_2|t'-t|\cdot|t'-t|]dt'+q\psi(\tau) ,
$$](https://images.astronet.ru/pubd/2011/06/28/0001252608/tex/formula98.gif)
|
(20) |
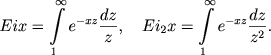
|
(21) |
Так как мы считаем, что оптическая толщина τ туманности за границей серии Лаймана больше единицы, то оптическая толщина t1 в линии Lα должна быть больше 104. Поэтому для средних частей туманности пределы интегрирования в (20) можно заменить на бесконечные. Легко убедиться, что решение полученного таким образом уравнения имеет вид
|
|
(22) |
|
|
(23) |
В форме (22) мы будем искать решение уравнения (20), определяя постоянные А и В из условий вблизи границ. Подставляя (22) в (20) и считая, что t мало, получаем
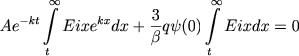
|
(24) |
Заставляя это уравнение выполняться точно в среднем, находим
|
|
(25) |
Совершенно аналогично получаем выражения для B
|
|
(26) |
Так как величина β мала, то из (23) приближенно следует
|
|
(27) |
Поэтому окончательно решение уравнеия (20) можно записать в виде
|
|
(28) |
Кроме величины C12(t), нас интересует также поток Lα-квантов, определяющий световое давление в туманности. Пренебрегая членом с множителем β, для этого потока имеем
![$$
F(t) = 2\pi\left[\int\limits_0^t E_{i_2} (t-t')C_{12}(t')dt' - \int\limits_t^{t'} E_{i_2} (t'-t)C_{12}(t')dt'\right].
$$](https://images.astronet.ru/pubd/2011/06/28/0001252608/tex/formula107.gif)
|
(29) |
Для средних частей туманности эта формула дает
|
|
(30) |
На границах же поток равен
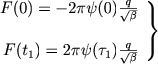
|
(31) |
Рассмотрим теперь для сравнения туманность, расширяющуюся без градиента скорости. В этом случае в уравнении (20) надо положить β=0. Тогда для средних частей туманности решение уравнения (20) будет иметь вид
|
|
(32) |
Для потока Lα-излучения на внутренней границе туманности без всяких вычислений получаем
|
|
(33) |
(так как при отсутствии градиента скорости поток Lα-квантов на внутренней границе должен быть равен потоку Lc-квантов, идущих от центральной звезды).
Сравнивая формулы (32) и (33) соответственно с формулами (28) и (31), мы видим, что появление градиента скорости в туманности чрезвычайно резко понижает плотность и поток Lα-излучения. Допустим, например, что скорости ![]() одного порядка. Тогда первая из формул (31) дает для потока Lα-излучения на внутренней границе туманности значение в несколько сот раз меньшее, чем формула (33). А для плотности Lα-излучения в средних частях туманности по формуле (28) получается значение в несколько десятков тысяч раз меньше, чем по формуле (32).
одного порядка. Тогда первая из формул (31) дает для потока Lα-излучения на внутренней границе туманности значение в несколько сот раз меньшее, чем формула (33). А для плотности Lα-излучения в средних частях туманности по формуле (28) получается значение в несколько десятков тысяч раз меньше, чем по формуле (32).
Как уже указывалось, поле Lα-излучения в туманности, движущейся без градиента скорости, впервые было рассмотрено В. А. Амбарцумяном. При этом была выяснена большая роль светового давления, вызванного Lα-излучением. Подсчеты показали, что на внутренней границе туманности световое давление примерно в 1000 раз превосходит силу лритяжения центральной звезды. Этот вывод являлся важным по двум причинам: во-первых, потому, что он открывал перспективы построения динамики туманности при учете только одной силы - светового давления, обусловленного Lα-излучением; и, во-вторых, потому, что он указывал на сильное торможение внутренних частей туманности и тем самым подкреплял гипотезу о происхождении планетарных туманностей из оболочек сверхновых звезд. (Как известно, оболочки сверхновых звезд выбрасываются с огромными скоростями порядка нескольких тысяч километров в секунду, а планетарные туманности расширяются со скоростями порядка нескольких десятков километров в секунду; объяснение этого различия одним только гравитационным торможением является неправдоподобным).
Однако в действительности необходимо считать, что туманность движется с градиентом скорости (ибо если бы в некоторый момент времени туманность и двигалась с постоянной для всех слоев скоростью, то постепенно, благодаря световому давлению, все равно создалась бы разность скоростей расширения). Но появление градиента скорости, как показано выше, резко уменьшает поток Lα-излучения. Поэтому мы приходим к выводу, что световое давление, вызванное Lα-излучением, не играет в туманности той большой роли, которая ему раньше приписывалась.
Следует отметить, что задача, решенная нами в этом параграфе, была раньше рассмотрена Zanstra [5], Однако метод, принятый Zanstra, отличается от нашего. Zanstra, рассматривая туманность, ограниченную параллельными плоскостями, учитывал только ту составляющую скорости атома, которая перпендикулярна к этим границам. Приближенно он считал, что если эта составляющая одинакова для атомов, то они могут поглощать излучение друг от друга; если различны, то не могут.
Ясно, что при таком предположении быстро летящие атомы оказываются способными поглощать (а значит и излучать) лишь очень небольшое количество энергии, так как они лишаются возможности поглощать излучение, идущее с боков. Поэтому контур линии излучения, образованной элементарным объемом, получается не прямоугольный, а параболический. Эта разница оказывается очень существенной, так как во втором случае доля непоглощаемой энергии будет значительно меньше, чем в первом. Вследствие этого плотность и поток Lα-излучения, полученные методом Zanstra, должны резко отличаться от наших.
Так это и есть на самом деле. Взяв занстровское значение потока Lα-излучения из книги В. А. Амбарцумяна [7]
|
|
(34) |
и сравнив его с нашим значением [см. формулу (30)], мы видим, что разница между решениями огромна. Если, например, принять, что скорости ![]() одного порядка, то получается, что занстровский поток, будет примерно в 10000 раз больше, чем наш. Поэтому надо признать, что решение Zanstra является просто неверным.*
одного порядка, то получается, что занстровский поток, будет примерно в 10000 раз больше, чем наш. Поэтому надо признать, что решение Zanstra является просто неверным.*
Сущность ошибки Zanstra состоит в том, что он не учитывает изменения частоты световых квантов, происходящего при элементарном акте рассеяния, вследствие молекулярного эффекта Допплера, т. е. считает, что рассеяние света является когерентным. Для движущейся среды, для которой эффект Доплера вообще играет огромную роль, эта ошибка бросается в глаза. Однако некогерентность рассеяния света имеет большое значение и для неподвижных атмосфер. Ввиду важности этого вопроса мы в дальнейшем посвятим ему отдельное исследование.
* То же самое надо сказать и о другой работе Zanstra [8], в которой дано применение результатов его первой работы к динамике газовых туманностей.
<< 3.1 Поле Lc-излучения | Оглавление | 3.3 Температуры туманностей и температуры ядер >>
|
Публикации с ключевыми словами:
оболочки звезд - перенос излучения
Публикации со словами: оболочки звезд - перенос излучения | |
|
См. также:
| |