1.2 Степень возбуждения и ионизации
Для решения системы (9) необходимо знать значение функций Ci и Bicρic* для данного атома. Для атома водорода эти функции имеют вид (см. цитированную работу Cillie):
|
|
(13) |
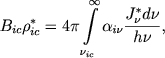
|
(14) |
|
|
(15) |
где m и e - масса и заряд электрона; h - постоянная Планка и k - постоянная Больцмана.
Легко видеть, что если система (9) решена для водорода, то полученные результаты могут быть использованы для ионизованного гелия. В самом деле, мы имеем: спектральные термы He+ в 4 раза больше термов Н, коэффициенты спонтанных переходов для He+ в 16 раз больше, чем для Н, а статистические веса состояний совпадают (см. работу В. А. Амбарцумяна [2]). Поэтому из рассмотрения системы (9) мы приходим к следующему выводу: числа ![]() для ионизованного гелия будут в 8 раз меньше соответствующих чисел для водорода, если принять температуру в 4 раза большую.
для ионизованного гелия будут в 8 раз меньше соответствующих чисел для водорода, если принять температуру в 4 раза большую.
Систему (9) мы решили численно для водородного атома. При этом мы считали, что температура среды совпадает с температурой звезды. Если эти температуры различны, то в уравнениях (9) величины Bicρic* будут функциями от T∗, а величины Ci - функциями от Te. Однако из рассмотренных нами случаев легко сделать переход к другим случаям. Это связано с тем, что относительные значения величин Ci очень мало меняются с изменением Te. Поэтому и относительные значения величин ni будут также слабо зависеть от Te. Так, например, при Te=10000°; все величины ni будут приблизительно в 2 раза больше, чем при Te=20000°; .
Мы рассмотрели следующие случаи: T = 20000°; , x = 0; 0,01; 0,1; 1,0; T=50000°; ; х = 0; 0,1; 1,0; 10. Результаты вычислений приведены в таблицах I, II и III.
Таблица I
![]()
| T\x | 0 | 0.01 | 0.1 | 1.0 | 10 | ∞ |
| 20000 | 0.027 | 0.022 | 0.015 | 0.014 | - | 0.014 |
| 50000 | 11.8 | - | 9,4 | 7.3 | 6.8 | 6.8 |
Таблица II
![]() (T=20000o)
(T=20000o)
| k\x | 0 | 0.01 | 0.1 | 1.0 |
| 2 | 1.06 | 0.97 | 0.29 | 0.036 |
| 3 | 0.64 | 0.33 | 0.030 | 0.00056 |
| 4 | 0.60 | 0.20 | 0.0085 | 0.000058 |
| 5 | 0.61 | 0.16 | 0.0037 | 0.000012 |
| 6 | 0.65 | 0.14 | 0.0021 | 0.000004 |
Таблица III
![]() (T=50000o)
(T=50000o)
| k\x | 0 | 0.1 | 1.0 | 10 |
| 2 | 0.30 | 0.18 | 0.046 | 0.0067 |
| 3 | 0.26 | 0.13 | 0.019 | 0.00095 |
| 4 | 0.28 | 0.12 | 0.012 | 0.00030 |
| 5 | 0.31 | 0.11 | 0.009 | 0.00015 |
| 6 | 0.34 | 0.10 | 0.007 | 0.00010 |
Из табл. I видно, что степень ионизации слабо зависит от параметра х. Можно считать, что при любых значениях х степень ионизации определяется обычной ионизационной формулой (с множителем W в правой части).*
Напротив, степень возбуждения, мало отличающаяся от больцмановской, при x = 0, чрезвычайно быстро убывает с возрастанием величины х. Это значит, что для нахождения степени возбуждения в движущихся оболочках звезд ни в коем случае нельзя пользоваться формулой Больцмана. Убывание степени возбуждения с увеличением величины х (особенно быстрое для высоких уровней) приводит к тому, что при достаточно больших значениях х среда становится прозрачной для излучения в линиях данной серии. К таким случаям результаты, полученные в этом параграфе, неприменимы. Эти случаи подробно рассматриваются в § 4.
* Это связано с нашим предположением о малости оптической толщины среды за границей основной серии. Если эта оптическая среда велика, то, как будет показано в главе IV , изменение степени ионизации с оптической глубиной сильно зависит от параметра х.
<< 1.1 Основные уравнения | Оглавление | 1.3 Относительные интенсивности линий >>
|
Публикации с ключевыми словами:
оболочки звезд - перенос излучения
Публикации со словами: оболочки звезд - перенос излучения | |
|
См. также:
| |