4. Вещество при очень больших плотностях, нейтронизация, взаимодействие частиц
При очень больших плотностях в условиях сильною вырождения электронов
и нуклонов приближенно вещество можно считать холодным с ![]() [110].
[110].
а) Холодная нейтронизация вдоль состояний минимума энергии (СМЭ).
При плотностях
![]() вещество в СМЭ состоит
из
вещество в СМЭ состоит
из ![]() , ядра которого максимально стабильны6. Когда
, ядра которого максимально стабильны6. Когда
![]() из (2.21) достигает значения
из (2.21) достигает значения
![]() при
при
|
|
(4.1) |
При нулевой температуре состояние термодинамического равновесия соответствует
минимуму полной энергии ![]() как функции
как функции ![]() и
и ![]() при данном числе нуклонов в единице объема. С ростом плотности равновесие
смещается в сторону все более переобогащенных нейтронами ядер. При
при данном числе нуклонов в единице объема. С ростом плотности равновесие
смещается в сторону все более переобогащенных нейтронами ядер. При
![]() энергия связи последнего нейтрона в ядре
энергия связи последнего нейтрона в ядре
![]() близка к нулю и в равновесии появляются свободные нейтроны.
В равновесии плотность, при которой начинают отщепляться нейтроны,
равна
близка к нулю и в равновесии появляются свободные нейтроны.
В равновесии плотность, при которой начинают отщепляться нейтроны,
равна
![]() [267].
[267].
В отсутствие свободных нейтронов при
![]() для энергии
единицы объема с учетом энергии покоя имеем [267]
для энергии
единицы объема с учетом энергии покоя имеем [267]
| (4.2) |
| (4.3) |
| (4.4) |
| (4.5) |
| Ядро |
|
Z/A |
|
|
|
| 8.7905 | 0.4643 | 8.1 (6) | 0.95 | 2.9 | |
| 8.7947 | 0.4516 | 2.7 (8) | 2.6 | 3.1 | |
| 8.7777 | 0.4375 | 1.2 (9) | 4.2 | 7.9 | |
| 8.6797 | 0.4048 | 8.2 (9) | 7.7 | 3.5 | |
| 8.5964 | 0.3902 | 2.2 (10) | 10.6 | 3.8 | |
| 8.4675 | 0.3750 | 4.8 (10) | 13.6 | 4.1 | |
| 8.2873 | 0.3590 | 1.6 (11) | 20.0 | 4.6 | |
| 7.9967 | 0.3421 | 1.8 (11) | 20.2 | 2.2 | |
| 7.8577 | 0.3387 | 1.9 (11) | 20.5 | 3.1 | |
| 7.6705 | 0.3279 | 2.7 (11) | 22.9 | 3.3 | |
| 7.4522 | 0.3166 | 3.7 (11) | 25.2 | 3.5 | |
| 7.2002 | 0.3051 | (4.3 (11)) | (26.2) | ... | |
| Здесь
|
|||||
В таблице 7 даны результаты расчета термодинамических функций при
равновесной нейтронизации. При
![]() ,
когда энергия взаимодейстция
,
когда энергия взаимодейстция ![]() становится порядка кинетической
энергии электронов, значения в табл. 7 взяты из работы [201].
становится порядка кинетической
энергии электронов, значения в табл. 7 взяты из работы [201].
|
|
|
|
Z | A | Г |
| 7.86 | 4.73 (24) | 26 | 56 | ... | |
| 7.90 | 1.01 (10) | 4.76 (24) | 26 | 56 | ... |
| 8.15 | 1.01 (11) | 4.91 (24) | 26 | 56 | ... |
| 11.6 | 1.21 (12) | 6.99 (24) | 26 | 56 | ... |
| 16.4 | 1.40 (13) | 9.90 (24) | 26 | 56 | ... |
| 45.1 | 1.70 (14) | 2.72 (25) | 26 | 56 | ... |
| 212 | 5.82 (15) | 1.27 (26) | 26 | 56 | ... |
| 1150 | 1.90 (17) | 6.93 (26) | 26 | 56 | ... |
| 1.044 (4) | 9.744 (18) | 6.295 (27) | 26 | 56 | 1.796 |
| 2.622 (4) | 4.968 (19) | 1.581 (28) | 26 | 56 | 1.744 |
| 6.587 (4) | 2.431 (20) | 3.972 (28) | 26 | 56 | 1.706 |
| 1.654 (5) | 1.151 (21) | 9.976 (28) | 26 | 56 | 1.670 |
| 4.156 (5) | 5.266 (21) | 2.506 (29) | 26 | 56 | 1.631 |
| 1.044 (6) | 2.318 (22) | 6.294 (29) | 26 | 56 | 1.586 |
| 2.622 (6) | 9.755 (22) | 1.581 (30) | 26 | 56 | 1.534 |
| 6.588 (6) | 3.911 (23) | 3.972 (30) | 26 | 56 | 1.482 |
| 8.293 (6) | 5.259 (23) | 5.000 (30) | 28 | 62 | 1.471 |
| 1.655 (7) | 1.435 (24) | 9.976 (30) | 28 | 62 | 1.437 |
| 3.302 (7) | 3.833 (24) | 1.990 (31) | 28 | 62 | 1.408 |
| 6.589 (7) | 1.006 (25) | 3.972 (31) | 28 | 62 | 1.386 |
| 1.315 (8) | 2.604 (25) | 7.924 (31) | 28 | 62 | 1.369 |
| 2.624 (8) | 6.676 (25) | 1.581 (32) | 28 | 62 | 1.357 |
| 3.304 (8) | 8.738 (25) | 1.990 (32) | 28 | 64 | 1.355 |
| 5.237 (8) | 1.629 (26) | 3.155 (32) | 28 | 64 | 1.350 |
| 8.301 (8) | 3.029 (26) | 5.000 (32) | 28 | 64 | 1.346 |
| 1.045 (9) | 4.129 (26) | 6.294 (32) | 28 | 64 | 1.344 |
| 1.316 (9) | 5.036 (26) | 7.924 (32) | 34 | 84 | 1.343 |
| 1.657 (9) | 6.860 (26) | 9.976 (32) | 34 | 84 | 1.342 |
| 2.626 (9) | 1.272 (27) | 1.581 (33) | 34 | 84 | 1.340 |
| 4.164 (9) | 2.356 (27) | 2.506 (33) | 34 | 84 | 1.338 |
| 6.601 (9) | 4.362 (27) | 3.972 (33) | 34 | 84 | 1.337 |
| 8.312 (9) | 5.662 (27) | 5.000 (33) | 32 | 82 | 1.336 |
| 1.046 (10) | 7.702 (27) | 6.294 (33) | 32 | 82 | 1.336 |
| 1.318 (10) | 1.048 (28) | 7.924 (33) | 32 | 82 | 1.336 |
| 1.659 (10) | 1.425 (28) | 9.976 (33) | 32 | 82 | 1.335 |
| 2.090 (10) | 1.938 (28) | 1.256 (34) | 32 | 82 | 1.335 |
| 2.631 (10) | 2.503 (28) | 1.581 (34) | 30 | 80 | 1.335 |
| 3.313 (10) | 3.404 (28) | 1.990 (34) | 30 | 80 | 1.335 |
| 4.172 (10) | 4.628 (28) | 2.506 (34) | 30 | 80 | 1.334 |
| 5.254 (10) | 5.949 (28) | 3.155 (34) | 28 | 78 | 1.334 |
| 6.617 (10) | 8.089 (28) | 3.972 (34) | 28 | 78 | 1.334 |
| 8.332 (10) | 1.100 (29) | 5.000 (34) | 28 | 78 | 1.334 |
| 1.049 (11) | 1.495 (29) | 6.294 (34) | 28 | 78 | 1.334 |
| 1.322 (11) | 2.033 (29) | 7.924 (34) | 28 | 78 | 1.334 |
| 1.664 (11) | 2.597 (29) | 9.976 (34) | 26 | 76 | 1.334 |
| 1.844 (11) | 2.892 (29) | 1.105 (35) | 42 | 124 | 1.334 |
| 2.096 (11) | 3.290 (29) | 1.256 (35) | 40 | 122 | 1.334 |
| 2.640 (11) | 4.473 (29) | 1.581 (35) | 40 | 122 | 1.334 |
| 3.325 (11) | 5.816 (29) | 1.990 (35) | 38 | 120 | 1.334 |
| 4.188 (11) | 7.538 (29) | 2.506 (35) | 36 | 118 | 1.334 |
| 4.299 (11) | 7.805 (29) | 2.572 (35) | 36 | 118 | 1.334 |
б) Появление свободных нуклонов. СМЭ при субъядерных плотностях с учетом взаимодействия нуклонов.
При
![]() все связанные состояния нейтронов в ядрах
оказываются заполненными и дальнейший рост плотности приводит к появлению
свободных нейтронов. После различных попыток расчета уравнения состояния
в этой области (см. обзор [266]), корректный подход к решению
проблемы был развит в работе [265]. Этот подход основан на следующих
принципах.
все связанные состояния нейтронов в ядрах
оказываются заполненными и дальнейший рост плотности приводит к появлению
свободных нейтронов. После различных попыток расчета уравнения состояния
в этой области (см. обзор [266]), корректный подход к решению
проблемы был развит в работе [265]. Этот подход основан на следующих
принципах.
- Единое описание энергии взаимодействия нуклонов как внутри, так
и вне ядер.
- Использование выражения для поверхностной энергии ядер, которое
учитывает наличие окружающих нейтронов и обращается в нуль при идентичности
вещества внутри и снаружи.
- Учет энергии кулоновского взаимодействия электронов и ядер решетки, а также протонов внутри ядра.
Если ![]() и
и ![]() - концентрации ядер и свободных
нейтронов в пространстве вне ядер,
- концентрации ядер и свободных
нейтронов в пространстве вне ядер, ![]() - объем ядра, а
то выражение для полной энергии единицы объема
- объем ядра, а
то выражение для полной энергии единицы объема ![]() запишется
в виде
запишется
в виде
| (4.6) |
Для нахождения равновесного состава и уравнения состояния необходимо
минимизировать ![]() относительно аргументов при постоянной
концентрации нуклонов
относительно аргументов при постоянной
концентрации нуклонов ![]() :
:
| (4.7) |
Входящие в (4.6) кулоновская энергия решетки ![]() и энергия
холодных электронов определены в (4.4) и (2.22), (2.23) соответственно.
Энергия ядра, представляемого в виде жидкой капли, записывается в
виде
и энергия
холодных электронов определены в (4.4) и (2.22), (2.23) соответственно.
Энергия ядра, представляемого в виде жидкой капли, записывается в
виде
![\begin{displaymath}
\eqalign{ W_{A,Z}\left( A,Z,V_{A,Z},n_{n}\right) =& \left[ \left( 1-x\right) m_{n}c^{2}+xm_{p}c^{2}+W\left( k,x\right) \right] A+ \cr & +W_{coul}\left( A,Z,V_{A,Z},n_{n}\right) +W_{surf}\left( A,Z,V_{A,Z},n_{n}\right), \quad
x=\frac{Z}{A}, \cr }
\end{displaymath}](https://images.astronet.ru/pubd/2006/01/25/0001211125/tex/formula833.gif) |
(4.8) |
| (4.9) |
Функция
![]() , входящая в (4.8), (4.9), а также
, входящая в (4.8), (4.9), а также
![]() и
и ![]() , входящие в (4.8), вычислены в [266].
Поверхностная энергия в [265] оценивалась довольно грубо из соображений
размерности. Более точные выражения для
, входящие в (4.8), вычислены в [266].
Поверхностная энергия в [265] оценивалась довольно грубо из соображений
размерности. Более точные выражения для ![]() были найдены
в работах [313] методом Томаса-Ферми, [256] вариационным методом
и [504, 548] методом Хартри-Фока. Величина -
были найдены
в работах [313] методом Томаса-Ферми, [256] вариационным методом
и [504, 548] методом Хартри-Фока. Величина -
![]() по физическому смыслу есть энергия связи ядра
по физическому смыслу есть энергия связи ядра
![]() с учетом окружающей плотности нейтронов, которая для нормальных ядер
в вакууме аппроксимируется формулой Вейцзеккера (4.3). Минимизация
величины
с учетом окружающей плотности нейтронов, которая для нормальных ядер
в вакууме аппроксимируется формулой Вейцзеккера (4.3). Минимизация
величины ![]() относительно своих аргументов при постоянстве
относительно своих аргументов при постоянстве
![]() из (4.7) сводится к четырем уравнениям, определяющим
равновесие по следующим процессам: 1) сжатие и расширение ядра давлением
внешних нейтронов, 2) обмен нейтронами между ядром и нейтронным газом,
3) превращение нейтронов и протонов друг в друга внутри ядра, 4) выделение
ядра, минимизирующего полную энергию. Решение этих четырех уравнений
определяет свойства равновесного вещества, состоящего из ядер и свободных
нейтронов. В табл.8 из [265] приведены результаты расчетов. С
увеличением плотности происходит рост массы и объема ядер, пока они
не касаются друг друга при
из (4.7) сводится к четырем уравнениям, определяющим
равновесие по следующим процессам: 1) сжатие и расширение ядра давлением
внешних нейтронов, 2) обмен нейтронами между ядром и нейтронным газом,
3) превращение нейтронов и протонов друг в друга внутри ядра, 4) выделение
ядра, минимизирующего полную энергию. Решение этих четырех уравнений
определяет свойства равновесного вещества, состоящего из ядер и свободных
нейтронов. В табл.8 из [265] приведены результаты расчетов. С
увеличением плотности происходит рост массы и объема ядер, пока они
не касаются друг друга при
![]() .
В [265] предполагается, что при плотности
.
В [265] предполагается, что при плотности ![]() происходит
фазовый переход первого рода к однородной ядерной материи.
происходит
фазовый переход первого рода к однородной ядерной материи.
|
|
|
|
Z | A | Г |
| 4.460(11) | 7.890(29) | 2.,670(35) | 40 | 126 | 0.40 |
| 5.228(11) | 8.352(29) | 3.126(35) | 40 | 128 | 0.36 |
| 6.610(11) | 9.098(29) | 3.951(35) | 40 | 130 | 0.40 |
| 7.964(11) | 9.831(29) | 4.759(35) | 41 | 132 | 0.46 |
| 9.728(11) | 1.083(30) | 5.812(35) | 41 | 135 | 0.54 |
| 1.196(12) | 1.218(30) | 7.143(35) | 42 | 137 | 0.63 |
| 1.471(12) | 1.399(30) | 8.786(35) | 42 | 140 | 0.73 |
| 1.805(12) | 1.638(30) | 1.077(36) | 43 | 142 | 0.83 |
| 2.202(12) | 1.950(30) | 1.314(36) | 43 | 146 | 0.93 |
| 2.930(12) | 2.592(30) | 1.748(36) | 44 | 151 | 1.06 |
| 3.833(12) | 3.506(30) | 2.287(36) | 45 | 156 | 1.17 |
| 4.933(12) | 4.771(30) | 2.942(36) | 46 | 163 | 1.25 |
| 6.248(12) | 6.481(30) | 3.726(36) | 48 | 170 | 1.31 |
| 7.801(12) | 8.748(30) | 4.650(36) | 49 | 178 | 1.36 |
| 9.611(12) | 1.170(31) | 5.728(36) | 50 | 186 | 1.39 |
| 1.246(13) | 1.695(31) | 7.424(36) | 52 | 200 | 1.43 |
| 1.496(13) | 2.209(31) | 8.907(36) | 54 | 211 | 1.44 |
| 1.778(13) | 2.848(31) | 1.059(37) | 56 | 223 | 1.46 |
| 2.210(13) | 3.931(31) | 1.315(37) | 58 | 241 | 1.47 |
| 2.988(13) | 6.178(31) | 1.777(37) | 63 | 275 | 1.49 |
| 3.767(13) | 8.774(31) | 2.239(37) | 67 | 311 | 1.51 |
| 5.081(13) | 1.386(32) | 3.017(37) | 74 | 375 | 1.53 |
| 6.193(13) | 1.882(32) | 3.675(37) | 79 | 435 | 1.54 |
| 7.732(13) | 2.662(32) | 4.585(37) | 88 | 529 | 1.56 |
| 9.826(13) | 3.897(32) | 5.821(37) | 100 | 683 | 1.60 |
| 1.262(14) | 5.861(32) | 7.468(37) | 117 | 947 | 1.65 |
| 1.586 (14) | 8.595 (32) | 9.371 (37) | 143 | 1390 | 1.70 |
| 2.004(14) | 1.286(33) | 1.182(38) | 201 | 2500 | 1.74 |
| 2.520(14) | 1.900(33) | 1.484(38) | ... | ... | 1.81 |
| 2.761(14) | 2.242(33) | 1.625(38) | ... | ... | 1.82 |
| 3.085(14) | 2.751(33) | 1.814(38) | ... | ... | 1.87 |
| 3.433(14) | 3.369(33) | 2.017(38) | ... | ... | 1.92 |
| 3.885(14) | 4.286(33) | 2.280(38) | ... | ... | 1.97 |
| 4.636(14) | 6.103(33) | 2.715(38) | ... | ... | 2.03 |
| 5.094(14) | 7.391(33) | 2.979(38) | ... | ... | 2.05 |
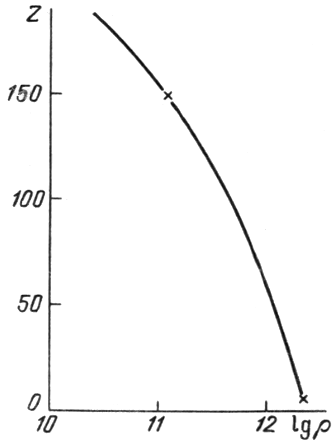
Уточнение формулы для поверхностной энергии сказалось только на изменении
заряда ядра
![]() , рост которого замедлился
по сравнению с [265]. На рис. 7 из [266] приведены результаты
расчета
, рост которого замедлился
по сравнению с [265]. На рис. 7 из [266] приведены результаты
расчета
![]() различными авторами. Уменьшение
величины
различными авторами. Уменьшение
величины ![]() при больших плотностях приводит к более плавному
изменению
при больших плотностях приводит к более плавному
изменению ![]() в процессе фазового перехода к однородной ядерной
материи. Несовпадение зависимостей
в процессе фазового перехода к однородной ядерной
материи. Несовпадение зависимостей
![]() у
авторов [256, 313, 504, 548] отражает как недостаток физических
знаний о законах взаимодействий между нуклонами, так и несовер шенство
существующих математических методов расчета.
у
авторов [256, 313, 504, 548] отражает как недостаток физических
знаний о законах взаимодействий между нуклонами, так и несовер шенство
существующих математических методов расчета.
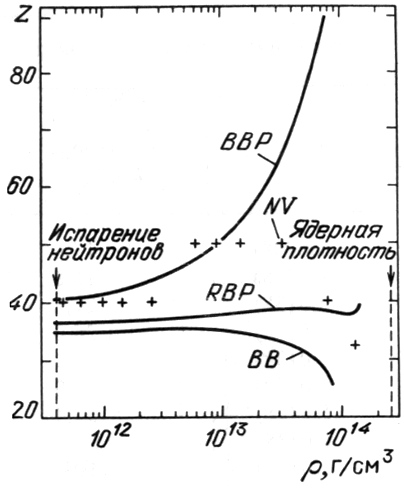 |
| Рис. 7.
Зависимость заряда |
в) Плотность, больше ядерной.
Однородная ядерная материя (ЯМ), появляющаяся в результате фазового
перехода, состоит из нейтронов с небольшой примесью протонов и электронов.
Пока плотность ЯМ не превышает ![]() (
(
![]() - плотность свободной ЯМ), для расчета уравнения состояния применим
метод Бракнера-Бете-Голдстоуна, основанный на теории возмущений [22].
При
- плотность свободной ЯМ), для расчета уравнения состояния применим
метод Бракнера-Бете-Голдстоуна, основанный на теории возмущений [22].
При
![]() расчеты ведутся с помощью вариационного
принципа, разработанного Пандарипанде [537]. При больших плотностях
учитывается рождение тяжелых гиперонов [9] и возможное рождение
расчеты ведутся с помощью вариационного
принципа, разработанного Пандарипанде [537]. При больших плотностях
учитывается рождение тяжелых гиперонов [9] и возможное рождение
![]() -мезонов (пионная конденсация [158]). Расчеты уравнения
состояния ядерной материи при
-мезонов (пионная конденсация [158]). Расчеты уравнения
состояния ядерной материи при
![]() выполнены
при различных допущениях в [275, 479]. В табл. 9 из [479]
приводится уравнение состояния для наиболее реалистического варианта
с параметрами потенциала взаимодействия, учитывающими экспериментальные
данные из ядерной физики высоких энергий, а также рождение гиперонов.
Возможное появление пионной конденсации слабо влияет на уравнение
состояния [275]. Следует иметь в виду, что с ростом плотности
все более возрастает неопределенность наших знаний о физике сильных
взаимодействий и менее точными становятся методы расчета. В связи
с этим даже в реалистическом варианте из табл. 9 погрешности могут
достигать ~ 50%.
выполнены
при различных допущениях в [275, 479]. В табл. 9 из [479]
приводится уравнение состояния для наиболее реалистического варианта
с параметрами потенциала взаимодействия, учитывающими экспериментальные
данные из ядерной физики высоких энергий, а также рождение гиперонов.
Возможное появление пионной конденсации слабо влияет на уравнение
состояния [275]. Следует иметь в виду, что с ростом плотности
все более возрастает неопределенность наших знаний о физике сильных
взаимодействий и менее точными становятся методы расчета. В связи
с этим даже в реалистическом варианте из табл. 9 погрешности могут
достигать ~ 50%.
Как отмечалось впервые Я.Б. Зельдовичем [103, 110], требование
принципа причинности о том, что скорость звука ![]() не
должна превышать скорость света
не
должна превышать скорость света ![]() , накладывает ограничение
на уравнение состояния
, накладывает ограничение
на уравнение состояния
![]() . Важность
этого ограничения связана с тем, что оно действует при сколь угодно
больших плотностях, где о свойствах ядерных взаимодействий известно
очень мало.
. Важность
этого ограничения связана с тем, что оно действует при сколь угодно
больших плотностях, где о свойствах ядерных взаимодействий известно
очень мало.
|
|
|
|
|
| 1.0 (38) | 12.6 | 1.70 (14) | 1.19 (33) |
| 1.5 (38) | 16.6 | 2.55 (14) | 2.93 (33) |
| 2.0 (38) | 21.2 | 3.42 (14) | 6.00 (33) |
| 2.5 (38) | 26.0 | 4.31 (14) | 1.09 (34) |
| 3.0 (38) | 32.2 | 5.21 (14) | 1.83 (34) |
| 4.0 (38) | 46.9 | 7.04 (14) | 4.09 (34) |
| 5.0 (38) | 64.4 | 8.95 (14) | 7.61 (34) |
| 6.0 (38) | 83.7 | 1.09 (15) | 1.26 (35) |
| 7.0 (38) | 109 | 1.31 (15) | 1.99 (35) |
| 8.0 (38) | 134 | 1.54 (15) | 2.85 (35) |
| 9.0 (38) | 160 | 1.76 (15) | 3.71 (35) |
| 1.0 (39) | 189 | 2.01 (15) | 4.02 (35) |
| 1.1 (39) | 215 | 2.26 (15) | 5.02 (35) |
| 1.25 (39) | 254 | 2.66 (15) | 6.76 (35) |
| 1.4 (39) | 295 | 3.08 (15) | 8.81 (35) |
| 1.5 (39) | 324 | 3.37 (15) | 1.03 (36) |
| 1.7 (39) | 383 | 4.00 (15) | 1.38 (36) |
| 2.0 (39) | 475 | 5.04 (15) | 2.02 (36) |
| 2.5 (39) | 639 | 7.02 (15) | 3.40 (36) |
| 3.0 (39) | 814 | 9.36 (15) | 5.20 (36) |
| При |
|||
г) Учет конечной температуры.
Учет температурных эффектов при плотностях, когда существенно ядерное
взаимодействие, сделан для
![]() с помощью обобщения
методов, применявшихся при исследовании холодного вещества [465]
(см. также [314]). В равновесии рассматривались протоны, нейтроны,
ядра гелия, один тип тяжелых ядер, для которых находился минимум полной
энергии. Ввиду свободного улета нейтрино и отсутствия равновесия по
бета-процессам, задавалось отношение
с помощью обобщения
методов, применявшихся при исследовании холодного вещества [465]
(см. также [314]). В равновесии рассматривались протоны, нейтроны,
ядра гелия, один тип тяжелых ядер, для которых находился минимум полной
энергии. Ввиду свободного улета нейтрино и отсутствия равновесия по
бета-процессам, задавалось отношение
![]() .
Выражения всех видов энергии, входящих в
.
Выражения всех видов энергии, входящих в ![]() из (4.6) и
из (4.8), записывались с учетом температурных поправок и к
из (4.6) и
из (4.8), записывались с учетом температурных поправок и к ![]() добавлялась энергия движения ядер, связанная с конечной температурой,
а также энергии ядер гелия. К независимым величинам, которые являются
аргументами функции
добавлялась энергия движения ядер, связанная с конечной температурой,
а также энергии ядер гелия. К независимым величинам, которые являются
аргументами функции ![]() в (4.6), при конечной температуре
добавляются
в (4.6), при конечной температуре
добавляются ![]() -концентрация свободных протонов и
-концентрация свободных протонов и ![]() - концентрация ядер гелия, которая определяется из условия равновесия
относительно разбиения на протоны и нейтроны типа (3.3), но с учетом
конечного объема (задаваемого) ядер гелия. Для определения
- концентрация ядер гелия, которая определяется из условия равновесия
относительно разбиения на протоны и нейтроны типа (3.3), но с учетом
конечного объема (задаваемого) ядер гелия. Для определения ![]() добавлялось условие равновесия по обмену протонами между ядрами и
протонами в газе. На рис.8 из [456] представлены химические свойства
при больших температурах и плотностях для
добавлялось условие равновесия по обмену протонами между ядрами и
протонами в газе. На рис.8 из [456] представлены химические свойства
при больших температурах и плотностях для ![]() . Интересно,
что при больших плотностях
. Интересно,
что при больших плотностях
![]() , когда
ядра начинают занимать больше половины объема, вместо ядер, погруженных
в менее плотный нуклонный газ, возникают шарики менее плотного вещества
(пузыри), погруженные в более плотную ядерную материю. Важный вывод,
следующий из данных расчетов, состоит в сохранении ядер до очень высоких
температур
, когда
ядра начинают занимать больше половины объема, вместо ядер, погруженных
в менее плотный нуклонный газ, возникают шарики менее плотного вещества
(пузыри), погруженные в более плотную ядерную материю. Важный вывод,
следующий из данных расчетов, состоит в сохранении ядер до очень высоких
температур
![]() , что является
следствием учета ядерных взаимодействий и влияния окружающего газа
на свойства ядер. В [456] отмечалось, что диаграмма на рис. 8
мало чувствительна к изменению
, что является
следствием учета ядерных взаимодействий и влияния окружающего газа
на свойства ядер. В [456] отмечалось, что диаграмма на рис. 8
мало чувствительна к изменению ![]() в пределах
в пределах
![]() .
Учет различных типов тяжелых ядер, одновременно присутствующих в равновесии
[346], также слабо влияет на полученные результаты [456].
На рис. 9 и 10 из [456] приведены изэнтропы вещества и зависимость
показателя адиабаты
.
Учет различных типов тяжелых ядер, одновременно присутствующих в равновесии
[346], также слабо влияет на полученные результаты [456].
На рис. 9 и 10 из [456] приведены изэнтропы вещества и зависимость
показателя адиабаты
![]() для этих
изэнтроп. Видно, что существование ядер заметно уменьшает
для этих
изэнтроп. Видно, что существование ядер заметно уменьшает ![]() по сравнению с нуклонным газом при ненулевой энтропии. Как видно из
рис. 8, при плотности, больше ядерной, вещество всегда однородно.
по сравнению с нуклонным газом при ненулевой энтропии. Как видно из
рис. 8, при плотности, больше ядерной, вещество всегда однородно.
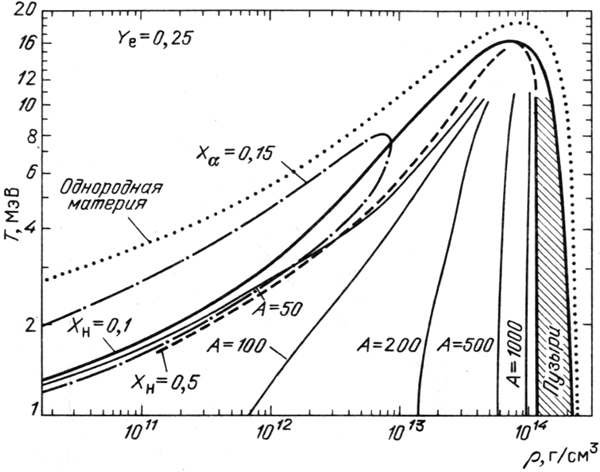 |
| Рис. 8.
Химические свойства вещества при высоких температурах и плотностях
для |
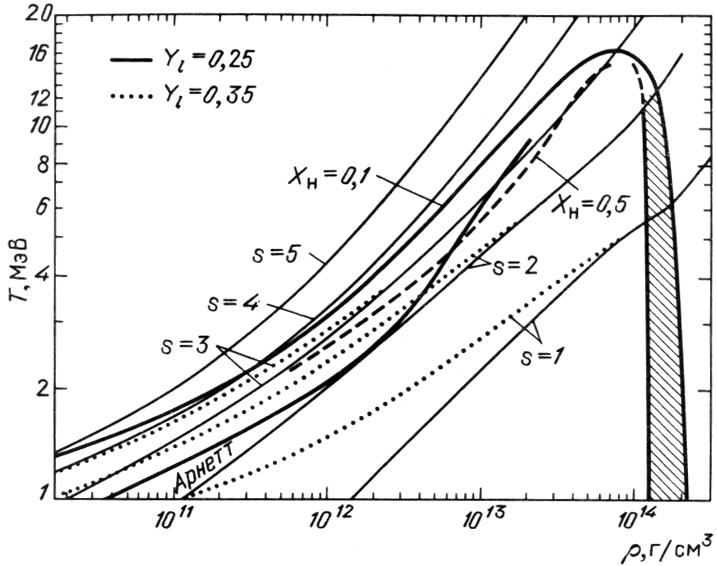 |
| Рис. 9.
Адиабаты с указанными значениями безразмерной энтропии |
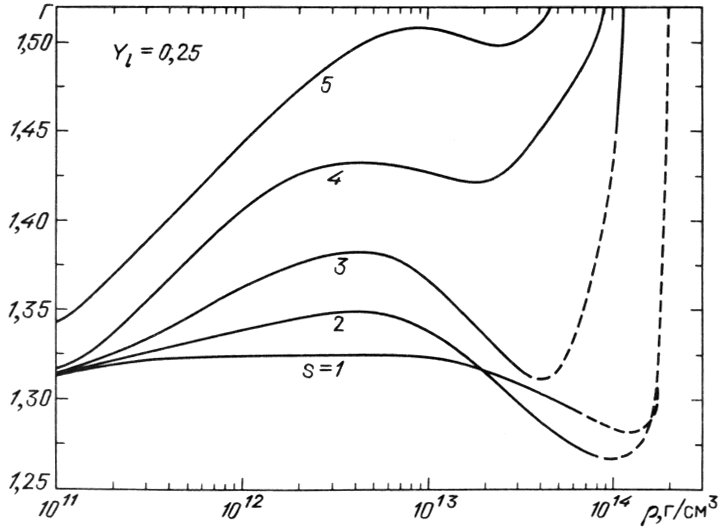 |
| Рис. 10.
Зависимость показателя адиабаты
|
Энергия Ферми идеального нейтронного газа, определяемая аналогично (2.21), есть
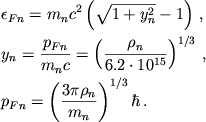 |
(4.10) |
При
![]() имеем
имеем
![]() и
и
![]() . Максимальные температуры, достигаемые
при гравитационном коллапсе, обычно не превышают
. Максимальные температуры, достигаемые
при гравитационном коллапсе, обычно не превышают
![]() ,
поэтому при
,
поэтому при
![]() температурные поправки к уравнению
состояния несущественны.
температурные поправки к уравнению
состояния несущественны.
д) Неравновесная нейтронизация при увеличении плотности в холодном веществе.
Равновесие по ядерному составу достигается в веществе при высоких
температурах, когда открыты все каналы реакций. По мере остывания,
большинство каналов реакций закрывается и в холодном веществе достижение
СМЭ, строго говоря, невозможно. Вещество при малых температурах всегда
находится в неравновесном состоянии, однако степень не равновесности
и характер ее зависят от пути, которым вещество пришло к состоянию
с данными ![]() и
и ![]() . В [60, 61, 287] рассмотрены
два возможных пути: сжатие холодного вещества и остывание вещества
при данной плотности с неравновесными составами, возникающими при
этом.
. В [60, 61, 287] рассмотрены
два возможных пути: сжатие холодного вещества и остывание вещества
при данной плотности с неравновесными составами, возникающими при
этом.
Рассмотрим сжатие холодного вещества. Пусть при малых ![]() вещество состоит из самого стабильного элемента
вещество состоит из самого стабильного элемента ![]() и медленно
сжимается при температуре, близкой к нулю. Когда плотность достигает
величины
и медленно
сжимается при температуре, близкой к нулю. Когда плотность достигает
величины
![]() ,
,
![]() ,
становится энергетически выгодным захват электрона ядром
,
становится энергетически выгодным захват электрона ядром ![]() 7. Ввиду меньшей устойчивости нечетно-нечетных ядер, за первым захватом
сразу следует второй и идет цепочка реакций
7. Ввиду меньшей устойчивости нечетно-нечетных ядер, за первым захватом
сразу следует второй и идет цепочка реакций
| (4.11) |
Для второй реакции из (4.11) величина
![]() [99]. При
[99]. При
![]() она проходит неравновесно
и сопровождается нагревом ([56], см. гл. 5), которым пренебрегаем
ввиду того, что он не влияет на формирование химического состава.
После образования
она проходит неравновесно
и сопровождается нагревом ([56], см. гл. 5), которым пренебрегаем
ввиду того, что он не влияет на формирование химического состава.
После образования ![]() в ходе дальнейшего сжатия становятся
энергетически выгодными превращения
в ходе дальнейшего сжатия становятся
энергетически выгодными превращения
![]() и т.д., пока не образуется ядро с энергией отрыва последнего нейтрона,
близкой к нулю
и т.д., пока не образуется ядро с энергией отрыва последнего нейтрона,
близкой к нулю
![]() . После этого повышение плотности
и захват электронов сопровождаются холодным испарением нейтронов из
ядер и уменьшением
. После этого повышение плотности
и захват электронов сопровождаются холодным испарением нейтронов из
ядер и уменьшением ![]() наряду с
наряду с ![]() . Ввиду различия в свойствах
четных и нечетных ядер, часть испаряющихся нейтронов уносит энергию
. Ввиду различия в свойствах
четных и нечетных ядер, часть испаряющихся нейтронов уносит энергию
![]() 1 МэВ/нейтрон, идущую на нагрев вещества [78].
1 МэВ/нейтрон, идущую на нагрев вещества [78].
В процессе неравновесной нейтронизации число ядер, приходящихся на
один барион, не меняется. Если ![]() - атомная масса начального
ядра, то при данной плотности концентрации ядер и электронов (с учетом
электронейтральности) запишутся в виде
- атомная масса начального
ядра, то при данной плотности концентрации ядер и электронов (с учетом
электронейтральности) запишутся в виде
| (4.12) |
Здесь масса ядра приближенно принята равной ![]() , а плотность
, а плотность
![]() ,
, ![]() полная концентрация барионов.
До начала испарения нейтронов при
полная концентрация барионов.
До начала испарения нейтронов при ![]() заряд ядра
заряд ядра ![]() остается постоянным в интервале плотностей, где выполняется неравенство
остается постоянным в интервале плотностей, где выполняется неравенство
| (4.13) |
Когда первое соотношение в (4.13) обращается в равенство, начинается
очередной захват электрона при постоянных
![]() и
и
![]() в интервале плотностей
в интервале плотностей
![]() :
:
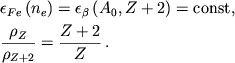 |
(4.14) |
Свойства вещества при холодной нейтронизации до начала испарения нейтронов приведены в табл. 10, где использовались ядерные данные из [379]. После начала испарения нейтронов концентрация их определяется соотношением
| (4.15) |
Испарение нейтрона из ядра при наличии свободных нейтронов допустимо, если энергия вылетающих нейтронов превышает их энергию Ферми (4.10). Условие испарения после очередного захвата электрона в условиях (4.14) запишется в виде
| (4.16) |
Ввиду колебания функции ![]() в зависимости от четности
в зависимости от четности
![]() и
и ![]() , протекает сразу цепочка реакций
, протекает сразу цепочка реакций
| (4.17) |
|
|
|
|
|
|
|
| 0.012 | 56; 24 | 3.81 | 0 | 5.5 (-4) | 0 |
| 0.14 | 56; 22 | 8.83 | 0 | 0.014 | 0 |
| 0.57 | 56; 20 | 14.0 | 0 | 0.080 | 0 |
| 1.6 | 56; 18 | 19.3 | 0 | 0.28 | 0 |
| 3.098 | 54; 18 | 23.84 | 0.069 | 0.569 | 3(-4) (6.5) |
| 3.9 | 56; 16 | 25.2 | 0 | 0.73 | 0 |
| 5.01 | 56; 16 | 26.98 | 0 | 0.933 | |
| 6.17 | 54; 16 | 28.85 | 0.09 | 1.20 | |
| 6.233 | 48; 16 | 29.52 | 0.232 | 1.25 | 0.0059 (5.7) |
| 7.24 | 46; 16 | 29.19 | 0.26 | 1.29 | |
| 7.664 | 42; 14 | 29.66 | 0.468 | 1.41 | 0.0344 (3.6) |
| 9.689 | 36; 12 | 30.47 | 0.693 | 1.75 | 0.0921 (4.1) |
| 10.1 | 56; 14 | 31.78 | 0 | 1.97 | 0 |
| 10.23 | 40; 12 | 31.00 | 0.44 | 1.66 | |
| 12.1 | 48; 12 | 32.06 | 0.43 | 2.07 | 0.029 |
| 12.88 | 35; 10 | 31.60 | 0.58 | 1.86 | |
| 14.13 | 32; 9 | 31.47 | 0.65 | 1.86 | |
| 14.88 | 30; 10 | 31.36 | 0.987 | 2.12 | 0.422 (4.5) |
| 15.0 | 40; 10 | 32.35 | 0.79 | 2.25 | 0.13 |
| 16.8 | 36; 9 | 32.50 | 0.9 | 2.38 | 0.23 |
| 17.43 | 24; 8 | 32.47 | 1.41 | 2.48 | 0.537 (5.2) |
| 19.2 | 32; 8 | 32.64 | 1.22 | 2.59 | 0.39 |
| 22.2 | 28; 7 | 32.78 | 1.49 | 2.88 | 0.65 |
| 25.65 | 18; 6 | 33.47 | 2.04 | 3.57 | 1.36 (6.0) |
| 26.3 | 24; 6 | 32.92 | 1.82 | 3.35 | 1.07 |
| 44.12 | 12; 4 | 35.38 | 2.52 | 6.06 | 3.31 (7.8) |
В [560] отмечена важность пикноядерных реакций в ходе холодной
не равновесной нейтронизации ввиду того, что скорость этих реакций
быстро растет с ростом плотности (см. гл. 4). При
![]() ядра с
ядра с
![]() , образующиеся
из ядер
, образующиеся
из ядер ![]() , сливаются и после захвата двух электронов
и испарения восьми нейтронов, образуются ядра с
, сливаются и после захвата двух электронов
и испарения восьми нейтронов, образуются ядра с
![]() .
В [560] не рассматривался тепловой эффект этой и последующих реакций
слияния. Холодная неравновесная нейтронизация доведена до
.
В [560] не рассматривался тепловой эффект этой и последующих реакций
слияния. Холодная неравновесная нейтронизация доведена до
![]() с образованием ядра
с образованием ядра
![]() (ср. с ядром
(ср. с ядром
![]() из табл. 8 или
из табл. 8 или ![]() из рис. 7 для равновесного состава
при той же плотности). Не исключено, что выделение тепла при пикноядерных
реакциях с последующим быстрым неравновесным захватом электронов и
испарением нейтронов может достаточно повысить температуру для установления
ядерного состава, близкого к равновесному.
из рис. 7 для равновесного состава
при той же плотности). Не исключено, что выделение тепла при пикноядерных
реакциях с последующим быстрым неравновесным захватом электронов и
испарением нейтронов может достаточно повысить температуру для установления
ядерного состава, близкого к равновесному.
Энергия отрыва последнего протона
| (4.18) |
| (4.19) |
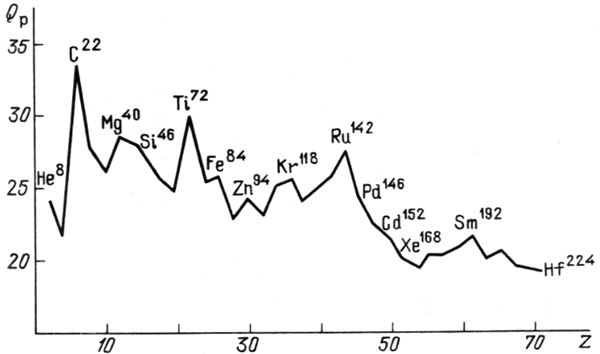 |
| Рис. 11.
Энергия отрыва протона |
Пренебрегая энергией Ферми свободных нейтронов и считая, что нейтронизация
с испарением нейтронов идет вдоль линии ![]() , получим из
(4.14) с учетом (2.21), (4.12) и (4.19) соотношение для определения
, получим из
(4.14) с учетом (2.21), (4.12) и (4.19) соотношение для определения
![]() ,
,
![]() :
:
![\begin{displaymath}
\left[ 1+\left( \frac{Z_{\rho }}{10^{6}A_{0}}\right) ^{2/3}\right] ^{^{1/2}}=1.96\left( 33-\frac{Z}{7}\right) +2.53 ;
\quad A=4Z \end{displaymath}](https://images.astronet.ru/pubd/2006/01/25/0001211125/tex/formula558.gif) |
(4.20) |
Здесь учтено, что
![]() МэВ,
МэВ,
![]() МэВ.
Расчеты с использованием (4.20) также приведены в табл. 10, откуда
видно, что различие в давлении
МэВ.
Расчеты с использованием (4.20) также приведены в табл. 10, откуда
видно, что различие в давлении
![]() для всех
трех способов не превышает 20%. В то же время это давление более
чем в полтора раза превышает равновесное давление при той же плотности
(табл. 7).
для всех
трех способов не превышает 20%. В то же время это давление более
чем в полтора раза превышает равновесное давление при той же плотности
(табл. 7).
е) Неравновесный состав при остывании горячего плотного вещества.
Когда температура в остывающем веществе станет меньше
![]() ,
реакции между заряженными частицами резко замедляются и концентрация
ядер замораживается. В этих условиях возможно протекание реакций с
нейтронами, фотоотщепление и захват нейтронов,
,
реакции между заряженными частицами резко замедляются и концентрация
ядер замораживается. В этих условиях возможно протекание реакций с
нейтронами, фотоотщепление и захват нейтронов, ![]() распады
при
распады
при
![]() и
и ![]() -захваты
при
-захваты
при
![]() . В условиях кинетического
равновесия по бета-процессам (3.6) с
. В условиях кинетического
равновесия по бета-процессам (3.6) с
![]() , в
веществе имеется большой избыток свободных нейтронов [224]. При
конечной температуре ядра могут присоединять нейтроны и отщеплять
их, если
, в
веществе имеется большой избыток свободных нейтронов [224]. При
конечной температуре ядра могут присоединять нейтроны и отщеплять
их, если
| (4.21) |
В условиях избытка нейтронов ![]() процесс формирования
неравновесного химического состава при быстром остывании вещества
представлен на рис. 12 из [61, 287]. Плоскость
процесс формирования
неравновесного химического состава при быстром остывании вещества
представлен на рис. 12 из [61, 287]. Плоскость
![]() для ядер разбита на три области:
для ядер разбита на три области:
I область с ![]() ,
,
II область с
![]() ,
,
![]() .
.
III область с
![]() ,
,
![]() .
.
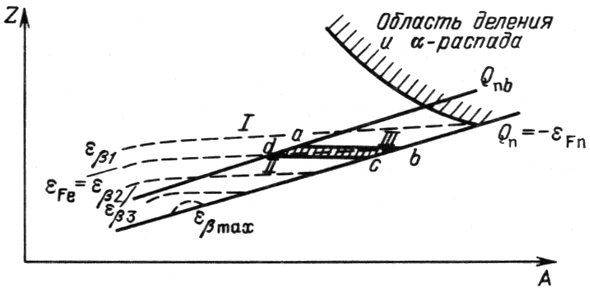 |
| Рис. 12.
Образование химического состава при остывании на стадии ограниченного
равновесия. Линия |
При высокой концентрации нейтронов существующие ядра быстро перейдут
из области I в области II и III из-за нейтронного захвата. В областях
II и III имеется равновесие по отношению к захвату и отщеплению нейтронов.
В области II бета-распады приводят к росту Z и ядра переходят в область
выше линии ![]() . В области III бета-захваты уменьшают
. В области III бета-захваты уменьшают ![]() и переводят ядра в область ниже линии
и переводят ядра в область ниже линии ![]() . Таким образом, в
условиях ограниченного равновесия при
. Таким образом, в
условиях ограниченного равновесия при
![]() ,
когда температурные эффекты не влияют на бета-процессы, ядерный состав
определяется узкой областью aecd на плоскости
,
когда температурные эффекты не влияют на бета-процессы, ядерный состав
определяется узкой областью aecd на плоскости ![]() (рис. 12).
Выход за пределы этой области не происходит из-за отсутствия допустимых
бета-процессов и фотоотщеплений нейтронов. При
(рис. 12).
Выход за пределы этой области не происходит из-за отсутствия допустимых
бета-процессов и фотоотщеплений нейтронов. При
![]() остается только одно ядро на границе (4.16).
остается только одно ядро на границе (4.16).
Если пренебречь
![]() и учесть (4.18) и (4.19), то
ядерный состав можно приближенно найти из соотношений, аналогичных
(4.20),
и учесть (4.18) и (4.19), то
ядерный состав можно приближенно найти из соотношений, аналогичных
(4.20),
![\begin{displaymath}
A=4Z , \quad Z=7\left\{ 33-0.511\left[ \left( \frac{\rho }{\mu _{Z}10^{6}}\right) ^{2/3}+1\right] ^{1/2}+1.293\right\} .
\end{displaymath}](https://images.astronet.ru/pubd/2006/01/25/0001211125/tex/formula577.gif) |
(4.22) |
Зависимость ![]() при
при ![]() приведена на рис.
13. При
приведена на рис.
13. При
![]() образуется
ядро с
образуется
ядро с ![]() , обладающее
, обладающее
![]() , а при
, а при
![]() образуется ядро
с
образуется ядро
с ![]() , для которого
, для которого
![]() и [164] время
деления, зависящее от
и [164] время
деления, зависящее от ![]() , есть
, есть
![]() лет. При
лет. При
![]() величина
величина ![]() растет, а
время деления уменьшается. Ядерное деление, а также альфа-распад приводят
к росту числа зародышевых ядер. Таким образом, при
растет, а
время деления уменьшается. Ядерное деление, а также альфа-распад приводят
к росту числа зародышевых ядер. Таким образом, при
![]() или
или
![]() химический состав может приблизиться к
равновесному в состоянии СМЭ. Существенная неравновесность при остывании
возможна только при
химический состав может приблизиться к
равновесному в состоянии СМЭ. Существенная неравновесность при остывании
возможна только при
![]() .
.
 |
| Рис. 13.
Зависимость |
Отличие неравновесности, образующейся при остывании, от той, которая
образуется при холодной нейтронизации, имеется, в основном, при меньших
плотностях, где для горячего случая получаются очень большие ![]() ,
см. табл. 10 и рис. 13. В то же время в обоих вариантах имеются принципиальные
отличия от СМЭ, где
,
см. табл. 10 и рис. 13. В то же время в обоих вариантах имеются принципиальные
отличия от СМЭ, где ![]() увеличивается с ростом плотности,
в то время как в обоих неравновесных составах
увеличивается с ростом плотности,
в то время как в обоих неравновесных составах ![]() быстро
падает с ростом плотности.
быстро
падает с ростом плотности.
ж) Термодинамические свойства вещества при учете кулоновского взаимодействия. Кулоновские взаимодействия в обычном веществе являются основными, определяющими агрегатное состояние, степени ионизации и поправки к термодинамическим функциям. В разреженных газах взаимодействия в основном локализованы внутри атомов и неполностью ободранных ионов. При нахождении степени ионизации по формуле Саха (1.8) происходит приближенный учет этого взаимодействия.
Основным параметром, характеризующим степень ионизации в разреженных
газах, является величина
![]() (см. 1).
При уменьшении температуры и росте
(см. 1).
При уменьшении температуры и росте ![]() газ становится
нейтральным, а затем, когда тепловая энергия станет меньше энергии
взаимодействия между атомами, превратится сначала в жидкое, а затем
в твердое кристаллическое тело с упорядоченной структурой, обладающей
минимумом энергии8. При сжатии вещества среднее расстояние между атомами
газ становится
нейтральным, а затем, когда тепловая энергия станет меньше энергии
взаимодействия между атомами, превратится сначала в жидкое, а затем
в твердое кристаллическое тело с упорядоченной структурой, обладающей
минимумом энергии8. При сжатии вещества среднее расстояние между атомами
![]() уменьшается9 и при
уменьшается9 и при
![]() становится порядка размера атома
становится порядка размера атома
![]() в модели Томаса-Ферми (ТФ) [555],
в модели Томаса-Ферми (ТФ) [555],
![]() - Боровский радиус. При
- Боровский радиус. При
![]() начинается ионизация
давлением. Вещество становится полностью ионизованным при
начинается ионизация
давлением. Вещество становится полностью ионизованным при
![]() .
когда межэлектронные расстояния становятся порядка радиуса ближайшей
к ядру электронной орбиты
.
когда межэлектронные расстояния становятся порядка радиуса ближайшей
к ядру электронной орбиты
![]() [71]. Плотность
[71]. Плотность
![]() находится с учетом (2.21) из соотношения
находится с учетом (2.21) из соотношения
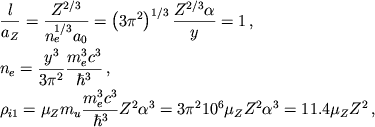 |
(4.23) |
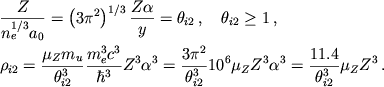 |
(4.24) |
Рассмотрим фазовые превращения и кулоновские поправки к термодинамическим
функциям в плотном, полностью ионизованном веществе. В виду малости
параметра
![]() поправки при
поправки при ![]() можно находить методом последовательных приближений
[3,555]. Основную поправку к кинетической энергии электронов дает
электростатическое взаимодействие ионов в решетке и свободных электронов
между собой, а также обменное взаимодействие электронов. В первом
приближении электроны можно считать расположенными однородно. Энергия
электростатического взаимодействия
можно находить методом последовательных приближений
[3,555]. Основную поправку к кинетической энергии электронов дает
электростатическое взаимодействие ионов в решетке и свободных электронов
между собой, а также обменное взаимодействие электронов. В первом
приближении электроны можно считать расположенными однородно. Энергия
электростатического взаимодействия ![]() наиболее просто рассчитывается
в приближении Вигнера-Зейца (
наиболее просто рассчитывается
в приближении Вигнера-Зейца (![]() ), где учитывается только взаимодействие
ионов и электронов внутри сферической ячейки радиуса
), где учитывается только взаимодействие
ионов и электронов внутри сферической ячейки радиуса ![]()
| (4.25) |
Энергия на одно ядро ![]() в данном приближении есть [3, 555]
в данном приближении есть [3, 555]
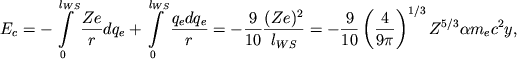 |
(4.26) |
![\begin{displaymath}
\eqalign{
& E_{TF}=-\frac{162}{175}\left( \frac{4}{9\pi }\right) ^{2/3}\sqrt{1+y^{2}}Z^{7/3}\alpha ^{2}m_{e}c^{2}\,, \cr
& E_{cor}=\left[ 0.031\ln \left( \frac{e^{2}m_{e}}{\hbar ^{2}}l_{WS}\right) -0.048\right] Z\alpha ^{2}m_{e}c^{2}\,. \cr }
\end{displaymath}](https://images.astronet.ru/pubd/2006/01/25/0001211125/tex/formula861.gif) |
(4.27) |
Последний член становится существенным при уменьшении плотности. Энергия обменного взаимодействия в общем случае есть [555]
![\begin{displaymath}
\hbox{%
\begin{tabular}{l}
$\displaystyle{ \varphi \left( y\right) =\frac{1}{4y^{4}}\left[ \frac{9}{4}+3\left( \beta ^{2}-\frac{1}{\beta ^{2}}\right) \ln \beta -6\left( \ln \beta \right) ^{2}-\left( \beta ^{2}+\frac{1}{\beta ^{2}}\right) -\frac{1}{8}\left( \beta ^{4}+\frac{1}{\beta ^{4}}\right) \right] , }$ \\
$\displaystyle{ \beta =y+\sqrt{1+y^{2}} ; }$ \\
$\displaystyle{ \varphi \left( y\right) = \left\{ \begin{array}{cl} 1 & \quad \mbox{при~} y\ll 1 , \\ -1/2 & \quad \mbox{при~} y\gg 1 . \\ \end{array} \right. }$ \\
\end{tabular}}
\end{displaymath}](https://images.astronet.ru/pubd/2006/01/25/0001211125/tex/formula862.gif) |
(4.28) |
В нерелятивистском пределе ![]() приведена в [3]. Таким
образом, основные поправки к кинетической энергии холодного газа (2.22)
за счет кулоновского взаимодействия для единицы массы равны с учетом
(2.19)
приведена в [3]. Таким
образом, основные поправки к кинетической энергии холодного газа (2.22)
за счет кулоновского взаимодействия для единицы массы равны с учетом
(2.19)
![\begin{displaymath}
\eqalign{ E_{q}=&\frac{1}{Am_{u}}\left( E_{c}+E_{TF}+E_{cor}+E_{ex}\right) = \cr & =\left\{ -\frac{3}{10\pi ^{2}}\left( \frac{4}{9\pi }\right) ^{1/3}\alpha Z^{2/3}y-\frac{54}{175\pi ^{2}}\left( \frac{4}{9\pi }\right) ^{2/3}\alpha ^{2}Z^{4/3}\sqrt{1+y^{2}}+ \right. \cr & \left. +\frac{0.031\alpha ^{2}}{3\pi ^{2}}\ln \left[ \left( \frac{9\pi }{4}\right) ^{1/3}\frac{\alpha Z^{1/3}}{y}\right] -\frac{0.016}{\pi ^{2}}\alpha ^{2}-\frac{\alpha }{4\pi ^{3}}y\varphi \left( y\right) \right\} \frac{m^{4}_{e}c^{5}}{\hbar ^{3}}\frac{y^{3}}{\rho }\,. \cr }
\end{displaymath}](https://images.astronet.ru/pubd/2006/01/25/0001211125/tex/formula863.gif) |
(4.29) |
Из термодинамического соотношения
![]() ,
,
![]() находим поправку к
давлению
находим поправку к
давлению
![\begin{displaymath}
\eqalign{ P_{q}& =P_{c}+P_{TF}+P_{cor}+P_{ex}= \cr & =-\frac{m^{4}_{e}c^{5}}{\hbar ^{3}}y^{3}\left[ \frac{1}{10\pi ^{2}}\left( \frac{4}{9\pi }\right) ^{1/3}\alpha Z^{2/3}y+\frac{18}{175\pi ^{2}}\left( \frac{4}{9\pi }\right) ^{2/3}\alpha ^{2}Z^{4/3}\frac{y^{2}}{\sqrt{1+y^{2}}}-\frac{0.031}{9\pi ^{2}}\alpha ^{2}+\frac{\alpha }{4\pi ^{3}}\frac{\chi \left( y\right) }{y^{3}}\right]\,, \cr }
\end{displaymath}](https://images.astronet.ru/pubd/2006/01/25/0001211125/tex/formula864.gif) |
(4.30) |
![\begin{displaymath}
\hbox{%
\begin{tabular}{l}
$\displaystyle{ \chi \left( y\right) =\frac{y^{4}}{3}\frac{d}{dy}\left[ y\varphi \left( y\right) \right] =\frac{1}{32}\left( \beta ^{4}+\frac{1}{\beta ^{4}}\right) +\frac{1}{4}\left( \beta ^{2}+\frac{1}{\beta ^{2}}\right) -\frac{9}{16}-\frac{3}{4}\left( \beta ^{2}-\frac{1}{\beta ^{2}}\right) \ln \beta +\frac{3}{2}\left( \ln \beta \right) ^{2}- }$ \\
$\displaystyle{ \qquad\qquad -\frac{y}{3}\left( 1+\frac{y}{\sqrt{1+y^{2}}}\right) \left[ \frac{1}{8}\left( \beta ^{2}-\frac{1}{\beta ^{5}}\right) -\frac{1}{4}\left( \beta -\frac{1}{\beta ^{3}}\right) -\frac{3}{2}\left( \beta +\frac{1}{\beta ^{3}}\right) \ln \beta +\frac{3}{\beta }\ln \beta \right] , }$ \\[3mm]
$\displaystyle{ \chi \left( y\right) =\left\{ \begin{array}{cl} y^{4}/3 & \quad \mbox{при~} y\ll 1 , \\ -y^{4}/6 & \quad \mbox{при~} y\gg 1 . \\
\end{array}\right. }$ \\
\end{tabular}}
\end{displaymath}](https://images.astronet.ru/pubd/2006/01/25/0001211125/tex/formula865.gif)
Отсюда в предельных случаях имеем с учетом (2.32) и (2.33)
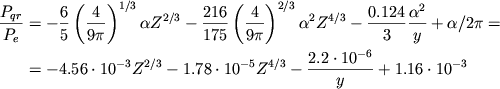 |
(4.31) |
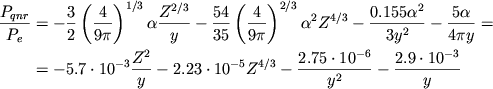 |
(4.32) |
| (4.33) |
| (4.34) |
при
В силу квантовых свойств вещества ионы в решетке при абсолютном нуле
совершают колебания с частотой, определяемой взаимодействием с электронами.
В ![]() приближении возвращающая сила, действующая на ион со стороны
электронов в ячейке при отклонении от равновесия, есть
приближении возвращающая сила, действующая на ион со стороны
электронов в ячейке при отклонении от равновесия, есть
что приводит к частоте гармонических колебаний [125, 555]
| (4.35) |
| (4.36) |
При ![]() кулоновский кристалл разрушается уже при нулевой
температуре за счет квантовых колебаний. При этом необходимы слишком
большие плотности
кулоновский кристалл разрушается уже при нулевой
температуре за счет квантовых колебаний. При этом необходимы слишком
большие плотности
![]() ,
так что в холодных звездах нулевые колебания не разрушают кристаллической
структуры.
,
так что в холодных звездах нулевые колебания не разрушают кристаллической
структуры.
Более реальным является разрушение кристалла тепловыми движениями
ионов [485, 620]. Плавление кристалла происходит при ![]() ,
когда кинетическая энергия колебаний
,
когда кинетическая энергия колебаний ![]() составляет ~
1/150 от кулоновской энергии
составляет ~
1/150 от кулоновской энергии ![]() ячейки [544, 245, 578]11. Имеем с учетом (4.26)
ячейки [544, 245, 578]11. Имеем с учетом (4.26)
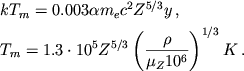 |
(4.37) |
Термодинамические свойства кристаллических тел хорошо известны [145].
При малых температурах возбуждаются только степени свободы, соответствующие
длинным волнам (малым частотам). Эти моды колебаний (фононы) обладают
свойствами, аналогичными фотонному газу. Напротив, при больших температурах
возбуждаются все возможные моды колебаний. При этом энергия колебаний
кристалла в два раза больше кинетической энергии вещества в газовом
состоянии при той же температуре. В общем случае для тепловой энергии
ионной решетки на единицу массы справедлива интерполяционная формула
Дебая [145]
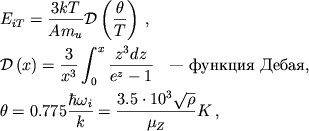 |
(4.38) |
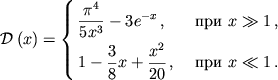 |
(4.39) |
Энтропия единицы массы и давление, связанные с ионным кристаллом,
равны [145]
| (4.40) |
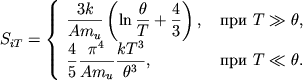 |
(4.41) |
В зависимости от соотношения между температурами ![]() ,
, ![]() и
и ![]() имеем следующие состояния ионизованного вещества:
имеем следующие состояния ионизованного вещества:
|
|
|
|
|
|
|
| Квантовый (вырожденный) кристалл | Классический ионный кристалл | Классическая жидкость (неидеальная плазма) | Квантовая жидкость | ||
Плавление ионного кристалла при
![]() сопровождается
выделением тепла, а при дальнейшем росте температуры происходит переход
к идеальному газу с
сопровождается
выделением тепла, а при дальнейшем росте температуры происходит переход
к идеальному газу с
![]() . Согласно
[544, 245, 578] приближение идеального газа становится применимым при:
. Согласно
[544, 245, 578] приближение идеального газа становится применимым при:
| (4.42) |
В промежутке
![]() можно использовать интерполяцию.
Вопрос о теплоте плавления не вполне ясен. В [485] приводятся
аргументы в пользу очень малой теплоты плавления при постоянных
можно использовать интерполяцию.
Вопрос о теплоте плавления не вполне ясен. В [485] приводятся
аргументы в пользу очень малой теплоты плавления при постоянных ![]() и
и ![]() . В [620] из других соображений предполагается,
что фазовый переход относится к первому роду и теплота плавления решетки
при постоянных
. В [620] из других соображений предполагается,
что фазовый переход относится к первому роду и теплота плавления решетки
при постоянных ![]() и
и ![]() есть
есть
| (4.43) |
Строгого решения этой проблемы не сделано.
Наиболее сложен для количественного описания промежуточный интервал
плотностей
![]() , где степень ионизации
определяется как тепловой энергией, так и давлением. В ТФ приближении
процесс ионизации холодного вещества давлением исследован в [126].
Оболочечные поправки приводят к скачкам давления при каждой последующей
ионизации, при плотности
, где степень ионизации
определяется как тепловой энергией, так и давлением. В ТФ приближении
процесс ионизации холодного вещества давлением исследован в [126].
Оболочечные поправки приводят к скачкам давления при каждой последующей
ионизации, при плотности
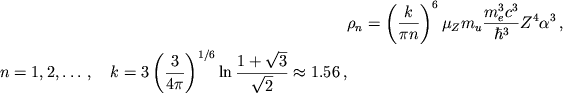 |
(4.44) |
Зависимость немонотонной поправки к давлению от плотности задается
формулой [126]
| (4.45) |
| (4.46) |
| (4.47) |
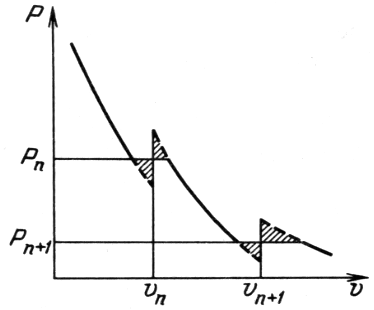 |
| Рис. 14.
Схематическая зависимость давления от удельного объема при учете
оболочечных эффектов. Постоянные уровни давления |
Термодинамические свойства смеси водорода и гелия при конечной температуре
с учетом взаимодействия и ионизации давлением изучались в [403].
Учитывались соединения ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
, ![]() . Для данной температуры
. Для данной температуры ![]() и полного числа ионов
и полного числа ионов ![]() в объеме
в объеме ![]() вычисляется свободная
энергия
вычисляется свободная
энергия ![]() в виде
в виде
| (4.48) |
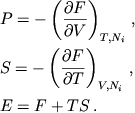 |
(4.49) |
Кулоновское взаимодействие учитывается здесь также в виде поправок
к идеальному газу
| (4.50) |
На основе ТФ теории с дебай-хьюккелевским потенциалом вокруг ядра
(ТФДХ) имеем [403]
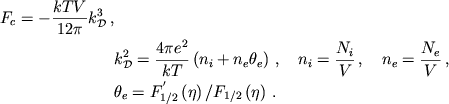 |
(4.51) |
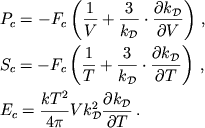 |
(4.52) |
Результаты ТФДХ рассмотрения верны при
| (4.53) |
Для определения степени ионизации используется уравнение Саха, в котором учитывается, в дополнение к (1.8), конечная степень вырождения свободных электронов, влияющая на их химический потенциал. Сдвиг уровней ионов и молекул при учете экранирующего ДХ потенциала приводит к уменьшению числа связанных состояний и уменьшении их глубины. Их учет в формуле Саха отражает ионизацию давлением. В целом, учет ионизации давлением сводится к сложной самосогласованной проблеме, в которой концентрация свободных электронов пе и ионов и,- определяет ДХ радиус и потенциал, а те, в свою очередь, определяют концентрацию посредством сдвига уровней, входящих в уравнение Саха. Задача осложняется отсутствием аналитических решений для уравнения Шредингера с ДХ потенциалом [240], поэтому необходимы численные расчеты. Результаты таких расчетов, выполненных в [403], представлены на рис. 15 и 16. Таблицы уравнения состояния с учетом кулоновского взаимодействия, рассчитанные аналогичным способом, даны в [358].
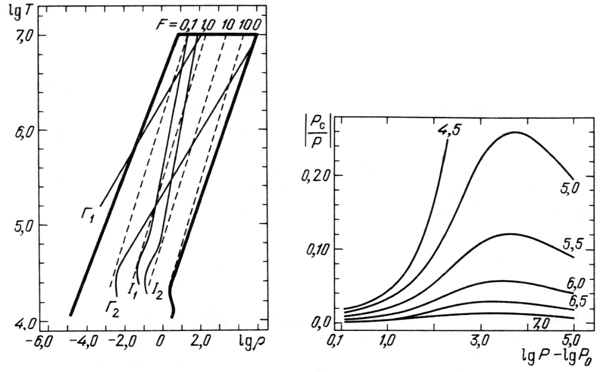 |
| Рис. 15.
Область на плоскости |
| Рис. 16.
Отношение кулоновской поправки к давлению к полному давлению
при T = const. На каждой кривой указана величина |
Задача. Сделать гладкую интерполяцию уравнения состояния холодного вещества нейтронных звезд.
Решение [14]. Гладкая с первой производной интерполяция
уравнения состояния ![]() из табл. 9 [479] определяется
следующими формулами (
из табл. 9 [479] определяется
следующими формулами (![]() - полная плотность массы-энергии
с учетом взаимодействия):
- полная плотность массы-энергии
с учетом взаимодействия):
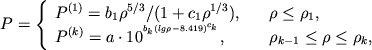 |
(1) |
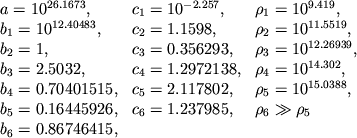
Непрерывность производных ![]() в точках
в точках
![]() из (1) достигается с помощью сглаживания в виде
из (1) достигается с помощью сглаживания в виде
![\begin{displaymath}
P(\rho )=\left\{ \eqalign{ & P^{(k)},\quad \rho \in \left[ \rho _{k-1}+\xi _{k-1},\rho _{k}-\xi _{k}\right], \quad k=1,2,...6, \cr & \theta _{k}P^{(k)}+(1-\theta _{k})P^{(k+1)}, \quad \rho \in \left[ \rho _{k}-\xi _{k}\,,\right. \cr & \left.\rho _{k}+\xi _{k}\right]\,, \quad \rho _{0}+\xi _{0}=0\,,
}\right. \end{displaymath}](https://images.astronet.ru/pubd/2006/01/25/0001211125/tex/formula889.gif) |
(2) |
<< 3. Уравнение состояния при ... | Оглавление |
|
Публикации с ключевыми словами:
Эволюция звезд - физические процессы
Публикации со словами: Эволюция звезд - физические процессы | |
См. также:
Все публикации на ту же тему >> | |