Rambler's Top100Astronet    
  по текстам   по ключевым словам   в глоссарии   по сайтам   перевод   по каталогу 		 

На первую страницу << 1. Идеальный газ с | Оглавление | 3. Уравнение состояния при ... >>

2. Релятивистский газ с учетом вырождения

В центральных областях звезд, находящихся на поздних стадиях эволюции, а также при взрывах сверхновых кинетическая энергия электронов может стать порядка их энергии покоя, т.е. скорости их приближаются к скорости света:


$$ %\begin{displaymath} %kT\sim m_{e}c^{2} , \quad \left\langle \upsilon _{e}\right\rangle \sim c . %\end{displaymath} kT\sim \mec{}2,\quad \langle v_{\mathrm{e}} \rangle \sim c. $$ (2.1)

При вычислении термодинамических функций необходимо тогда использовать полные релятивистские выражения для энергии и импульса электронов. С другой стороны, плотности могут вырасти настолько, что среднее число частиц в ячейке фазового пространства приближается к единице. При этом необходимо учитывать принцип Паули для электронов (спин = 1/2), число которых в ячейке фазового пространства равно либо нулю, либо единице. Среднее число электронов с энергией \( \epsilon \) в ячейке задается функцией Ферми [145]


$$ %\begin{displaymath} %f_{e}=\left[ 1+exp\left( \frac{\epsilon -\mu _{te}}{kT}\right) \right] ^{-1} %\end{displaymath} f_{\rm e}=\left[1+\exp\left(\epsilon-\mu_{t{\rm e}}\over kT\right) \right]^{-1}, $$ (2.2)

где \( \mu _{te} \) - химический потенциал электронов,


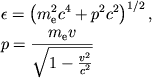$$ %\begin{displaymath} %\epsilon =(m^{2}_{e}c^{4}+p^{2}c^{2})^{1/2} , \quad %p=\frac{m_{e}\upsilon }{\sqrt{1-\frac{\upsilon ^{2}}{c^{2}}}} %\end{displaymath} \eqalign{ &\epsilon=\left(\mec24+p^2c^2\right)^{1/2}, \cr &p={m_{\rm e}v\over \sqrt{1-{v^2\over c^2}}}\quad \cr} $$ (2.3)

- импульс электрона.

Термодинамические функции находятся с помощью интегралов по импульсному пространству (с учетом статистического веса \( g_{e}=2 \)) [145]:


$$ %\begin{displaymath}n_{e}=2\frac{4\pi }{(2\pi \hbar )^{3}}\int _{0}^{\infty }f_{e}p^{2}dp \end{displaymath} n_{\mathrm{e}}=2\pipih\intfe{p^2} $$ (2.4)


$$ %\begin{displaymath}E_{e}=\frac{2}{\rho }\frac{4\pi }{(2\pi \hbar )^{3}}\int _{0}^{\infty }f_{e}\epsilon p^{2}dp \end{displaymath} E_{\mathrm{e}}={2\over \rho}\pipih\intfe{\epsilon p^2}, $$ (2.5)


$$ %\begin{displaymath} %P_{e}=2\frac{4\pi }{(2\pi \hbar )^{3}}\frac{1}{3}\int _{0}^{\infty }f_{e}p\upsilon \cdot p^{2}dp , \quad %\upsilon =\frac{pc}{\sqrt{p^{2}+m^{2}_{e}c^{2}}} , %\end{displaymath} P_{\mathrm{e}}=2\pipih {1\over 3}\intfe{pv\cdot p^2}, \quad v={pc\over \sqrt{p^2+\mec22}}, $$ (2.6)


$$ S_{\mathrm{e}}=-{2\over \rho}\pipih k\intinf\left[f_{\mathrm{e}}\ln f_{\mathrm{e}}+(1-f_{\mathrm{e}}) \ln(1-f_{\mathrm{e}})\right]p^2dp\,. $$ (2.7)

После преобразования интегралов и введения безразмерных величин


$$ %\begin{displaymath} %x=\frac{pc}{kT} , \quad %\alpha =\frac{m_{e}c^{2}}{kT}=\frac{5.93013\cdot 10^{9}K}{T} , \quad %\beta =\frac{\mu _{te}}{kT} %\end{displaymath} x={pc\over kT}, \quad \alpha={\mec{}2\over kT}={5.93013\cdot 10^9K\over T}, \quad \beta={\mu_{t{\rm e}}\over kT} $$ (2.8)

получим


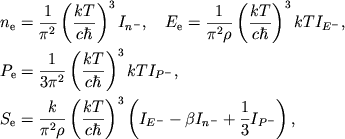$$ %\begin{displaymath} %\hbox{% %\begin{tabular}{l} %$\displaystyle{ n_{e}=\frac{1}{\pi ^{2}}\left( \frac{kT}{c\hbar }\right) ^{3}I_{_{^{n^{-}}}} , }$ %$\displaystyle{ E_{e}=\frac{1}{\pi ^{2}\rho }\left( \frac{kT}{c\hbar }\right) ^{3}kTI_{_{^{E^{-}}}} ,}$ %$\displaystyle{ P_{e}=\frac{1}{3\pi ^{2}}\left( \frac{kT}{c\hbar }\right) ^{3}kTI_{_{^{p^{-}}}} , }$ %$\displaystyle{ S_{e}=\frac{k}{\pi ^{2}\rho }\left( \frac{kT}{c\hbar }\right) ^{3}\left( I_{_{^{E^{-}}}}-\beta I_{_{^{n^{-}}}}+\frac{1}{3}I_{_{^{p^{-}}}}\right) , }$ %\end{tabular}} %\end{displaymath} \eqalign{ &n_{\mathrm{e}}={1\over \pi^2}\ktch I_{n^-},\quad E_{\mathrm{e}}={1\over \pi^2\rho}\ktch kTI_{E^-}, \cr &P_{\mathrm{e}}={1\over 3\pi^2}\ktch kTI_{P^-}, \cr &S_{\mathrm{e}}={k\over \pi^2\rho}\ktch \left(I_{E^-}-\beta I_{n^-}+{1\over 3} I_{P^-}\right), \cr} $$ (2.9)

где

$$ %\begin{displaymath} %\hbox{% %\begin{tabular}{l} %$\displaystyle{ I_{_{^{n^{-}}}}=\int _{0}^{\infty }\frac{x^{2}dx}{1+\exp \left( \sqrt{x^{2}+\alpha ^{2}}-\beta \right) } , }$ %$\displaystyle{ I_{_{^{p^{-}}}}=\int _{0}^{\infty }\frac{x^{4}dx}{\sqrt{x^{2}+\alpha ^{2}}\left[ 1+\exp \left( \sqrt{x^{2}+\alpha ^{2}}-\beta \right) \right] } , }$ %$\displaystyle{ I_{_{^{E^{-}}}}=\int _{0}^{\infty }\frac{\sqrt{x^{2}+\alpha ^{2}}x^{2}dx}{1+\exp \left( \sqrt{x^{2}+\alpha ^{2}}-\beta \right) } . }$ %\end{tabular}} %\end{displaymath} \eqalign{ &I_{n^-}=\intinf{x^2 dx\over \eradxab}, \cr &I_{P^-}=\intinf{x^4 dx\over \radxa\left[\eradxab\right]}, \cr &I_{E^-}=\intinf{\radxa x^2 dx\over \eradxab}. \cr} $$ (2.10)

Когда \( kT\geq 0.1m_{e}c^{2} \), в термодинамическом равновесии необходимо учитывать позитроны. Аннигиляция пары \( e^{-}e^{+} \) приводит к рождению фотонов, химический потенциал которых в равновесии равен нулю, \( \mu_{\Phi}=0 \). Из условия равновесия аннигиляции \( \mu _{te}+\mu _{_{^{te^{+}}}}=\mu_{\Phi}=0 \) следует равенство


$$ %\begin{displaymath}\mu _{_{^{te^{+}}}}=-\mu _{te} \end{displaymath} \mu_{te^+}=-\mu_{te}. $$ (2.11)

Термодинамические функции для позитронов получаются из (2.9), где следует заменить \( \beta \) на \( -\beta \) и использовать интегралы \( I_{_{^{i^{+}}}} \), \( i=n \), \( E \), \( P \), получаемые из \( I_{_{^{i^{-}}}} \) в (2.10) заменой \( \beta \) на \( -\beta \). Нуклоны и ядра часто можно считать невырожденными и нерелятивистскими, поэтому для них, вместе с излучением, имеем


$$ %\begin{displaymath}E_{N,r}=\frac{3}{2}\frac{kT}{\mu _{N}m_{u}}+\frac{aT^{4}}{\rho } \end{displaymath} E_{N,r}={3\over 2}{kT\over \mu_N m_{\mathrm{u}}}+{aT^4\over\rho}, $$ (2.12)


$$ %\begin{displaymath}P_{N,r}=\frac{\rho kT}{\mu _{N}m_{u}}+\frac{aT^{4}}{3} \end{displaymath} P_{N,r}={\rho kT\over \mu_N m_{\mathrm{u}}}+{aT^4\over 3}, $$ (2.13)


$$ %\begin{displaymath}S_{N,r}=\frac{k}{\rho }\Sigma _{i}n_{i}\left\{ \frac{5}{2}+\ln \left[ \left( \frac{m_{i}kT}{2\pi \hbar ^{2}}\right) ^{3/2}\frac{g_{i}}{n_{i}}\right] \right\} +\frac{4}{3}\frac{aT^{3}}{\rho } \end{displaymath} S_{N,r}={k\over \rho}\sum_i n_i\left\{{5\over 2}+\ln\left[\left( m_i kT\over 2\pi\hbar^2\right)^{3/2}{g_i\over n_i}\right]\right\}+ {4\over 3}{aT^3\over\rho}, $$ (2.14)

Здесь рассмотрено полностью ионизованное вещество. Если ядерные реакции не идут и весовые доли элементов неизменны (\( x_{i}=const \)), то аналогично (1.18) имеем


$$ %\begin{displaymath}S_{N}=\frac{k}{\mu _{N}m_{u}}\ln \left( \frac{T^{3/2}}{\rho }\right) + const \end{displaymath} S_{N,r}={k\over \mu_N m_{\mathrm{u}}}\ln\left(T^{3/2}\over \rho \right)+ {\rm const}. $$ (2.15)

В (2.12)-(2.15) использована величина


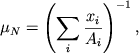$$ %\begin{displaymath}\mu _{N}=\left( \Sigma _{i}\frac{x_{i}}{A_{i}}\right) ^{-1} \end{displaymath} \mu_N=\left(\sum_i {x_i\over A_i}\right)^{-1}, $$ (2.16)

равная среднему числу нуклонов в ядре. Для получения полных выражений термодинамических функция \( P \), \( E \) и \( S \) необходимо просуммировать соответствующие выражения для электронов, позитронов, ядер и излучения. Заряд ядер связан с избытком электронов над позитронами. Имеем


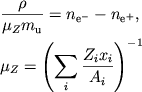$$ \eqalign{ &{\rho\over \mu_Z m_{\mathrm{u}}} = n_{\mathrm{e^-}}-n_{\mathrm{e^+}}, \cr &\mu_Z=\left(\sum_i {Z_i x_i\over A_i}\right)^{-1} \cr} $$ (2.17)

- число нуклонов на один электрон.

Выражение (2.17) с учетом (2.9), (2.10) служит для нахождения зависимости \( \mu _{te}\left( \rho ,T\right) \). Для случая полной ионизации при \( y_{H}=1 \), \( i=Z \) имеем из (1.6), (2.16) и (2.17)


$$ {1\over \mu} = {1\over \mu_N} + {1\over \mu_Z} $$ (2.18)

В данном параграфе отсчет энергии ведется от энергии покоя ядер, которая в отсутствии ядерных превращений остается неизменной.

Рассмотрим предельные случаи формул (2.9).

а) Сильное вырождение. При нулевой температуре электроны заполняют фазовое пространство вплоть до граничного импульса Ферми \( p_{Fe} \). Плотность электронов равна удвоенному (за счет статистического веса) числу ячеек в сферической области фазового пространства радиусом \( p_{Fe} \):


$$ %\begin{displaymath}n_{e}=\frac{2}{\left( 2\pi \hbar \right) ^{3}}\frac{4\pi }{3}p^{3}_{Fe}=\frac{p^{3}_{Fe}}{3\pi ^{2}\hbar ^{3}} \end{displaymath} n_{\mathrm{e}}={2\over (2\pi\hbar)^3} {4\pi\over 3} \pFe^3 = {\pFe^3\over 3\pi^2\hbar^3}. $$ (2.19)

С учетом (2.17) получаем в отсутствие позитронов


$$ %\begin{displaymath} %p_{Fe}=\left( \frac{3\pi ^{2}\rho }{\mu _{Z}m_{u}}\right) ^{1/3} , \quad %\hbar =\left( \frac{1.027\rho }{10^{6}\mu _{Z}}\right) ^{1/3}m_{e}c . %\end{displaymath} \pFe=\left(3\pi^2\rho\over \mu_Z m_{\mathrm{u}}\right)^{1/3} \hbar=\left(1.027\rho\over 10^6\mu_Z\right)^{1/3}\mec{}{}. $$ (2.20)

Кинетическая энергия электрона на границе фазовой области называется энергией Ферми:


$$ %\begin{displaymath} %\hbox{% %\begin{tabular}{l} %$\displaystyle{ \epsilon _{Fe}=\left( m_{e}^{2}c^{4}+p_{Fe}^{2}c^{2}\right) ^{1/2}-m_{e}c^{2}=m_{e}c^{2}\left( \sqrt{1+y^{2}}-1\right) , \quad % y=\frac{p_{Fe}}{m_{e}c} , }$ %$\displaystyle{ \rho =\frac{m_{e}^{3}c^3\mu_Z m_u}{3\pi^2\hbar^3}y^3 =9.740\cdot10^5 \mu_Z \left[\left(\frac{\epsilon_{Fe}}{m_ec^2}+1\right)^2-1\right]^{3/2} . }$ %\end{tabular}} %\end{displaymath} \eqalign{ &\eFe=(\mec24+\pFe^2 c^2)^{1/2}-\mec{}2=\mec{}2(\rady{}-1), \cr \noalign{\medskip} &y={\pFe\over \mec{}{}}, \cr &\rho={\mec33 \mu_Z m_{\mathrm{u}}\over 3\pi^2\hbar^3} y^3= 9.740\cdot10^5\mu_Z\left[\left({\eFe\over \mec{}2}+ 1\right)^2-1\right]^{3/2}. \cr} $$ (2.21)

Учтя, что \( f_{e}=1 \) при \( p\lt p_{Fe} \) и \( f_{e}=0 \) при \( p\gt p_{Fe} \), получаем из (2.5), (2.6)


$$ %\begin{displaymath} %\hbox{% %\begin{tabular}{l} %$\displaystyle{ E_{e}=\frac{2}{\rho }\frac{4\pi }{(2\pi \hbar )^{3}}\int ^{p_{Fe}}_{0}(p^{2}c^{2}+m^{2}_{e}c^{4})^{1/2}p^{2}dp=\frac{m^{4}_{e}c^{5}}{24\pi ^{2}\hbar ^{3}\rho }g(y)= }$ [3mm] %$\displaystyle{ \qquad =\frac{6.002\cdot 10^{22}}{\rho }g(y) , }$ [3mm] %$\displaystyle{ P_{e}=\frac{2}{3}\frac{4\pi c}{(2\pi \hbar )^{3}}\int ^{p_{Fe}}_{0}(p^{2}+m^{2}_{e}c^{4})^{-1/2}p^{4}dp=\frac{m^{4}_{e}c^{5}}{24\pi ^{2}\hbar ^{3}}f(y) , }$ %\end{tabular}} %\end{displaymath} \eqalign{ &\eqalign{ E_{\mathrm{e}}&={2\over \rho}\pipih\int_0^{\pFe} (p^2 c^2+\mec24)^{1/2}p^2 dp\cr &=\mcpih{24}\rho g(y)={6.002\cdot 10^{22}\over \rho} g(y),\cr }\cr &P_{\mathrm{e}}={2\over 3}{4\pi c\over (2\pi\hbar)^3}\int_0^{\pFe} (p^2+\mec22)^{-1/2}p^4 dp=\mcpih{24}{}f(y),\cr } $$ (2.22)

где


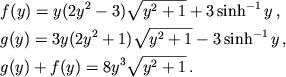\begin{displaymath} \eqalign{ & f(y)=y(2y^{2}-3)\sqrt{y^{2}+1}+3 \sinh^{-1} y\,, \cr & g(y)=3y(2y^{2}+1)\sqrt{y^{2}+1}-3 \sinh^{-1} y\,, \cr & g(y)+f(y)=8y^{3}\sqrt{y^{2}+1}\,. \cr } \end{displaymath} (2.23)

Температурные поправки при сильном вырождении находятся из разложения общих формул с помощью соотношения [145]


$$ %\begin{displaymath}\int _{0}^{\infty }\frac{\varphi (u)du}{e^{^{u-u_{0}}}+1}=\int _{0}^{u_{0}}\varphi (u)du+\frac{\pi ^{2}}{6}\varphi '(u_{0})+\frac{7\pi ^{4}}{360}\varphi (2.24)

которое справедливо при \( e^{^{_{-u_{0}}}}\ll 1 \). Обозначая \( u=\sqrt{x^{2}+\alpha ^{2}}-\alpha \), \( u_{0}=\beta -\alpha \) и пренебрегая вкладом позитронов \( e^{-u_{0}} \), получаем [166] из (2.9), (2.10)


\begin{displaymath}n_{e}=\frac{1}{3\pi ^{2}}\left( \frac{\mec{}{}}{\hbar }\right) ^{3}\left[ y^{3}_{1}+\piay{}2{}21{}\left( y^{2}_{1}+\frac{1}{2}\right) +\piay74{40}415+\ldots\right] , \end{displaymath} (2.25)


\begin{displaymath} \eqalign{ E_{\mathrm{e}}=&\mcpih{24}\rho \Biggl[g(y_1)+\piay42{}21{}(3y_1^2+1)\rady1 \cr &\qquad+\piay745415 (2y_1^4-y_1^2+1)\rady1+\ldots\Biggr], \cr } \end{displaymath} (2.26)


\begin{displaymath} \eqalign{ P_{\mathrm{e}}=\mcpih{24}{} &\Biggl[f(y_1)+{4\pi^2\over \alpha^2}y_1\rady1 \cr &\qquad+\piay74{15}413 (2y_1^2-1)\rady1+\ldots\Biggr], \cr } \end{displaymath} (2.27)


\begin{displaymath} \eqalign{ S_{\mathrm{e}}={\mec2{}\over 3\hbar^3\rho}k^2T &\Biggl[y_1\rady1 \cr &\qquad+\piay72{15}213(y_1^2-{1\over 2})\rady1+\ldots\Biggr]. \cr } \end{displaymath} (2.28)

Здесь \( y_{1}=\sqrt{\beta ^{2}-\alpha ^{2}}/\alpha \), параметр разложения \( \alpha y_{1}\gg 1 \), а функции \( \varphi (u) \) после сведения интегралов (2.10) к виду (2.24) равны \( \varphi _{n}=(u+\alpha )\sqrt{u^{2}+2u\alpha } \), \( \varphi _{E}=(u+\alpha )^{2}\sqrt{u^{2}+2u\alpha } \), \( \varphi _{P}=(u^{2}+2u\alpha )^{3/2} \). Найдем явную зависимость \( E_{e} \), \( P_{e} \) и \( S_{e} \) от \( \rho \) и \( T \), оставляя только члены ~\( \alpha ^{-2} \). Используя определение \( y \) из (2.20), (2.21) и соотношение (2.25), получаем связь между \( y \), \( y_{1} \) и \( \alpha \):


$$ %\begin{displaymath} %y=\left( \frac{3\pi ^{2}\rho }{\mu _{Z}\mu _{u}}\right) ^{1/3}\frac{\hbar }{m_{e}c} , \quad %y^{3}=y^{3}_{1}+\frac{\pi ^{2}}{\alpha ^{2}y_{1}}\left( y^{2}_{1}+\frac{1}{2}\right) . %\end{displaymath} y=\left(3\pi^2\rho\over \mu_Z m_{\mathrm{u}} \right)^{1/3}{\hbar\over\mec{}{}},\quad y^3=y_1^3+\piay{}2{}21{}\left(y_1^2+{1\over 2}\right) $$ (2.29)

Учтя малость \( (y^{3}-y^{3}_{1}) \), получим


$$ %\begin{displaymath}y^{3}_{1}=y^{3}-\frac{\pi ^{2}}{\alpha ^{2}y}\left( y^{2}+\frac{1}{2}\right) . \end{displaymath} y_1^3=y^3-\piay{}2{}2{}{}\left(y^2+{1\over 2}\right). $$

После подстановки \( y_{1}(y) \) в (2.23), (2.25)-(2.28) имеем


$$ %\begin{displaymath}g(y_{1})=g(y)-\frac{8\pi ^{2}}{\alpha ^{2}y}\left( y^{2}+\frac{1}{2}\right) \sqrt{y^{2}+1} , \end{displaymath} g(y_1)=g(y)-\piay82{}2{}{}\left(y^2+{1\over 2}\right)\rady{} $$


$$ %\begin{displaymath}f(y_{1})=f(y)-\frac{8\pi ^{2}}{3\alpha ^{2}}\left( y^{2}+\frac{1}{2}\right) \frac{y}{\sqrt{y^{2}+1}} \end{displaymath} f(y_1)=f(y)-{8\pi^2\over 3\alpha^2}\left(y^2+{1\over 2}\right) {y\over \rady{}} $$

и явные выражения термодинамических функций


$$ %\begin{displaymath} %\hbox{% %\begin{tabular}{l} %$\displaystyle{ E_{e}=\frac{m^{4}_{e}c^{5}}{24\pi ^{2}\hbar ^{3}\rho }\left[ g(y)+\frac{4\pi ^{2}}{\alpha ^{2}}y\sqrt{y^{2}+1}\right] , }$ [3mm] %$\displaystyle{ P_{e}=\frac{m^{4}_{e}c^{5}}{24\pi ^{2}\hbar ^{3}\rho }\left[ f(y)+\frac{4\pi ^{2}}{3\alpha ^{2}}y\frac{y^{2+2}}{\sqrt{y^{2}+1}}\right] , }$ [3mm] %$\displaystyle{ S_{e}=\frac{m^{2}_{e}c1}{3\hbar ^{3}\rho }k^{2}Ty\sqrt{y^{2}+1} }$ %\end{tabular}} %\end{displaymath} \eqalign{ &E_{\mathrm{e}}=\mcpih{24}\rho\left[g(y)+{4\pi^2\over \alpha^2}y\rady{}\right], \cr \noalign{\smallskip} &P_{\mathrm{e}}=\mcpih{24}{}\left[f(y)+{4\pi^2\over 3\alpha^2} y{y^2+2\over \rady{}}\right], \cr &S_{\mathrm{e}}={\mec2{}\over 3\hbar^3\rho} k^2Ty\rady{}. \cr } $$ (2.30)

В предельных случаях функции \( f \) и \( g \) равны


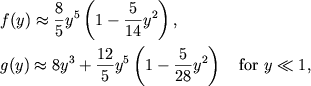$$ %\begin{displaymath} %f(y)\approx \frac{8}{5}y^{5}\left( 1-\frac{5}{14}y^{2}\right) , \quad %g(y)\approx 8y^{3}+\frac{12}{5}y^{5}\left( 1-\frac{5}{28}y^{2}\right) %\mbox{~при~} y\ll 1 , %\end{displaymath} \eqalign{ &f(y)\approx{8\over 5}y^5\left(1-{5\over 14}y^2\right), \cr &g(y)\approx 8y^3+{12\over 5}y^5\left(1-{5\over 28}y^2\right)\quad \hbox{\rm for } y\ll 1, \cr } $$ (2.31)

и

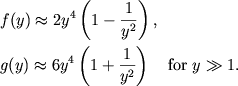
$$ %\begin{displaymath} %f(y)\approx 2y^{4}\left( 1-\frac{1}{y^{2}}\right) , \quad %g(y)\approx 6y^{4}\left( 1+\frac{1}{y^{2}}\right) %\mbox{~при~} y \gg 1 . %\end{displaymath} \eqalign{ &f(y)\approx 2y^4\left(1-{1\over y^2}\right), \cr &g(y)\approx 6y^4\left(1+{1\over y^2}\right)\quad \hbox {\rm for } y \gg 1. \cr } $$

Учтя (2.31), в нерелятивистском пределе \( y\ll 1 \) получаем из (2.30)


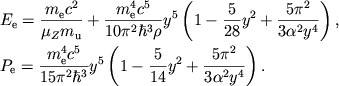$$ %\begin{displaymath} %\hbox{% %\begin{tabular}{l} %$\displaystyle{ E_{e}=\frac{m_{e}c^{2}}{\mu _{Z}m_{u}}+\frac{m^{4}_{e}c^{5}}{10\pi ^{2}\hbar ^{3}\rho }y^{5}\left( 1-\frac{5}{28}y^{2}+\frac{5\pi ^{2}}{3\alpha ^{2}y^{4}}\right) , }$ %$\displaystyle{ P_{e}=\frac{m^{4}_{e}c^{5}}{15\hbar ^{3}\pi ^{2}}y^{5}\left( 1-\frac{5}{14}y^{2}+\frac{5\pi ^{2}}{3\alpha ^{2}y^{4}}\right) . }$ %\end{tabular}} %\end{displaymath} \eqalign{ &E_{\mathrm{e}}={\mec{}2\over \mu_Z m_{\mathrm{u}}}+\mcpih{10}\rho y^5 \left(1-{5\over 28}y^2+\piay5232{}4 \right), \cr &P_{\mathrm{e}}=\mcpih{15}{} y^5 \left(1-{5\over 14}y^2+\piay5232{}4 \right). \cr } $$ (2.32)

В ультрарелятивистском пределе \( y\gg 1 \) соответственно имеем


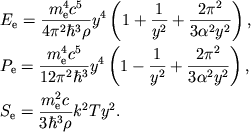$$ %\begin{displaymath} %\hbox{% %\begin{tabular}{l} %$\displaystyle{ E_{e}=\frac{m^{4}_{e}c^{5}}{4\pi ^{2}\hbar ^{3}\rho }y^{4}\left( 1+\frac{1}{y^{2}}+\frac{2\pi ^{2}}{3\alpha ^{2}y^{2}}\right) , }$ %$\displaystyle{ P_{e}=\frac{m^{4}_{e}c^{5}}{12\pi ^{2}\hbar ^{3}}y^{4}\left( 1-\frac{1}{y^{2}}+\frac{2\pi ^{2}}{3\alpha ^{2}y^{2}}\right) , }$ %$\displaystyle{ S_{e}=\frac{m^{2}_{e}c}{3\hbar ^{3}\rho }k^{2}Ty^{2} . }$ %\end{tabular}} %\end{displaymath} \eqalign{ &E_{\mathrm{e}}=\mcpih{4}\rho y^4 \left(1+{1\over y^2}+\piay2232{}2 \right), \cr &P_{\mathrm{e}}=\mcpih{12}{} y^4 \left(1-{1\over y^2}+\piay2232{}2 \right), \cr &S_{\mathrm{e}}={\mec2{}\over 3\hbar^3\rho} k^2Ty^2. \cr } $$ (2.33)

б) Очень малая плотность вещества. Плотность вещества может быть настолько малой, что концентрация пар превысит концентрацию исходных электронов. В этом случае малым параметром является величина \( \beta \ll 1 \); при \( \beta =0 \) имеет место \( n_{e}=n_{e+} \). Разлагая (2.10) в ряд по \( \beta \), получим, используя интегрирование по частям,


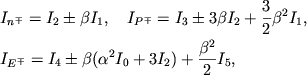$$ %\begin{displaymath} %\hbox{% %\begin{tabular}{ll} %$\displaystyle{ I_{n\mp }=I_{2}\pm \beta I_{1} , \qquad I_{p\mp }=I_{3}\pm \beta I_{2}+\frac{3}{2}\beta ^{2}I_{1} , }$ %$\displaystyle{ I_{E\mp }=I_{4}\pm \beta \left( \alpha ^{2}I_{0}+3I_{2}\right) +\frac{\beta ^{2}}{2}I_{5} , }$ %\end{tabular}} %\end{displaymath} \eqalign{ &\Imp{n}=I_2\pm \beta I_1,\quad \Imp{P}=I_3\pm 3\beta I_2+{3\over 2}\beta^2 I_1, \cr &\Imp{E}=I_4\pm \beta(\alpha^2 I_0+3I_2)+{\beta^2\over 2}I_5, \cr } $$ (2.34)

где
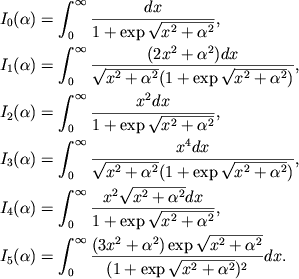$$ %\begin{displaymath} %\hbox{% %\begin{tabular}{l} %$\displaystyle{ I_{0}(\alpha )=\int _{0}^{\infty }\frac{dx}{1+\exp \sqrt{x^{2}+\alpha ^{2}}}_{0} , }$ %$\displaystyle{ I_{1}(\alpha )=\int _{0}^{\infty }\frac{(2x^{2}+\alpha ^{2})dx}{\sqrt{x^{2}+\alpha ^{2}}\left( 1+\exp \sqrt{x^{2}+\alpha ^{2}}\right) } , }$ %$\displaystyle{ I_{2}(\alpha )=\int _{0}^{\infty }\frac{x^{2}dx}{1+\exp \sqrt{x^{2}+\alpha ^{2}}} , }$ %$\displaystyle{ I_{3}(\alpha )=\int _{0}^{\infty }\frac{x^{4}dx}{\sqrt{x^{2}+\alpha ^{2}}\left( 1+\exp \sqrt{x^{2}+\alpha ^{2}}\right) } , }$ %$\displaystyle{ I_{4}(\alpha )=\int _{0}^{\infty }\frac{x^{2}\sqrt{x^{2}+\alpha ^{2}}dx}{1+\exp \sqrt{x^{2}+\alpha ^{2}}} , }$ %$\displaystyle{ I_{5}(\alpha )=\int _{0}^{\infty }\frac{(3x^{2}+\alpha ^{2})\exp \sqrt{x^{2}+\alpha ^{2}}}{\left( 1+\exp \sqrt{x^{2}+\alpha ^{2}}\right) ^{2}}dx . }$ %\end{tabular}} %\end{displaymath} \eqalign{ &\Ia0=\intinf{dx\over \eradxa}, \cr &\Ia1=\intinf{(2x^2+\alpha^2)dx\over \radxa(\eradxa)}, \cr &\Ia2=\intinf{x^2dx\over \eradxa}, \cr &\Ia3=\intinf{x^4dx\over \radxa (\eradxa)}, \cr &\Ia4=\intinf{x^2\radxa dx\over \eradxa}, \cr &\Ia5=\intinf{(3x^2+\alpha^2)\exp\radxa\over (\eradxa)^2}dx. \cr } $$ (2.35)

При \( \alpha =0 \) интегралы (2.35) выражаются [145] через $\Gamma$-функцию и $\zeta$-функцию Римана с помощью соотношения

$$ %\begin{displaymath} %F_{\nu }(0)=\int ^{\infty }_{0}\frac{x^{\nu -1}dx}{1+e^{x}}=(1-2^{1-\nu })\Gamma(\nu )\zeta (\nu ) , %\quad \nu \gt 0 %\end{displaymath} F_\nu(0)=\intinf{x^{\nu-1}dx\over 1+e^x}= (1-2^{1-\nu})\Gamma(\nu)\zeta(\nu), \quad \nu>0 $$ (2.36)

и формулы

$$ %\begin{displaymath}\int ^{\infty }_{0}\frac{dx}{1+e^{x}}=\ln 2 . \end{displaymath} \intinf{dx\over 1+e^x}=\ln 2. $$

Учитывая для целых \( \nu =n \) значения \( \zeta (n) \) из [145] и \( \Gamma(n)=(n-1)! \), получаем

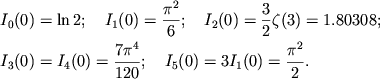$$ %\begin{displaymath} %\hbox{% %\begin{tabular}{l} %$\displaystyle{ I_{0}(0)=\ln 2 ; \quad I_{1}(0)=\frac{\pi ^{2}}{6} ; \quad I_{2}(0)=\frac{3}{2}\zeta (3)=1.80308 ; }$ %$\displaystyle{ I_{3}(0)=I_{4}(0)=\frac{7\pi ^{4}}{120} ; \quad I_{5}(0)=3I_{1}(0)=\pi ^{2}/2 . }$ %\end{tabular}} %\end{displaymath} \eqalign{ &I_0(0)=\ln 2;\quad I_1(0)={\pi^2\over 6};\quad I_2(0)={3\over 2}\zeta(3)=1.80308; \cr &I_3(0)=I_4(0)={7\pi^4\over 120};\quad I_5(0)=3I_1(0)={\pi^2\over 2}. \cr } $$ (2.37)

С учетом (2.34)-(2.37) и определения \( y \) в (2.29), термодинамические функции с учетом (2.9), (2.17) примут вид

$$ %\begin{displaymath} %\hbox{% %\begin{tabular}{l} %$\displaystyle{ \beta =\frac{y^{3}\alpha ^{3}}{\pi ^{2}A_{2}} , \quad n_{e\mp}=\frac{15}{\pi ^{4}}I_{2}(0)\frac{aT^{3}}{k}A_{1}\left( 1\pm \frac{1}{6I_{2}(0)}\frac{y^{3}\alpha ^{3}}{A_{1}}\right) , }$ [3mm] %$\displaystyle{ E_{e-}+E_{e+}=\frac{7}{4}\frac{aT^{4}}{\rho }B_{0}\left( 1+\frac{30}{7\pi ^{6}}\frac{B_{2}}{B_{0}A^{2}_{2}}y^{6}\alpha ^{6}\right) , }$ [3mm] %$\displaystyle{ P_{e-}+P_{e+}=\frac{7}{12}aT^{4}A_{0}\left( 1+\frac{30}{7\pi ^{6}}\frac{y^{6}\alpha ^{6}}{A_{0}A_{2}}\right) , }$ [3mm] %$\displaystyle{ S_{e-}+S_{e+}=\frac{7}{3}\frac{aT^{3}}{\rho }\frac{3B_{0}+A_{0}}{4}\left( 1+\frac{15}{7\pi ^{6}}\frac{6B_{2}-2A_{2}}{3B_{0}+A_{0}}\frac{y^{6}\alpha ^{6}}{A^{2}_{2}}\right) , }$ %\end{tabular}} %\end{displaymath} \eqalign{ &\beta={\ya3\over \pi^2 A_2},\quad n_{\mathrm{e^\mp}}={15\over \pi^4}I_2(0){\alpha T^3\over k}A_1 \left(1\pm {1\over 6I_2(0)}{\ya3\over A_1}\right), \cr \noalign{\smallskip} &E_{\mathrm{e^-}}+E_{\mathrm{e^+}}={7\over 4}{\alpha T^4\over \rho}B_0 \left(1+ {30\over 7\pi^6}{B_2\over B_0 A_2^2}\ya6\right), \cr \noalign{\smallskip} &P_{\mathrm{e^-}}+P_{\mathrm{e^+}}={7\over 12}\alpha T^4 A_0 \left(1+ {30\over 7\pi^6}{\ya6\over A_0 A_2}\right), \cr \noalign{\smallskip} &S_{\mathrm{e^-}}+S_{\mathrm{e^+}}={7\over 3}{\alpha T^3\over \rho}{3B_0+A_0\over 4} \left(1+ {15\over 7\pi^6}{6B_2-2A_2\over 3B_0+A_0} {y^6a^6\over A_2^2}\right), \cr } $$ (2.38)

где введены функции
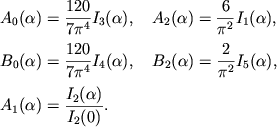$$ %\begin{displaymath} %\hbox{% %\begin{tabular}{l} %$\displaystyle{ A_{0}(\alpha )=\frac{120}{7\pi ^{4}}I_{3}(\alpha ) , \quad A_{2}(\alpha )=\frac{6}{\pi ^{2}}I_{1}(\alpha ) , }$ %$\displaystyle{ B_{0}(\alpha )=\frac{120}{7\pi ^{4}}I_{4}(\alpha ) , \quad B_{2}(\alpha )=\frac{2}{\pi ^{2}}I_{5}(\alpha ) , }$ %$\displaystyle{ A_{1}(\alpha )=\frac{I_{2}(\alpha )}{I_{2}(0)} . }$ %\end{tabular}} %\end{displaymath} \eqalign{ &A_0(\alpha)={120\over 7\pi^4}\Ia3, \quad A_2(\alpha)={6\over \pi^2}\Ia1, \cr \noalign{\smallskip} &B_0(\alpha)={120\over 7\pi^4}\Ia4, \quad B_2(\alpha)={2\over \pi^2}\Ia5, \cr \noalign{\smallskip} &A_1(\alpha)={\Ia2\over I_2(0)}. \cr } $$ (2.39)

В случае ультрарелятивистских пар \( \alpha \ll 1 \) для (2.39) имеют место асимптотические представления [166]

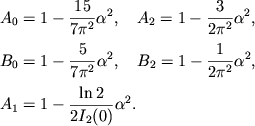$$ %\begin{displaymath} %\hbox{% %\begin{tabular}{l} %$\displaystyle{ A_{0}=1-\frac{15}{7\pi ^{2}}\alpha ^{2} , \quad A_{2}=1-\frac{3}{2\pi ^{2}}\alpha ^{2} , }$ %$\displaystyle{ B_{0}=1-\frac{5}{7\pi ^{2}}\alpha ^{2} , \quad B_{2}=1-\frac{1}{2\pi ^{2}}\alpha ^{2} , }$ %$\displaystyle{ A_{1}=1-\frac{\ln 2}{2I_{2}(0)}\alpha ^{2} . }$ %\end{tabular}} %\end{displaymath} \eqalign{ &A_0=1-{15\over 7\pi^2}\alpha^2,\quad A_2=1-{3\over 2\pi^2}\alpha^2, \cr \noalign{\smallskip} &B_0=1-{5\over 7\pi^2}\alpha^2,\quad B_2=1-{1\over 2\pi^2}\alpha^2, \cr \noalign{\smallskip} &A_1=1-{\ln2\over 2I_2(0)}\alpha^2. \cr } $$ (2.40)

Из (2.38)-(2.40) получаем термодинамические функции вблизи ультрарелятивистских пар в газе малой плотности

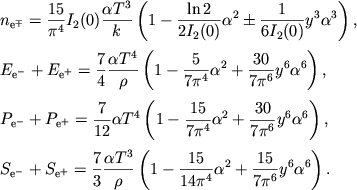$$ \eqalign{ & n_{\mathrm{e^\mp}}={15\over \pi^4}I_2(0){\alpha T^3\over k} \left(1-{\ln 2\over 2I_2(0)}\alpha^2\pm{1\over 6I_2(0)}\ya3\right), \cr \noalign{\smallskip} & E_{\mathrm{e^-}}+E_{\mathrm{e^+}}={7\over 4}{\alpha T^4\over \rho} \left(1-{5\over 7\pi^4}\alpha^2+{30\over 7\pi^6}\ya6\right), \cr \noalign{\smallskip} & P_{\mathrm{e^-}}+P_{\mathrm{e^+}}={7\over 12}\alpha T^4 \left(1-{15\over 7\pi^4}\alpha^2+{30\over 7\pi^6}\ya6\right), \cr \noalign{\smallskip} & S_{\mathrm{e^-}}+S_{\mathrm{e^+}}={7\over 3}{\alpha T^3\over \rho} \left(1-{15\over 14\pi^4}\alpha^2+{15\over 7\pi^6}\ya6\right). \cr } $$ (2.41)

В нерелятивистском пределе \( \alpha \gg 1 \), оставляя два члена при разложении знаменателя в (2.35), имеем [93]

$$ %\begin{displaymath} %\hbox{% %\begin{tabular}{l} %$\displaystyle{ A_{0}=\frac{360}{7\pi ^{4}}\alpha ^{2}\left[ K_{2}(\alpha )-\frac{1}{4}K_{2}(2\alpha )\right] , }$ %$\displaystyle{ B_{0}=\frac{120}{7\pi ^{4}}\alpha ^{2}\left[ \alpha K_{1}(\alpha )+3K_{2}(\alpha )-\frac{\alpha }{2}K_{1}(2\alpha )-\frac{3}{4}K_{2}(2\alpha )\right] , }$ %$\displaystyle{ A_{1}=\frac{\alpha ^{2}}{I_{2}(0)}\left[ K_{2}(\alpha )-\frac{1}{2}K_{2}(2\alpha )\right] , }$ %$\displaystyle{ A_{2}=\frac{6\alpha ^{2}}{\pi ^{4}}\left[ K_{2}(\alpha )-K_{2}(2\alpha )\right] , }$ %$\displaystyle{ B_{2}=\frac{2\alpha ^{2}}{\pi ^{2}}\left[ \alpha K_{1}(\alpha )+3K_{2}(\alpha )-2\alpha K_{1}(2\alpha )-3K_{2}(2\alpha )\right] . }$ %\end{tabular}} %\end{displaymath} \eqalign{ &A_0={360\over 7\pi^4}\alpha^2 \left[\Ka2{}-{1\over 4}\Ka22\right], \cr \noalign{\smallskip} &B_0={120\over 7\pi^4}\alpha^2 \left[\alpha \Ka1{}+3\Ka2{}-{\alpha\over 2}\Ka12-{3\over 4}\Ka22\right], \cr \noalign{\smallskip} &A_1={\alpha^2\over I_2(0)}\left[\Ka2{}-{1\over 2}\Ka22\right],\quad A_2={6\alpha^2\over \pi^4}\left[\Ka2{}-\Ka22\right], \cr \noalign{\smallskip} &B_2={2\alpha^2\over \pi^2} \left[\alpha \Ka1{}+3\Ka2{}-2\alpha \Ka12-3\Ka22\right], \cr } $$ (2.42)

где \( K_{n}(\alpha ) \) - функции Бесселя мнимого агрумента (Ганкеля), имеющие разложения при \( \alpha \gg 1 \) [93]:
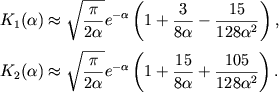$$ %\begin{displaymath} %\hbox{% %\begin{tabular}{l} %$\displaystyle{ K_{1}(\alpha )\approx \sqrt{\frac{\pi }{2\alpha }}e^{-\alpha }\left( 1+\frac{3}{8\alpha }-\frac{15}{128\alpha ^{2}}\right) , }$ %$\displaystyle{ K_{2}(\alpha )\approx \sqrt{\frac{\pi }{2\alpha }}e^{-\alpha }\left( 1+\frac{15}{8\alpha }+\frac{105}{128\alpha ^{2}}\right) . }$ %\end{tabular}} %\end{displaymath} \eqalign{ &\Ka1{}\approx \sqrt{{\pi\over 2\alpha}}e^{-\alpha} \left(1+{3\over 8\alpha}-{15\over 128\alpha^2}\right), \cr \noalign{\smallskip} &\Ka2{}\approx \sqrt{{\pi\over 2\alpha}}e^{-\alpha} \left(1+{15\over 8\alpha}+{105\over 128\alpha^2}\right). \cr } $$ (2.43)

В табл. 3 приведены значения функций $A_{i}(\alpha )$, $B_{i}(\alpha )$ для $0\leq \alpha \leq 10$, полученные численным интегрированием в [167].

в) Слабое вырождение. Слабое вырождение соответствует \( f_{e}\ll 1 \) в (2.2). Тогда в интегралах (2.10) можно провести разложение в ряд, воспользовавшись большим значением экспоненты в знаменателе. Оставляя два первых члена разложения, получаем [218, 166, 363, 93]

$$ %\begin{displaymath} %\hbox{% %\begin{tabular}{l} %$\displaystyle{ I_{n\mp }=\alpha ^{2}\left[ K_{2}(\alpha )e^{\pm \beta }-\frac{1}{2}K_{2}(2\alpha )e^{\pm 2\beta }\right] , }$ %$\displaystyle{ I_{P\mp }=3\alpha ^{2}\left[ K_{2}(\alpha )e^{\pm \beta }-\frac{1}{4}K_{2}(2\alpha )e^{\pm 2\beta }\right] , }$ %$\displaystyle{ I_{E\mp }=\alpha ^{3}\left[ K_{1}(\alpha )e^{\pm \beta }+\frac{3}{\alpha }K_{2}(\alpha )e^{\pm \beta }-\frac{1}{2}K_{1}(2\alpha )e^{\pm 2\beta }-\frac{3}{4\alpha }K_{2}(2\alpha )e^{\pm 2\beta }\right] . }$ %\end{tabular}} %\end{displaymath} \eqalign{ &\Imp{n}=\alpha^2\left[\Ka2{}\epmb{}-{1\over 2}\Ka22\epmb2\right], \cr \noalign{\medskip} &\Imp{P}=3\alpha^2\left[\Ka2{}\epmb{}-{1\over 4}\Ka22\epmb2\right], \cr \noalign{\medskip} &\eqalign{ \Imp{E}&=\alpha^3\Biggl[\Ka1{}\epmb{}+{3\over \alpha}\Ka2{}\epmb{} \cr &\qquad-{1\over 2}\Ka12\epmb2-{3\over 4\alpha}\Ka22\epmb2\Biggr]. \cr }\cr } $$ (2.44)


Таблица 3. Значение функций $A_{i}(\alpha )$, $B_{i}(\alpha )$ для $0\leq \alpha \leq 10$.
\( \alpha \) \( A_{0} \) \( A_{1} \) \( A_{2} \) \( B_{0} \) \( B_{1} \) \( B_{2} \)
0.00 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000
0.50 9.4989 (-1) 9.5476 (-1) 9.6299 (-1) 9.8119 (-1) 9.8342 (-1) 9.8702 (-1)
1.00 8.2749 (-1) 8.4020 (-1) 8.6278 (-1) 9.2303 (-1) 9.3130 (-1) 9.4529 (-1)
1.50 6.7622 (-1) 6.9345 (-1) 7.2532 (-1) 8.3028 (-1) 8.4519 (-1) 8.7168 (-1)
2.00 5.2709 (-1) 5.4480 (-1) 5.7846 (-1) 7.1580 (-1) 7.3497 (-1) 7.7039 (-1)
2.50 3.9653 (-1) 4.1217 (-1) 4.4246 (-1) 5.9438 (-1) 6.1464 (-1) 6.5311 (-1)
3.00 2.9030 (-1) 3.0290 (-1) 3.2762 (-1) 4.7800 (-1) 4.9689 (-1) 5.3345 (-1)
3.50 2.0806 (-1) 2.1764 (-1) 2.3656 (-1) 3.7418 (-1) 3.9040 (-1) 4.2216 (-1)
4.00 1.4664 (-1) 1.5360 (-1) 1.6748 (-1) 2.8635 (-1) 2.9949 (-1) 3.2544 (-1)
4.50 1.0189 (-1) 1.0685 (-1) 1.1675 (-1) 2.1497 (-1) 2.2520 (-1) 2.4549 (-1)
5.00 7.0003 (-2) 7.3461 (-2) 8.0361 (-2) 1.5877 (-1) 1.6650(-1) 1.8188 (-1)
5.50 4.7634 (-2) 5.0006 (-2) 5.4746 (-2) 1.1563 (-1) 1.2133 (-1) 1.3271 (-1)
6.00 3.2147 (-2) 3.3756 (-2) 3.6973 (-2) 8.3190 (-2) 8.7329 (-2) 9.5597 (-2)
7.00 1.4345 (-2) 1.5066 (-2) 1.6510 (-2) 4.1752 (-2) 4.3848 (-2) 4.8039 (-2)
8.00 6.2613 (-3) 6.5769 (-3) 7.2085 (-3) 2.0259 (-2) 2.1280 (-2) 2.3321 (-2)
9.00 2.6856 (-3) 2.8211 (-3) 3.0922 (-3) 9.5667 (-3) 1.0049 (-2) 1.1014 (-2)
10.0 1.1356 (-3) 1.1929 (-3) 1.3076 (-3) 4.4175 (-3) 4.6404 (-3) 5.0864 (-3)
В данной и последующих таблицах в скобках указан порядок величины

Из (2.17) имеем с нужной точностью, учтя (2.44) и величину \( y \) из (2.29),2

$$ %\begin{displaymath} %\hbox{% %\begin{tabular}{l} %$\displaystyle{ \sh\beta = \frac{\alpha y^3}{6K_2(\alpha)} \left[1 + \frac{K_2(2\alpha)}{K_2(\alpha)}\sqrt{1+\frac{\alpha^2y^6}{36K_2^2(\alpha)} } \right] , }$ %$\displaystyle{ \ch\beta = \sqrt{1+\frac{\alpha^2y^6}{36K_2^2(\alpha)} } + \frac{K_2(2\alpha)}{K_2(\alpha)} \frac{\alpha^2y^6}{36K_2^2(\alpha)} , }$ %$\displaystyle{ \ch 2\beta = 1 + 2\frac{\alpha^2y^6}{36K_2^2(\alpha)} , \quad % \sh 2\beta = \frac{\alpha y^3}{3K_2(\alpha)} \sqrt{1+\frac{\alpha^2y^6}{36K_2^2(\alpha)}} , }$ %$\displaystyle{ \beta = \ln\left[ \frac{\alpha y^3}{6K_2(\alpha)} + \sqrt{1+\frac{\alpha^2y^6}{36K_2^2(\alpha)}} \right] + \frac{K_2(2\alpha)}{K_2(\alpha)} \frac{\alpha y^3}{6K_2(\alpha)} . }$ %\end{tabular}} %\end{displaymath} \eqalign{ &\sinh\beta={\alpha y^3\over 6\Ka2{}}\left[1+{\Ka22\over \Ka2{}} \sqrt{1+\ayka}\>\right], \cr \noalign{\smallskip} &\cosh\beta=\sqrt{1+\ayka}+{\Ka22\over \Ka2{}}\ayka, \cr \noalign{\smallskip} &\cosh 2\beta=1+2\ayka,\quad \sinh 2\beta={\alpha y^3\over 3\Ka2{}}\sqrt{1+\ayka}, \cr \noalign{\smallskip} &\beta=\ln\left[{\alpha y^3\over 6\Ka2{}}+\sqrt{1+\ayka}\>\right]+ {\Ka22\over \Ka2{}}{\alpha y^3\over 6\Ka2{}} \cr}. $$ (2.45)

При выводе (2.45) использовалась малость членов, содержащих , которые учитывают слабое вырождение. С помощью (2.44), (2.45) получаем из (2.9)


$$ %\begin{displaymath} %\ldots S_{e-}+S_{e+}=\frac{6k}{\mu _{Z}m_{u}y^{3}}\left\{ \left[ K_{1}(\alpha )+\frac{4}{\alpha }K_{2}(\alpha )\right] \sqrt{1+\frac{\alpha ^{2}y^{6}}{36K^{2}_{2}(\alpha )}}-\frac{y^{3}}{6}\ln\left[ \frac{\alpha y^{3}}{6K_{2}(\alpha )}+\sqrt{1+\frac{\alpha ^{2}y^{6}}{36K^{2}_{2}(\alpha )}}\right] +\right\} . %\end{displaymath} \eqalign{ &\summp{n}={6\rho\over \muzmu y^3}\left[{\Ka2{}\over \alpha} \sqrt{1+\ayka}-{\Ka22\over 2\alpha}\right], \cr \noalign{\smallskip} &\eqalign{ \summp{E}&={6kT\over \muzmu y^3}\Biggl\{\left[\Ka1{}+{3\over \alpha} \Ka2{}\right]\sqrt{1+\ayka} \cr &\qquad+\left[{3\over 2\alpha}\Ka22-\Ka12+ {\Ka1{}\Ka22\over \Ka2{}}\right] \cr &\qquad\times\ayka-{1\over 2}\Ka12-{3\over 4\alpha}\Ka22\Biggr\}, \cr }\cr &\eqalign{ \summp{P}&={6\rho kT\over \muzmu y^3}\Biggl[{\Ka2{}\over \alpha} \sqrt{1+\ayka} \cr &+{1\over 2\alpha}\Ka22\ayka-{1\over 4} {\Ka22\over \alpha}\Biggr], \cr }\cr \noalign{\smallskip} &\eqalign{ \summp{S}&={6kT\over \muzmu y^3}\Biggl\{\left[\Ka1{}+{4\over \alpha} \Ka2{}\right]\sqrt{1+\ayka} \cr &-{y^3\over 6}\ln\left[{\alpha y^3\over 6\Ka2{}}+ \sqrt{1+\ayka}\>\right] \cr &+\Biggl[{\Ka22\over \alpha}-\Ka12 +{\Ka1{}\Ka22\over \Ka2{}}\Biggr]\ayka \cr &-{\Ka12\over 2}- {\Ka22\over \alpha}\Biggr\}. \cr }\cr } $$ (2.46)

Формулы (2.46) справедливы для слабо вырожденного газа произвольной плотности, в том числе очень малой, когда число рождающихся пар много больше исходного числа электронов и \( \lambda =\alpha ^{2}y^{6}/36K^{2}_{2}(\alpha )\ll 1 \). Необходимо также, чтобы газ не был релятивистским, так как при \( \alpha \leq 1 \) рождающиеся пары заполняют фазовое пространство даже при очень малой плотности. Таким образом, для применимости (2.46) требуется выполнение условия \( \alpha \gg 1 \), когда справедливо разложение (2.43)3.

При \( \lambda \gg 1 \) из (2.46) и (2.43), оставляя два члена разложения по \( 1/\lambda \), получаем термодинамические функции идеального газа с поправками на вырождение, релятивизм и рождение пар (см. также [166])

$$ %\begin{displaymath} %\hbox{% %\begin{tabular}{l} %$\displaystyle{ n_{e-}+n_{e+}=\frac{\rho }{\mu _{Z}m_{u}}\left\{ 1+\frac{9\pi }{\alpha ^{2}y^{6}}e^{-2\alpha }\left[ 1+\frac{15}{4\alpha }-\frac{\alpha ^{3/2}y^{3}}{6\sqrt{\pi }}\left( 1+\frac{15}{16\alpha }\right) \right] \right\} , }$ %$\displaystyle{ E_{e-}+E_{e+}=\frac{m_{e}c^{2}}{\mu _{Z}m_{u}}+\frac{3}{2}\frac{kT}{\mu _{Z}m_{u}}\left\{ 1+\frac{5}{4\alpha }+\frac{\alpha ^{3/2}y^{3}}{12\sqrt{\pi }}\left( 1-\frac{15}{16\alpha }\right) + \right. }$ %$\displaystyle{ \qquad\qquad \left. +\frac{6\pi }{\alpha ^{2}y^{6}}e^{-2\alpha }\left[ 1+\frac{21}{4\alpha }-\frac{\alpha ^{3/2}y^{3}}{6\sqrt{\pi }}\left( 1+\frac{27}{16\alpha }\right) \right] \right\} , }$ %$\displaystyle{ P_{e-}+P_{e+}=\frac{\rho kT}{\mu _{Z}m_{u}}\left\{ 1+\frac{\alpha ^{3/2}y^{3}}{12\sqrt{\pi }}\left( 1-\frac{45}{16\alpha }\right) + \right. }$ %$\displaystyle{ \qquad\qquad \left. + \frac{9\pi }{\alpha ^{3}y^{6}}e^{-2\alpha }\left[ 1+\frac{15}{4\alpha }-\frac{\alpha ^{3/2}y^{3}}{12\sqrt{\pi }}\left( 1+\frac{15}{16\alpha }\right) \right] \right\} , }$ %$\displaystyle{ S_{e-}+S_{e+}=\frac{k}{\mu _{Z}m_{u}}\left\{ \frac{5}{2}-\ln\left( \sqrt{\frac{2}{\pi }}\frac{\alpha ^{3/2}y^{3}}{3}\right) +\frac{15}{4\alpha }+\frac{\alpha ^{3/2}y^{3}}{24\sqrt{\pi }}\left( 1+\frac{45}{15\alpha }\right) + \right. }$ %$\displaystyle{ \qquad\qquad \left. +\frac{9\pi }{\alpha ^{2}y^{6}}e^{-2\alpha }\left[ 1+\frac{23}{4\alpha }-\frac{\alpha ^{3/2}y^{3}}{6\sqrt{\pi }}\left( 1+\frac{35}{16\alpha }\right) \right] \right\} . }$ %\end{tabular}} %\end{displaymath} \eqalign{ &\eqalign{ \summp{n}&={\rho\over \muzmu}\Biggl\{1+{9\pi\over \alpha^3 y^6} e^{-2\alpha}\Biggl[1+{15\over 4\alpha} \cr &\qquad-\ayspi6\left(1+{15\over 16\alpha} \right)\Biggr]\Biggr\}, \cr }\cr &\eqalign{ \summp{E}&=+{\mec{}2\over \muzmu}+{3\over 2} {kT\over \muzmu}\Biggl\{1+{5\over 4\alpha} \cr &\qquad+\ayspi{12}\left(1-{15\over 16\alpha}\right)+ {6\pi\over \alpha^2 y^6}e^{-2\alpha} \cr &\qquad\times\left[1+{21\over 4\alpha}-\ayspi6 \left(1+{27\over 16\alpha}\right)\right]\Biggr\}, \cr }\cr &\eqalign{ \summp{P}&={\rho kT\over \muzmu}\Biggl\{1+\ayspi{12} \left(1-{45\over 16\alpha}\right) \cr &\qquad+{9\pi\over \alpha^3 y^6}e^{-2\alpha}\left[1+{15\over 4\alpha}- \ayspi{12}\left(1+{15\over 16\alpha}\right)\right]\Biggr\}, \cr }\cr &\eqalign{ \summp{S}&={k\over \muzmu}\Biggl\{ {5\over 2}-\ln\left( \sqrt{{2\over\pi}}{\alpha^{3/2} y^3\over 3}\right)+{15\over 4\alpha} \cr &\qquad+\ayspi{24}\left(1+{45\over 16\alpha}\right)+ {9\pi\over \alpha^2 y^6}e^{-2\alpha} \cr &\qquad\times\left[1+{23\over 4\alpha}-\ayspi6\left( 1+{35\over 16\alpha}\right)\right]\Biggr\}. \cr }\cr } $$ (2.47)

Величина \( E_{e+}+E_{e-} \) в (2.47) включает энергию покоя рождающихся пар и их кинетическую энергию без релятивистских поправок, а в \( P_{e+}+P_{e-} \) - учтены релятивистские поправки к давлению пар. В пределе очень малой плотности \( \lambda \ll 1 \), оставляя два члена разложения по \( \lambda \), из (2.46) получаются формулы, совпадающие с нерелятивистским пределом формул (2.38) при учете (2.42).

г) Нерелятивистский газ. В этом случае \( \alpha \sim \beta \gg 1 \) и вкладом позитронов можно пренебречь. Формулы (2.9) и (2.10) при этом сводятся к виду

$$ %\begin{displaymath} %\hbox{% %\begin{tabular}{l} %$\displaystyle{ \frac{\rho }{\mu _{Z}m_{u}}=\frac{\sqrt{2}}{\pi ^{2}}\left( \frac{m_{e}kT}{\hbar ^{2}}\right) ^{3/2}F_{1/2}(\beta -\alpha ) , }$ %$\displaystyle{ E_{e}=\frac{\sqrt{2}}{\pi ^{2}\rho }\left( \frac{m_{e}kT}{\hbar ^{2}}\right) ^{3/2}\left[ kTF_{3/2}(\beta -\alpha )+m_{e}c^{2}F_{1/2}(\beta -\alpha )\right] =\frac{m_{e}c^{2}}{\mu _{Z}m_{u}}+\frac{kT}{\mu _{Z}m_{u}}\frac{F_{3/2}(\beta -\alpha )}{F_{1/2}(\beta -\alpha )} , }$ %$\displaystyle{ P_{e}=\frac{2\sqrt{2}}{3\pi ^{2}}\left( \frac{m_{e}kT}{\hbar ^{2}}\right) ^{3/2}kTF_{3/2}(\beta -\alpha )=\frac{2}{3}\frac{\rho kT}{\mu _{Z}m_{u}}\frac{F_{3/2}(\beta -\alpha )}{F_{1/2}(\beta -\alpha )} , }$ %$\displaystyle{ S_{e}=\frac{\sqrt{2}}{\pi ^{2}}\frac{k}{\rho }\left( \frac{m_{e}kT}{\hbar ^{2}}\right) ^{3/2}\left[ \frac{5}{3}F_{3/2}(\beta -\alpha )-(\beta -\alpha )F_{1/2}(\beta -\alpha )\right] =\frac{k}{\mu _{Z}m_{u}}\left[ \frac{5}{3}\frac{F_{3/2}(\beta -\alpha )}{F_{1/2}(\beta -\alpha )}-(\beta -\alpha )\right] , }$ %\end{tabular}} %\end{displaymath} \eqalign{ &{\rho\over \muzmu}={\sqrt{2}\over \pi^2} \mkTh\Fba1, \cr &\eqalign{ E_{\mathrm{e}}&={\sqrt{2}\over \pi^2\rho} \mkTh\left[kT\Fba3+\mec{}2\Fba1\right] \cr &={\mec{}2\over \muzmu}+{kT\over \muzmu}{\Fba3\over \Fba1}, \cr }\cr &\eqalign{ P_{\mathrm{e}}&={2\sqrt{2}\over 3\pi^2} \mkTh kT\Fba3 \cr &={2\over 3}{\rho kT\over \muzmu}{\Fba3\over \Fba1}, \cr }\cr &\eqalign{ S_{\mathrm{e}}&={\sqrt{2}\over \pi^2}{k \over \rho} \mkTh\left[{5\over 3}\Fba3- (\beta-\alpha)\Fba1\right] \cr &={k\over \muzmu}\left[{5\over 3}{\Fba3\over \Fba1} -(\beta-\alpha)\right], \cr }\cr } $$ (2.48)

где \( F_{\nu }(\zeta ) \) - интегралы Ферми
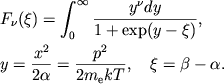$$ %\begin{displaymath} %F_{\nu }(\zeta )=\int ^{\infty }_{0}\frac{y^{\nu }dy}{1+exp(y-\zeta )} , \quad %y=\frac{x^{2}}{2\alpha }=\frac{p^{2}}{2m_{e}kT} , \quad %\zeta =\beta -\alpha . %\end{displaymath} \eqalign{ &F_\nu(\xi)=\intinf{y^\nu dy\over 1+\exp(y-\xi)}, \cr &y={x^2\over 2\alpha}={p^2\over 2m_{\mathrm{e}} kT},\quad \xi=\beta-\alpha. \cr } $$ (2.49)

В нерелятивистском пределе кинетическая энергия электронов отделяется от энергии покоя.

Если \( e^{-\beta +\alpha }\gg 1 \), то \( f_{e}\ll 1 \) и вырождение несущественно. В этом пределе получаем

$$ %\begin{displaymath} %\hbox{% %\begin{tabular}{l} %$\displaystyle{ F_{1/2}(\beta -\alpha )=e^{\beta -\alpha }\Gamma(3/2)[1-2^{-3/2}e^{\beta -\alpha }] , }$ %$\displaystyle{ F_{3/2}(\beta -\alpha )=e^{\beta -\alpha }\Gamma(5/2)[1-2^{-5/2}e^{\beta -\alpha }] . }$ %\end{tabular}} %\end{displaymath} \eqalign{ &\Fba1=e^{\beta-\alpha}\Gamma({3\over 2})[1-2^{-3/2}e^{\beta-\alpha}], \cr &\Fba3=e^{\beta-\alpha}\Gamma({5\over 2})[1-2^{-5/2}e^{\beta-\alpha}], \cr } $$ (2.50)

Первые члены в интегралах (2.50) приводят к термодинамическим функциям обычного газа (см. 1). С учетом поправок из первого соотношения (2.48) и (2.49) имеем

$$ \eqalign{ e^{\beta-\alpha}&={\rho\over \muzmu}\pi^{3/2}\sqrt{2}\left(\hbar^2\over m_{\mathrm{e}} kT\right)^{3/2} \cr &\qquad\times\left[1+{\rho\over \muzmu}{\pi^{3/2}\over 2}\left( \hbar^2\over m_{\mathrm{e}} kT\right)^{3/2}\right] \cr &=\sqrt{{2\over \pi}}{\alpha^{3/2}y^3\over 3}\left(1+\ayspi6\right)\,, \cr } $$

что приводит к термодинамическим функциям, следующим из (2.47), если в них пренебречь поправками на релятивизм ($\sim1/\alpha$) и рождение пар ( $\sim e^{-2\alpha }$). В пределе сильно вырожденного газа \( \beta -\alpha \gg 1 \) для вычисления интегралов Ферми (2.49) воспользуемся формулой (2.24). Оставляя два первых члена разложения, получаем
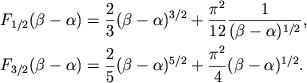$$ %\begin{displaymath} %\hbox{% %\begin{tabular}{l} %$\displaystyle{ F_{1/2}(\beta -\alpha )=\frac{2}{3}(\beta -\alpha )^{3/2}+\frac{\pi ^{2}}{12}\frac{1}{(\beta -\alpha )^{1/2}} , }$ %$\displaystyle{ F_{3/2}(\beta -\alpha )=\frac{2}{5}(\beta -\alpha )^{5/2}+\frac{\pi ^{2}}{4}(\beta -\alpha )^{1/2} . }$ %\end{tabular}} %\end{displaymath} \eqalign{ &\Fba1={2\over 3}(\beta-\alpha)^{3/2}+{\pi^2\over 12} {1\over (\beta-\alpha)^{1/2}}, \cr &\Fba3={2\over 5}(\beta-\alpha)^{5/2}+{\pi^2\over 4} (\beta-\alpha)^{1/2}. \cr } $$ (2.51)

Определяя из первого соотношения (2.48)

$$ %\begin{displaymath} %\beta -\alpha =\frac{1}{2}\left( \frac{3\pi ^{2}\rho }{\mu _{Z}m_{u}}\right) ^{2/3}\frac{\hbar ^{2}}{m_{e}kT}\left[ 1-\frac{\pi ^{2}}{3}\left( \frac{\mu _{Z}m_{u}}{3\pi ^{2}\rho }\right) ^{4/3}\left( \frac{m_{e}kT}{\hbar ^{2}}\right) ^{2}\right] =\frac{\alpha y^{2}}{2}\left( 1-\frac{\pi ^{2}}{3\alpha ^{2}y^{4}}\right) , %\end{displaymath} \eqalign{ \beta-\alpha&={1\over 2}\left(3\pi^2\rho\over \muzmu\right)^{2/3} {\hbar^2\over m_{\mathrm{e}} kT} \cr &\qquad\times\left[1-{\pi^2\over 3} \left(\muzmu \over 3\pi^2\rho\right)^{4/3} \left(m_{\mathrm{e}} kT\over \hbar^2\right)^2\right] \cr &={\alpha y^2\over 2}\left(1-{\pi^2\over 3\alpha^2 y^4}\right), \cr } $$ (2.52)

получаем термодинамические функции, следующие из (2.32), если пренебречь в них релятивистскими поправками ( $\sim1/\alpha^{2}$). Из (2.48) следует, что адиабата нерелятивистского электронного газа имеет вид \( T\rho ^{-2/3}=const \), \( P\rho ^{-5/3}=const \) вне зависимости от степени вырождения. При этом \( E_{t,\mbox{кин}}=\frac{3}{2}P_{e} \), где \( E_{t,\mbox{кин}}=E_{e}-\frac{m_{e}c^{2}}{\mu _{Z}m_{u}} \). Та же связь \( \rho \), \( T \) и \( P \) вдоль адиабаты имеет место для любого одноатомного идеального нерелятивистского газа с постоянными \( \mu \) и \( \mu _{Z} \).

д) Ультрарелятивистский газ. Когда кинетическая энергия электронов много больше их энергии покоя, величиной \( \alpha \) в интегралах (2.10) можно пренебречь, что, с учетом определения (2.49) позволит записать их в виде


$$ %\begin{displaymath} %I_{n\pm }=F_{2}(\pm \beta ) , \quad I_{P\pm }=I_{E\pm }=F_{3}(\pm \beta ) %\end{displaymath} \Ipm{n}=F_2(\pm\beta).\quad \Ipm{P}=\Ipm{E}=F_3(\pm\beta). $$ (2.53)

В ультрарелятивистском равновесном газе всегда имеет место \( \beta \geq 0 \) и вырождение не может быть малым ввиду интенсивного рождения пар.

Интегралы Ферми целого индекса обладают свойствами, позволяющими выразить термодинамические функции ультрарелятивистского газа в виде полиномов по \( T \) и \( \beta \) [166]. Из (2.49) легко показать, что4


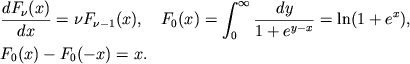$$ %\begin{displaymath} %\hbox{% %\begin{tabular}{ll} %$\displaystyle{ \frac{dF_{\nu }(x)}{dx}=\nu F_{\nu -1}(x) , }$ \qquad & %$\displaystyle{ F_{0}(x)=\int ^{\infty }_{0}\frac{dy}{1+e^{y-x}}=\ln (1+e^{x}) }$ %$\displaystyle{ F_{0}(x)-F_{0}(-x)=x . }$ %\end{tabular}} %\end{displaymath} \eqalign{ &{dF_\nu(x)\over dx}=\nu F_{\nu -1}(x),\quad F_0(x)=\intinf{dy\over 1+e^{y-x}}=\ln(1+e^x), \cr &F_0(x)-F_0(-x)=x. \cr } $$ (2.54)

Интегрируя последовательно первое соотношение (2.54), получаем
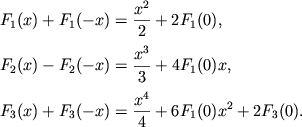$$ %\begin{displaymath} %\hbox{% %\begin{tabular}{l} %$\displaystyle{ F_{1}(x)+F_{1}(-x)=\frac{x^{2}}{2}+2F_{1}(0) , \quad F_{2}(x)+F_{2}(-x)=\frac{x^{3}}{3}+4F_{1}(0)x , }$ %$\displaystyle{ F_{3}(x)+F_{3}(-x)=\frac{x^{4}}{4}+6F_{1}(0)x^{2}+2F_{3}(0) . }$ %\end{tabular}} %\end{displaymath} \eqalign{ &F_1(x)+F_1(-x)={x^2\over 2}+2F_1(0), \cr \noalign{\smallskip} &F_2(x)-F_2(-x)={x^3\over 3}+4F_1(0)x, \cr \noalign{\smallskip} &F_3(x)+F_3(-x)={x^4\over 4}+6F_1(0)x^2+2F_3(0). \cr } $$ (2.55)

Интегралы \( F_{\nu }(0) \) приведены в (2.36), откуда имеем

\begin{displaymath} F_{1}(0)=\pi ^{2}/12 ; \quad F_{2}(0)=\frac{3}{2}\zeta (3)=1.803 ; \quad F_{3}(0)=7\pi ^{4}/120 . \end{displaymath}

В итоге получаем значения термодинамических функций для \( e^{-}e^{+} \)- пар в виде
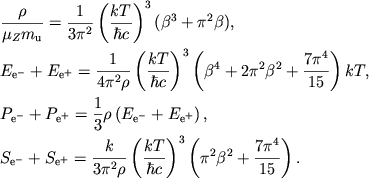$$ \eqalign{ &{\rho\over \muzmu}={1\over 3\pi^2}\left(kT\over \hbar c\right)^3 (\beta^3+\pi^2\beta), \cr &\summp{E}={1\over 4\pi^2 \rho}\left(kT\over \hbar c\right)^3 \left(\beta^4+2\pi^2\beta^2+{7\pi^4\over 15}\right)kT, \cr &\summp{P}={1\over 3}\rho\left(E_{\mathrm{e^-}}+E_{\mathrm{e^+}}\right), \cr &\summp{S}={k\over 3\pi^2 \rho}\left(kT\over \hbar c\right)^3 \left(\pi^2\beta^2+{7\pi^4\over 15}\right). \cr } $$ (2.56)

В пределе сильного вырождения \( \beta \gg (1,\alpha ) \) вклад позитронов пренебрежимо мал, и из первого соотношения (2.56) и (2.29) имеем

$$ %\begin{displaymath} %\beta =\left( \frac{3\pi ^{2}\rho }{\mu _{Z}m_{u}}\right) ^{1/3}\frac{\hbar c}{kT}\left[ 1-\frac{\pi ^{2}}{3}\left( \frac{\mu _{Z}m_{u}}{3\pi ^{2}\rho }\right) ^{2/3}\left( \frac{kT}{\hbar c}\right) ^{2}\right] =\alpha y\left( 1-\frac{\pi ^{2}}{3\alpha ^{2}y^{2}}\right) . %\end{displaymath} \eqalign{ \beta&=\left(3\pi^2\rho\over \muzmu\right)^{1/3}{\hbar c\over kT} \left[1-{\pi^2\over 3}\left(\muzmu\over 3\pi^2\rho\right)^{2/3} \left(kT\over \hbar c\right)^2\right] \cr &=\alpha y\left(1-\piay{}232{}2\right). \cr } $$

Это приводит к термодинамическим функциям (2.33) без членов \(\sim y^{-2} \), задающих отклонения от ультрарелятивизма. В ультрарелятивистском газе малой плотности при \( \beta \rightarrow 0 \) имеем

$$ %\begin{displaymath} %\beta =\frac{3\rho }{\mu _{Z}m_{u}}\left( \frac{\hbar c}{kT}\right) ^{3}\left[ 1-\frac{1}{\pi ^{6}}\left( \frac{3\pi ^{2}\rho }{\mu _{Z}m_{u}}\right) ^{2}\left( \frac{\hbar c}{kT}\right) ^{6}\right] =\frac{y^{3}\alpha ^{3}}{\pi ^{2}}\left( 1-\frac{y^{6}\alpha ^{6}}{\pi ^{6}}\right) , %\end{displaymath} \eqalign{ \beta&={3\rho\over \muzmu}\left({\hbar c\over kT}\right)^3 \left[1-{1\over \pi^6}\left(3\pi^2\rho\over \muzmu\right)^2 \left(\hbar c\over kT \right)^6\right] \cr &={\ya3\over \pi^2}\left(1-{\ya6\over \pi^6}\right) \cr } $$

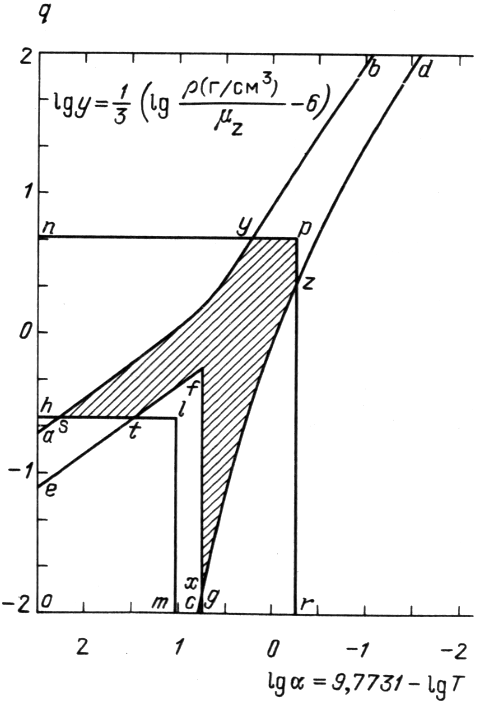что приводит к термодинамическим функциям, следующим из (2.41) без учета отклонений от ультрарелятивизма \(\sim \alpha ^{-2} \). Из (2.56) следует, что вдоль адиабаты ультрарелятивистского газа выполняются соотношения \( T\rho ^{-1/3}=const \) , \( P\rho ^{-4/3}=const \). Из полученных выше явных выражений тер модинамических функций в зависимости от \( \rho \) и \( T \) легко, с помощью (1.11)-(1.17), найти явные выражения для адиабатических показателей и теплоемкостей во всех предельных случаях. Области применимости асимптотических формул с точностью $\sim$1% изображены на рис. 2. Некоторые асимптотические формулы с большим числом членов разложения даны в работе [166], рассчитанные по ним таблицы и интерполяционные коэффициенты приведены в [167], см. также [67a].

Рис. 2. Области применимости приближенных асимптотических формул на плоскости $\lg y = -\frac{1}{3} (\lg (\rho/\mu_Z) - 6,0116)$, $\lg a = 9,7731 - \lg T$:
A) левее линии ayb применимо приближение вырожденного газа с поправками (2.30),
B) правее линии czd - приближение малой плотности (2.38),
C) внутри области oefg - приближение почти невырожденного почти нерелятивистского газа (2.46),
D) ohlm - область применимости приближения нерелятивистского газа (2.48),
Е) правее и выше ломаной npr применимо приближение ультрарелятивистского газа (2.56).
В следующих областях применимы различные приближения: 1) nqby - приближения А и Е,
2) правее ломаной rzd - приближения В и Е,
3) cxg - приближения В и С,
4) oetlm - приближения С и D,
5) ahs - приближения А и D.
Заштрихована область, где необходим численный расчет интегралов, входящих в термодинамические функции, например, методом Гаусса


Таблица 4. Корни и коэффициенты для вычисления интегралов (2.57) методом Гаусса при \( n=5 \), при \( p=0,1,2,3,4 \) (см., например [29])
Корни $x_{i}$ и коэффициенты \( A_{i} \) \( p=0 \) \( p=1 \) \( p=2 \) \( p=3 \) \( p=4 \)
\( x_{1} \) 0.26356 0.61703 1.0311 1.4906 1.9859
\( x_{2} \) 1.4134 2.1130 2.8372 3.5813 4.3417
\( x_{3} \) 3.5964 4.6108 5.6203 6.6270 7.6320
\( x_{4} \) 7.0858 8.3991 9.6829 10.944 12.188
\( x_{5} \) 12.641 14.260 15.828 17.357 18.852
\( A_{1} \) 0.52176 0.34801 0.52092 1.2510 4.1856
\( A_{2} \) 0.39867 0.50228 1.0667 3.2386 12.877
\( A_{3} \) 0.075942 0.14092 0.38355 1.3902 6.3260
\( A_{4} \) 3.6118(-3) 8.7199(-3) 0.028564 0.11904 0.60475
\( A_{5} \) 2.3370 (-5) 6.8973 (-5) 2.6271 (-4) 1.2328(-3) 6.8976 (-3)

е) Анализ общего случая. При отсутствии малых параметров для расчета термодинамических функций нужно вычислять интегралы (2.10) численно. Весьма эффективным является метод, аналогичный методу Гаусса [137], и использованный для этих целей в работе [46]. Подынтегральные выражения в (2.10) представляются в виде \( f(x)x^{p}e^{-x} \), где функция \( f(x) \) ограничена на любом конечном интервале и хорошо аппроксимируется каким-нибудь полиномом степени \( \leq 2n-1 \) на интервале \( (0,N) \) при достаточно большом \( N \). Вычисления проводятся по следующей квадратурной формуле:

$$ %\begin{displaymath} %\int ^{\infty }_{0}f(x)x^{p}e^{-x}dx = \sum _{i=1}A_{i}f(x_{i}) , %\end{displaymath} \intinf f(x)x^p e^{-x}dx=\sum_{i=1}^n A_i f(x_i), $$ (2.57)

где \( x_{i} \) - корни полинома Лагерра \( L^{(p)}_{n} \), а коэффициенты \( A_{i} \) определяются системой линейных уравнений

\begin{displaymath} \sum ^{n}_{i=1}A_{i}x^{k}_{i}=(k+\rho)!\,, \quad k=0,1,\ldots,n-1\,. \end{displaymath}

Формула (2.57) является точной, если \( f(x) \) - полином степени \( \leq 2n-1 \). Это следует из условия ортогональности полиномов Лагерра \( L^{(p)}_{n} \) на промежутке \( (0,\infty ) \) с весом \( x^{p}e^{-x} \). Значение \( p=2 \) можно использовать при вычислении \( I_{n} \) и \( p=3 \) для \( I_{E} \) и \( I_{p} \) из (2.10). Значения \( x_{i} \) и \( A_{i} \) для пятиточечной схемы (и = 5) приведены в таблице 4 [29] для \( p=0,1,2,3,4 \).

Выражения для адиабатического показателя \( \gamma _{1} \) и теплоемкостей в общем случае при постоянном ядерном составе получены в [46]

$$ %\begin{displaymath} %\hbox{% %\begin{tabular}{l} %$\displaystyle{ \gamma _{1}=\left( k+\frac{N^{2}}{M}\right) \left[ 1+\frac{(\mu _{N}/\mu _{Z})\pi ^{4}}{45(I_{n-}-I_{n+})}+\frac{(\mu _{N}/\mu _{Z})(I_{p-}+I_{p+})}{3(I_{n-}-I_{n+})}\right] ^{-1} , }$ %$\displaystyle{ C_{\nu }=\frac{k}{\mu _{N}m_{u}}M , \quad C_{p}=\frac{k}{\mu _{N}m_{u}}\left( M+\frac{N^{2}}{k}\right) , }$ %\end{tabular}} %\end{displaymath} \eqalign{ & \eqalign{ \gamma_1 &=\left(\kappa+{N^2\over M}\right)\times \cr &\times \left[1+ {(\mu_N/\mu_Z)\pi^4\over 45(I_{n-}-I_{n+})} \,+{(\mu_N/\mu_Z)(I_{P-}-I_{P+})\over 3(I_{n-}-I_{n+})} \right]^{-1}, \cr} \cr & C_v={k\over \mu_N m_{\mathrm{u}}}M, \quad C_p={k\over \mu_N m_{\mathrm{u}}}\left(M+{N^2\over \kappa}\right), \cr} $$ (2.58)

где
$$ %\begin{displaymath} %\hbox{% %\begin{tabular}{l} %$\displaystyle{ M=\frac{3}{2}+\frac{\mu _{N}/\mu _{Z}}{I_{n-}-I_{n+}}\left\{ \frac{4\pi ^{4}}{15}+\sum _{+,-}(3I_{E\pm }+I_{P\pm }+\alpha ^{2}I_{5\pm }+\alpha ^{2}I_{6\pm })- \right. }$ %$\displaystyle{ \left. \qquad\qquad -\frac{\left[ 3\left( I_{n-}-I_{n+}\right) +\alpha ^{2}\left( I_{4-}-I_{4+}\right) \right] ^{2}}{\sum _{+,-}\left( I_{5\pm }+I_{6\pm }\right) }\right\} , }$ %$\displaystyle{ N=1+\frac{\mu _{N}/\mu _{Z}}{3(I_{n-}-I_{n+})}\left\{ \frac{4\pi ^{4}}{15}+\sum _{+,-}(3I_{E\pm }+I_{P\pm })- \right. }$ %$\displaystyle{ \qquad\qquad \left. -\frac{3(I_{n-}-I_{n+})\left[ 3\left( I_{n-}-I_{n+}\right) +\alpha ^{2}\left( I_{4-}-I_{4+}\right) \right] }{\sum _{+,-}\left( I_{5\pm }+I_{6\pm }\right) }\right\} , }$ %$\displaystyle{ k=1+\frac{\mu _{N}}{\mu _{Z}}\frac{I_{n-}-I_{n+}}{\sum _{+,-}(I_{5\pm }+I_{6\pm })} , }$ %$\displaystyle{ I_{4\pm }=\int ^{\infty }_{0}\frac{dx}{1+\exp \left( \sqrt{x^{2}+\alpha ^{2}}\pm \beta \right) } , }$ %$\displaystyle{ I_{5\pm }=\int ^{\infty }_{0}\frac{\sqrt{x^{2}+\alpha ^{2}}dx}{1+\exp \left( \sqrt{x^{2}+\alpha ^{2}}\pm \beta \right) } , }$ %$\displaystyle{ I_{6\pm }=\int ^{\infty }_{0}\frac{x^{2}dx}{\sqrt{x^{2}+\alpha ^{2}}\left[ 1+\exp \left( \sqrt{x^{2}+\alpha ^{2}}\pm \beta \right) \right] } . }$ %\end{tabular}} %\end{displaymath} \eqalign{ &\eqalign{ M&={3\over 2}+{\mu_N/\mu_Z\over \sumI{n}}\Biggl\{{4\pi^4\over 15} +\sum_{+,-}\left(3I_{E\pm}+I_{P\pm}+\alpha^2I_{5\pm} +\alpha^2 I_{6\pm}\right) \cr &\qquad-{\left[3(\sumI{n})+\alpha^2(\sumI4)\right]^2\over \sum_{+,-} (I_{5\pm}+I_{6\pm})}\Biggr\}, \cr }\cr &\eqalign{ N&=1+{\mu_N/\mu_Z\over 3\left(\sumI{n}\right)}\Biggl\{{4\pi^4\over 15}+ \sum_{+,-}\left(3I_{E\pm}+I_{P\pm}\right) \cr &\qquad-{3\left(\sumI{n}\right)\left[3\left(\sumI{n}\right)+ \alpha^2\left(\sumI4\right)\right]\over \sum_{+,-} (I_{5\pm}+I_{6\pm})}\Biggr\}, \cr }\cr &\kappa=1+{\mu_N\over \mu_Z}{\sumI{n}\over \sum_{+,-} (I_{5\pm}+I_{6\pm})}, \cr &\Ipm4=\intinf{dx\over 1+\exp\left(\sqrt{x^2+\alpha^2}\pm\beta\right)}, \cr &\Ipm5=\intinf{\sqrt{x^2+\alpha^2}dx\over 1+\exp\left(\sqrt{x^2+\alpha^2}\pm\beta\right)}, \cr &\Ipm6=\intinf{x^2 dx\over \sqrt{x^2+\alpha^2} \left[1+\exp\left(\sqrt{x^2+\alpha^2}\pm\beta\right)\right]}. \cr } $$ (2.59)

Безразмерный химический потенциал \( \beta \) вдоль изэнтропы удовлетворяет уравнению

$$ T{d\beta\over dT}={M\over N}{\sumI{n}\over \sum_{+,-}(I_{5\pm}+I_{6\pm})}- {3(\sumI{n})+\alpha^2(\sumI{4})\over \sum_{+,-}(I_{5\pm}+I_{6\pm})}. $$ (2.60)

Зависимости \( \gamma _{1}(T) \), \( C_{\nu }(T) \), \( C_{p}/C_{\nu }(T) \) для чистого железа (\( A=56 \), \( \mu _{N}/\mu _{Z}=Z=26 \)), построенные по формулам (2.58)-(2.60) в [46], приведены на рис. 3-5.

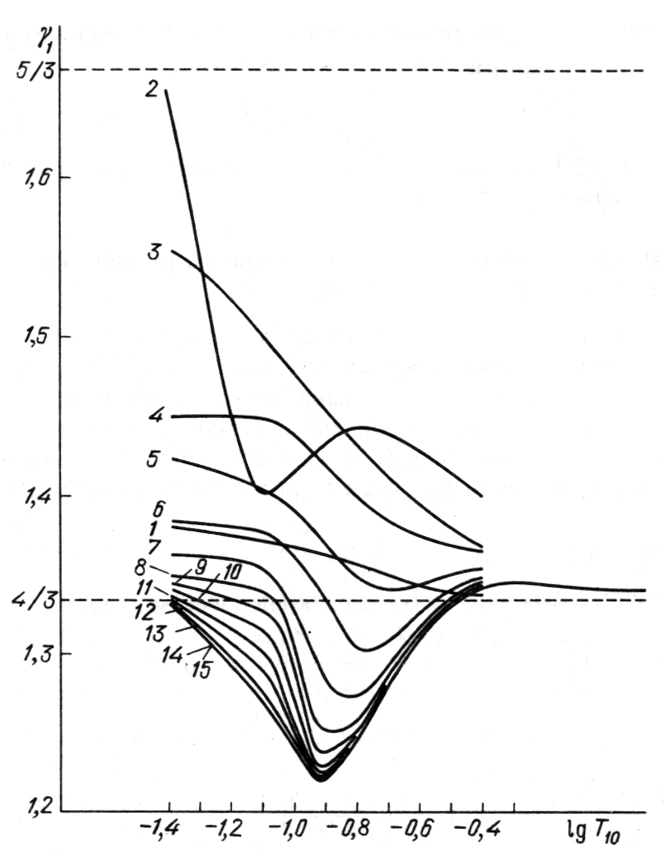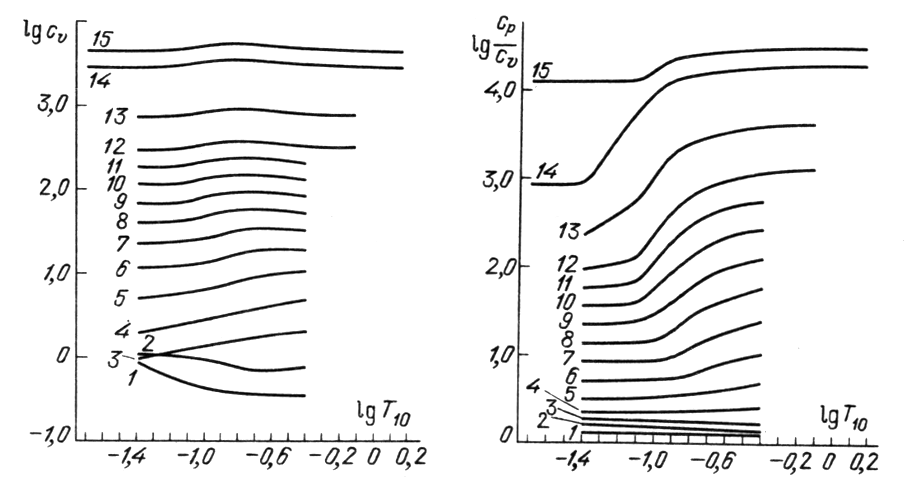Рис. 3. Зависимость показателя адиабаты $\gamma_1$ от температуры $Т$ для чистого железа вдоль изэнтроп, построенных на рис. 6

Рис. 4. Зависимость теплоемкости при постоянном объеме $c_v$ от температуры $Т$ для чистого железа вдоль изэнтроп, построенных на рис. 6
Рис. 5. Зависимость теплоемкости при постоянном объеме $c_v$ от температуры $Т$ для чистого железа вдоль изэнтроп, построенных на рис. 6

Задача. Найти релятивистские поправки к адиабатическому показателю \( \gamma _{1} \) в идеальном газе.

Ответ. \( \gamma _{1}=\frac{5}{3}\left( 1-\frac{\mu }{\mu _{Z}}\frac{kT}{m_{e}c^{2}}\right) \). При этом использованы формулы (1.11), (2.13), (2.15), (2.18) и (2.47), где опущены поправки на вырождение и рождение пар \( \sim \alpha ^{3/2}y^{3} \) и \( e^{-2\alpha } \).


<< 1. Идеальный газ с | Оглавление | 3. Уравнение состояния при ... >>

Публикации с ключевыми словами: Эволюция звезд - физические процессы
Публикации со словами: Эволюция звезд - физические процессы
См. также:
Все публикации на ту же тему >>

Обсудить эту публикацию
Оценка: 2.6 [голосов: 87]
 
О рейтинге
Версия для печати Распечатать

Астрометрия - Астрономические инструменты - Астрономическое образование - Астрофизика - История астрономии - Космонавтика, исследование космоса - Любительская астрономия - Планеты и Солнечная система - Солнце

Астронет | Научная сеть | ГАИШ МГУ | Поиск по МГУ | О проекте | Авторам

Комментарии, вопросы? Пишите: info@astronet.ru или сюда

Rambler's Top100 Яндекс цитирования