Астронет > Физические вопросы теории звездной эволюции

по текстам по ключевым словам в глоссарии по сайтам перевод по каталогу

<< Предисловие | Оглавление | 2. Релятивистский газ с вырождением >>

Часть I. ФИЗИКА ЗВЕЗДНОЙ МАТЕРИИ

Глава 1. Термодинамические свойства вещества

Разделы

Вещество большинства звезд имеет высокую температуру и сравнительно умеренную плотность. В этих условиях кинетическая энергия частиц много больше энергии взаимодействия между ними и модель нерелятивистского, невырожденного идеального газа оказывается хорошим приближением к реальности. Термодинамические свойства вещества планет, например. Земли, изучены гораздо хуже. Температура их при той же плотности значительно ниже и вещество находится в жидкой и твердой фазах, исследование которых сопряжено с существенными трудностями.

В недрах звезд вещество и излучение находятся в термодинамическом равновесии, которое устанавливается быстрыми процессами столкновений частиц, поглощением и испусканием фотонов. Излучение, наряду с газом, создает давление, противодействующее силе тяжести.

Вещество звезд состоит из различных химических элементов, основными из которых являются водород и гелий. На Солнце, например, они составляют в сумме более 98,5% плотности вещества. Остальная часть массы Солнца состоит из смеси практически всех стабильных изотопов таблицы Менделеева. В табл. 1 указано содержание наиболее обильных элементов, наблюдаемых на Солнце [5]. При изменении от центра до поверхности звезды температуры на три-четыре порядка и плотности на ~ 10 порядков изменяется состояние ионизации вещества.

В центральных областях звезд с $\emph{М} \geq \emph{М}_{\odot }$ все атомы практически полностью ионизованы.

Пусть $i$ - номер химического элемента, который может находиться в различных состояниях ионизации от нейтрального ( $j=0$ ) до полностью ионизованного ( $j=i$ ). Обозначим через $\epsilon_{\textrm{ij}}$ энергию связи $j$ -кратно ионизованного иона элемента $i$ , определяемую так, что для полностью ионизованного иона $\epsilon_{\textrm{ij}}$ = 0. Удельная энергия Е (эрг г^-1), давление Р (дин см^-2) и удельная энтропия S (эрг г^-1 К^-1) данной смеси атомов, ионов и электронов с излучением имеют вид [145] .

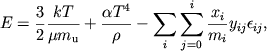
$%\begin{displaymath} %E=\frac{3}{2}\frac{kT}{\mu m_{u}}+\frac{aT^{4}}{\rho }-\Sigma _{i}\Sigma ^{i}_{j=0}\frac{x_{i}}{m_{i}}y_{ij}\epsilon _{ij} \end{displaymath} E={3\over2}{kT\over\mu m_{\rm u}}+ {\alpha T^4\over\rho}- \sum_i \sum_{j=0}^i {x_i\over m_i} y_{ij} \epsilon_{ij},$

(1.1)

$%\begin{displaymath}P=\frac{\rho kT}{\mu m_{u}}+\frac{1}{3}aT^{4} \end{displaymath} P = {\rho k T\over\mu m_{\rm u}}+{1\over 3}\alpha T^4,$

(1.2)

$%\begin{displaymath}S=\frac{k}{\rho }\Sigma _{i}\Sigma _{j=0}^{i}n_{ij}\left\{ \frac{5}{2}+\ln\left[ \left( \frac{m_{i}kT}{2\pi \hbar ^{2}}\right) ^{3/2}\frac{g_{ij}}{n_{ij}}\right] \right\} +\frac{k}{\rho }n_{e}\left\{ \frac{5}{2}+\ln\left[ \left( \frac{m_{e}kT}{2\pi \hbar }\right) ^{3/2}\frac{2}{n_{e}}\right] \right\} +\frac{4}{3}\frac{aT^{3}}{\rho } \end{displaymath} \eqalign{ S&={k\over\rho}\sum_i \sum_{j=0}^i n_{ij}\left\{ {5\over 2} \ln\left[ \left(m_i k T\over 2\pi \hbar^2\right)^{3/2} {g_{ij}\over n_{ij}}\right]\right\}\cr &\qquad+{k\over \rho} n_{\rm e} \left\{ {5\over 2}+\ln\left[ \left(m_{\rm e} k T\over 2\pi \hbar^2\right)^{3/2} {2\over n_{\rm e}} \right]\right\} +{4\over 3} {a T^3\over \rho},\cr }$

(1.3)

Здесь использованы обозначения:

$\rho$ - плотность,

$T$ - температура,

$k=1.38067\cdot 10^{-16}\mbox{~эрг}\cdot \mbox{K}^{-1}$ - постоянная Больцмана,

$\hbar =1.0546\cdot 10^{-27}\mbox{~эрг}\cdot \mbox{с}$ - постоянная Планка,

$a=\pi ^{2}k^{4}/15\hbar ^{3}c^{3}=7.565\cdot 10^{-15}\mbox{~эрг}\cdot \mbox{см}^{-3}\cdot \mbox{K}^{-4}$ - постоянная плотности излучения,

$c=2.9979\cdot 10^{10}\mbox{~см}\cdot \mbox{с}^{-1}$ - скорость света в вакууме,

$x_{ij}$ - массовая доля элемента с атомным номером i,

Таблица 1. Распространенность наиболее обильных химических элементов (Солнце, [5])

Элемент	Символ	Атомный номер	Атомная масса	Десятичный логарифм распространенности
Элемент	Символ	Атомный номер	Атомная масса	по числу атомов	по массе
Водород	H	1	1.0080	12.00	12.00
Гелий	He	2	4.0026	10.93	11.53
Углерод	C	6	12.0111	8.52	9.60
Азот	N	7	14.0067	7.96	9.11
Кислород	О	8	15.9994	8.82	10.02
Неон	Ne	10	20.179	7.92	9.22
Натрий	Na	11	22.9898	6.25	7.61
Магний	Mg	12	24.305	7.42	8.81
Алюминий	Al	13	26.9815	6.39	7.78
Кремний	Si	14	28.086	7.52	8.97
Фосфор	P	15	30.9738	5.52	7.01
Сера	S	16	32.06	7.20	8.71
Хлор	Cl	17	35.453	5.6	7.2
Аргон	Аг	18	39.948	6.8	8.4
Кальций	Са	20	40.08	6.30	7.90
Хром	Сг	24	51.996	5.85	7.57
Марганец	Mn	25	54.9380	5.40	7.14
Железо	Fe	26	55.847	7.60	9.35
Никель	Ni	28	58.71	6.30	8.07
Относительное содержание по массе:			Число нуклонов на ядро,
Водород		X $_{\textrm{H}}$ =0.73	$\mu$ $_{\textrm{n}}$ =1.26
Гелий		X $_{\textrm{He}}$ =0.25	Средняя атомная масса при полной ионизации
Прочие элементы		$\Sigma$ x $_{\textrm{i}}$ =0.017	$\mu$ =0.60

$y_{ij}$ - степень $j$ -кратной ионизации $j$ -го элемента, так что $\sum _{j=0}^{i}y_{ij}=1$ ,

$m_{i}\approx A_{i}m_{u}$ - масса ядра атома с номером $i$ и атомной массой $A_{i}\geq 4$

$m_{u}=1.66057\cdot 10^{-24}$ г - атомная единица массы, равная 1/12 массы изотопа $^{12}C$ ,

$m_{e}=9.10953\cdot 10^{-28}$ г - масса электрона¹,

$%\begin{displaymath}n_{ij}=x_{i}\rho y_{ij}/m_{i} \mbox{~см}^{-3} \end{displaymath} n_{ij}=x_i \rho y_{ij}/m_i \mbox{\rm~cm}^{-3}$

(1.4)

- концентрация ионов элемента $i$ в $j$ -м состоянии ионизации,

$g_{ij}$ - статистический вес иона $i$ -го элемента в $j$ -м состоянии ионизации,

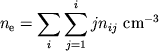$%\begin{displaymath}n_{e}=\Sigma _{i}\Sigma _{j=1}^{i}jn_{ij} \mbox{~см}^{-3} \end{displaymath} n_{\rm e}=\sum_i \sum_{j=1}^i jn_{ij} \mbox{\rm~cm}^{-3}$

(1.5)

- концентрация электронов в условиях электронейтральности,

$%\begin{displaymath}\mu =\left[ \Sigma _{i}\frac{m_{u}}{m_{i}}x_{i}\Sigma ^{i}_{j=0}(1+j)y_{ij}\right] ^{-1} \end{displaymath} \mu=\left[\sum_i {m_{\rm u}\over m_i} x_i \sum_{j=0}^i(1+j) y_{ij} \right]^{-1}$

(1.6)

- количество нуклонов на одну частицу газа (средняя атомная масса).

В полностью ионизованном газе, состоящем из водорода, гелия и других элементов с $A_{i}\approx 2i\gg 1$ , имеем

$%\begin{displaymath} %\mu =\left[ 2x_{H}+\frac{3}{4}x_{He}+\frac{1}{2}x_{A}\right] ^{-1},~ %x_{A}=\Sigma _{i\geq 6}x_{i} ,~ %m_{He}\approx 4m_{u} ,~ %m_{H}\approx m_{u} \end{displaymath} \eqalign{ &\mu\simeq\left[2x_{\rm H}+{3\over 4}x_{\rm He}+{1\over 2} x_A\right]^{-1}, \qquad x_A=\sum\limits_{i\ge 6}x_i, \cr &m_{\rm He}\approx 4 m_{\rm u}, \quad m_{\rm H}\approx m_{\rm u}. \cr}$

(1.7)

Энергия в (1.1) отсчитывается от энергии покоя полностью ионизованных ионов и электронов. Степени ионизации элементов в термодинамическом равновесии определяются формулой Саха [145]

$%\begin{displaymath}\frac{y_{i,j-1}}{y_{i,j}}=n_{e}\frac{g_{i,j-1}}{2g_{ij}}\left( \frac{2\pi \hbar ^{2}}{m_{e}kT}\right) ^{3/2}e^{^{I_{ij}/kT}}=n_{e}K(T) . \end{displaymath} {y_{i,j-1}\over y_{ij}}=n_{\rm e}{g_{i,j-1}\over 2g_{ij}}\left( 2 \pi \hbar^2\over m_{\rm e}kT \right)^{3/2} e^{I_{ij}/kT}=n_{\rm e} K(T)$

(1.8)

Здесь $I_{ij}=\epsilon _{i,j-1}-\epsilon _{ij}$ - энергия (потенциал) ионизации $i$ -го электрона, $I_{i0}=0$ . Энергии ионизации наиболее обильных элементов приведены в табл. 2. Для нахождения степени ионизации элементов в смеси необходимо решить систему уравнений (1.8) с учетом (1.4), (1.5). Аналитическое ре шение получается в случае однократной ионизации одного ( $i$ -го) сорта атомов

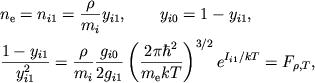
$\eqalign{ &n_{\rm e}=n_{i1}={\rho\over m_i} y_{i1}, \qquad y_{i0}=1-y_{i1}, \cr &{1-y_{i1}\over y_{i1}^2}={\rho\over m_i}{g_{i0}\over 2g_{i1}} \left( 2 \pi \hbar^2\over m_{\rm e}kT \right)^{3/2} e^{I_{i1}/kT}= F_{\rho,T}, \cr}$

откуда

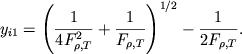$%\begin{displaymath}y_{i1}=\left( \frac{1}{4F_{\rho ,T}^{2}}+\frac{1}{F_{\rho ,T}}\right) ^{1/2}-\frac{1}{2F_{\rho ,T}}.\end{displaymath} y_{i1}=\left({1\over 4F_{\rho,T}^2}+{1\over F_{\rho,T}}\right)^{1/2} -{1\over 2F_{\rho,T}}.$

(1.9)

Таблица 2. Потенциалы ионизации и полные моменты внешних электронных оболочек наиболее обильных элементов [180].

Атомный номер	Элемент	Потенциалы ионизации, эВ	Полные моменты
1	H $^{-}$ ,H	0.747; 13.5985	0; 1/2
2	He	24.5876; 54.418	0; 1/2; 0
6	C	11.260; 24.284; 47.89; 64.49	0; 1/2; 0; 1/2
7	N	14.534; 29.602; 47.45; 77.47	3/2; 0; 1/2; 0
8	O	13.618; 35.118; 54.94; 77.41	2; 3/2; 0; 1/2
10	Ne	21.565; 40.964; 63.46; 97.12	0; 3/2; 2; 3/2
11	Na	5.1391; 47.287; 71.64; 98.92	1/2; 0; 3/2; 2
12	Mg	7.646; 15.035; 80.15; 109.2	0; 1/2; 0; 3/2
13	Al	5.9858; 18.828; 28.448; 120	1/2; 0; 1/2; 0
14	Si	8.152; 16.346; 33.493; 45.14	0; 1/2; 0; 1/2
15	P	10.49; 19.73; 30.18; 51.47	3/2; 0; 1/2; 0
16	S	10.36; 23.33; 34.83; 47.31	2; 3/2; 0; 1/2
17	Cl	12.968; 23.81; 39.61; 53.47	3/2; 2; 3/2; 0
18	Ar	15.760; 27.63; 40.74; 59.81	0; 3/2; 2; 3/2
20	Ca	6.113; 11.872; 50.91; 67.10	0; 1/2; 0; 3/2
24	Cr	6.766; 16.50; 30.96; 49	3; 5/2; 0; 3/2
25	Mn	7.4368; 15.640; 33.67; 51.2	5/2; 2; 5/2; 0
26	Fe	7.87; 16.18; 30.65; 54.8	4; 9/2 4; 5/2
28	Ni	7.63; 18.17; 35.2; 54.9	4; 5/2; 4; 9/2
1 эВ = 11.604 К		X $_{0}$ ; X $_{+}$ ; X $_{++}$ ; X $_{+++}$	X $_{0}$ ; X $_{+}$ ; X $_{++}$ ; X $_{+++}$

При исследовании звездной эволюции часто необходимо знать значения адиабатических показателей

$\gamma_1=\left(\partial\ln P\over \partial\ln\rho\right)_S, \quad \gamma_2=\left(\partial\ln T\over \partial\ln P\right)_S, \quad \gamma_3=\left(\partial\ln T\over \partial\ln\rho\right)_S,$

и теплоемкостей

$%\begin{displaymath} %c_{\upsilon }=T\left( \frac{\partial S}{\partial T}\right) _{\rho } , \quad %c_{p}=\left( \frac{\partial S}{\partial T}\right) _{P}. %\end{displaymath} c_v=T\left(\partial S\over \partial T\right)_\rho,\quad c_p=T\left(\partial S\over \partial T\right)_P.$

В условиях неполной ионизации все величины рассчитываются численно, для чего их удобно выразить через производные

$%\begin{displaymath}\left( \frac{\partial \ln P}{\partial \ln\rho }\right) _{T} ,~ \left( \frac{\partial \ln P}{\partial \ln T}\right) _{\rho },~ %\left( \frac{\partial S}{\partial \ln\rho }\right) _{T} ,~ \left( \frac{\partial S}{\partial \ln T}\right) _{\rho }=c_{\upsilon }. \end{displaymath} \left(\partial\ln P\over \partial\ln\rho \right)_T,\quad \left(\partial\ln P\over \partial\ln T \right)_\rho,\quad \left(\partial S\over \partial\ln\rho\right)_T, \quad \left(\partial S\over \partial\ln T\right)_\rho=c_v.$

Воспользуемся известными свойствами якобианов

$%\begin{displaymath}\frac{\partial (u,\upsilon )}{\partial (x,y)}=\frac{\partial (u,\upsilon )}{\partial (t,s)}\frac{\partial (t,s)}{\partial (x,y)} ; \quad %\frac{\partial (u,\upsilon )}{\partial (x,\upsilon )}=\left( \frac{\partial u}{\partial x}\right) _{\upsilon }. \end{displaymath} {\partial (u,v)\over \partial (x,y)} = {\partial (u,v)\over \partial (t,s)}{\partial (t,s)\over \partial (x,y)};\quad {\partial (u,v)\over \partial (x,v)} = \left(\partial u\over \partial x\right)_v,$

(1.10)

Получаем

$%\begin{displaymath}\gamma _{1}=\left( \frac{\partial \ln P}{\partial \ln\rho }\right) _{T}-\left( \frac{\partial \ln P}{\partial \ln T}\right) _{\rho }\left( \frac{\partial S}{\partial \ln\rho }\right) _{T}\left/\left( \frac{\partial S}{\partial \ln T}\right)\right. _{\rho } , \end{displaymath} \gamma_1=\left(\partial\ln P\over \partial\ln\rho \right)_T- \left(\partial\ln P\over \partial\ln T \right)_\rho \left(\partial S\over \partial\ln\rho\right)_T \bigg/ \left(\partial S\over \partial\ln T\right)_\rho,$

(1.11)

$%\begin{displaymath}\gamma _{2}=\left[ \left( \frac{\partial \ln P}{\partial \ln T}\right) _{\rho }-\left( \frac{\partial \ln P}{\partial \ln\rho }\right) _{T}\left( \frac{\partial S}{\partial \ln T}\right) _{\rho }\left/\left( \frac{\partial S}{\partial \ln\rho }\right)\right. _{T}\right] ^{-1}, \end{displaymath} \gamma_2=\left[\left(\partial\ln P\over \partial\ln T\right)_\rho- \left(\partial\ln P\over \partial\ln\rho \right)_T \left(\partial S\over \partial\ln T\right)_\rho \bigg/ \left(\partial S\over \partial\ln\rho\right)_T\right]^{-1},$

(1.12)

$%\begin{displaymath}\gamma _{3}=-\left( \frac{\partial S}{\partial \ln\rho }\right) _{T}\left/\left( \frac{\partial S}{\partial \ln T}\right)\right. _{\rho }, \end{displaymath} \gamma_3= -\left(\partial S\over \partial\ln\rho\right)_T \bigg/ \left(\partial S\over \partial\ln T\right)_\rho,$

(1.13)

$%\begin{displaymath}c_{\upsilon }=(\partial S/\partial \ln T)_{\rho }, \end{displaymath} c_v=\left(\partial S/\partial \ln T \right)_\rho,$

(1.14)

$%\begin{displaymath}c_{p}=c_{\upsilon }-\left( \frac{\partial S}{\partial \ln\rho }\right) _{T}\left( \frac{\partial \ln P}{\partial \ln T}\right) _{\rho }\left/\left( \frac{\partial \ln P}{\partial \ln\rho }\right)\right. _{T}, \end{displaymath} c_p=c_v-\left(\partial S\over \partial\ln\rho\right)_T \left(\partial\ln P\over \partial\ln T \right)_\rho \bigg/ \left(\partial \ln P\over \partial\ln\rho\right)_T,$

(1.15)

$%\begin{displaymath}c_{p}/c_{\upsilon }=\gamma \left/\left( \frac{\partial \ln P}{\partial \ln\rho }\right)\right. _{T}. \end{displaymath} c_p/c_v=\gamma_1 \bigg/ \left(\partial \ln P\over \partial\ln\rho\right)_T.$

(1.16)

Производные от энтропии выражаются через производные от энергии и давления из первого закона термодинамики и условия полноты дифференциала свободной энергии $F=E-TS$ :

$%\begin{displaymath} %\left( \frac{\partial S}{\partial \ln T}\right) _{\rho }=\frac{1}{T}\left( \frac{\partial E}{\partial \ln T}\right) _{\rho }, \quad %\left( \frac{\partial S}{\partial \ln \rho }\right) _{T}=-\frac{1}{\rho T}\left( \frac{\partial P}{\partial \ln T}\right) _{T}. %\end{displaymath} \left(\partial S\over \partial\ln T\right)_\rho= {1\over T}\left(\partial E\over \partial\ln T\right)_\rho,\quad \left(\partial S\over \partial\ln\rho \right)_T= -{1\over\rho T}\left(\partial P\over \partial\ln T\right)_\rho.$

(1.17)

Если степени ионизации $y_{ij}$ постоянны, то из (1.3)-(1.6) следeдует

$%\begin{displaymath}S=\frac{k}{\mu m_{u}}\ln \left( T^{3/2}/\rho \right) +\frac{4}{3}\frac{aT^{3}}{\rho }+const \end{displaymath} S={k\over \mu m_{\rm u}}\ln(T^{3/2}/\rho)+{4\over 3}{aT^3\over\rho} +{\rm const}$

(1.18)

и все производные вычисляются аналитически:

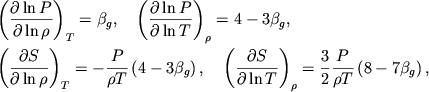$%\begin{displaymath} %\hbox{% %\begin{tabular}{ll} %$\displaystyle{ \left( \frac{\partial \ln P}{\partial \ln \rho }\right) _{T}=\beta _{g}, }$ & %$\displaystyle{ \left( \frac{\partial \ln P}{\partial \ln T}\right) _{\rho }=4-3\beta _{g}, }$ \\ %$\displaystyle{ \left( \frac{\partial S}{\partial \ln \rho }\right) _{T}=-\frac{P}{\rho T}\left( 4-3\beta _{g}\right), }$ & %$\displaystyle{ \left( \frac{\partial S}{\partial \ln T}\right) _{\rho }=\frac{3}{2}\frac{P}{\rho T}\left( 8-7\beta _{g}\right). }$ \\ %\end{tabular}} %\end{displaymath} \eqalign{ %(1.19) &\left(\partial \ln P\over \partial\ln\rho\right)_T=\beta_g, \quad \left(\partial \ln P\over \partial\ln T\right)_\rho=4-3 \beta_g, \cr &\left(\partial S\over \partial\ln \rho\right)_T=-{P\over\rho T} \left(4-3 \beta_g\right), \quad \left(\partial S\over \partial\ln T\right)_\rho= {3\over 2}{P\over\rho T}\left(8-7 \beta_g\right), \cr}$

(1.19)

Здесь $\beta _{g}=P_{g}/P$ - отношение газового давления к полному. Выражения для адиабатических показателей и теплоемкостей одноатомного газа с $\mu =const$ и излучения принимают вид [218]

$\eqalign{ &\gamma_1=\beta_g +{2\over 3}{\left(4-3 \beta_g\right)^2\over 8-7 \beta_g}, \quad \gamma_2=\left[4-3\beta_g+{3\over 2}\beta_g{8-7\beta_g\over 4-3\beta_g} \right]^{-1},\cr &\gamma_3={2\over 3}{4-3 \beta_g\over 8-7 \beta_g}, \cr &c_v={3\over 2}{P\over\rho T}\left(8-7 \beta_g\right), \cr &c_p={3\over 2}{P\over\rho T}\left(8-7 \beta_g\right) \left[1+{2\over 3}{\left(4-3 \beta_g\right)^2\over\beta_g \left(8-7 \beta_g\right)}\right], \cr &{c_p\over c_v}=1+{2\over 3}{\left(4-3 \beta_g\right)^2\over\beta_g \left(8-7 \beta_g\right)}=\gamma_1/\beta_g. \cr}$

(1.20)

Соотношения (1.18)-(1.20) широко применяются при описании звезд ной материи, так как основная часть массы звезд находится в состоянии полной ионизации с $\mu =const$ . В оболочках звезд, где температура меньше, вещество ионизовано не полностью и $\mu =\mu \left( \rho ,T\right)$ .

Задача. Вывести уравнения для концентраций электронов в плазме, состоящей из $H^{0},$ $H^{+},$ $H^{-}$ , $He^{0},$ $He^{+},$ $He^{++}$ , а также атомов и однократно ионизованных ионов $k$ других элементов.

Решение. Используя формулу Саха (1.8) и табл. 2, получаем для водорода

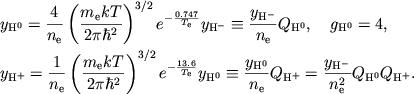$\eqalign{ &y_{\rm H^0}={4\over n_{\rm e}}\left(m_{\rm e}kT \over 2\pi\hbar^2 \right)^{3/2}e^{-{0.747 \over T_{\rm e}}} y_{\rm H^-}\equiv {y_{\rm H^-} \over n_{\rm e}}Q_{\rm H^0}, \quad g_{\rm H^0}=4, \cr &y_{\rm H^+}={1\over n_{\rm e}}\left(m_{\rm e}kT \over 2\pi\hbar^2 \right)^{3/2}e^{-{13.6 \over T_{\rm e}}} y_{\rm H^0}\equiv {y_{\rm H^0} \over n_{\rm e}}Q_{\rm H^+}= {y_{\rm H^-} \over n_{\rm e}^2}Q_{\rm H^0}Q_{\rm H^+}. \cr}$

(1)

$\begin{displaymath}y_{H^{+}}=\frac{1}{n_{e}}\left( \frac{m_{e}kT}{2\pi h^{2}}\right) ^{3/2}e^{-\frac{13.6}{T_{\mbox{э}}}}y_{H^{0}}\equiv \frac{y_{H^{0}}}{n_{e}}Q_{H^{+}}=\frac{y_{H^{-}}}{n_{e}^{2}}Q_{H^{0}}Q_{H^{+.}} \end{displaymath}$

Используя условие $%$ y_{H^{-}}+y_{H^{0}}+y_{H^{+}}=1 $ y_{\rm H^-}+y_{\rm H^0}+y_{\rm H^+}=1$ , имеем

$%\begin{displaymath}y_{H^{-}}=n_{e}^{2}\left( n_{e}^{2}+n_{e}Q_{H^{0}}+Q_{H^{0}}Q_{H^{+}}\right) ^{-1} \end{displaymath} y_{\rm H^-}=n_{\rm e}^2\left(n_{\rm e}^2+n_{\rm e}Q_{\rm H^0}+ Q_{\rm H^0}Q_{\rm H^+}\right)^{-1}$

(2)

Аналогично для гелия получаем

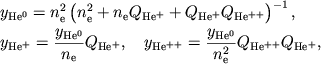$\eqalign{ &y_{\rm He^0}=n_{\rm e}^2\left(n_{\rm e}^2+n_{\rm e}Q_{\rm He^+}+ Q_{\rm He^+}Q_{\rm He^{++}}\right)^{-1}, \cr &y_{\rm He^+}={y_{\rm He^0} \over n_{\rm e}}Q_{\rm He^+}, \quad y_{\rm He^{++}}={y_{\rm He^0} \over n_{\rm e}^2} Q_{\rm He^{++}}Q_{\rm He^+}, \cr}$

(3)

где

$%\begin{displaymath} %Q_{He^{+}}=4\left( \frac{m_{e}kT}{2\pi h^{2}}\right) ^{3/2}e^{-\frac{24.6}{T_{\mbox{э}}}}, \quad %Q_{He^{++}}=\left( \frac{m_{e}kT}{2\pi h^{2}}\right) ^{3/2}e^{-\frac{54.4}{T_{\mbox{э}}}} %\end{displaymath} Q_{\rm He^+}=4\left(m_{\rm e}kT \over 2\pi\hbar^2 \right)^{3/2}e^{-{24.6 \over T_{\rm e}}}, \quad Q_{\rm He^{++}}=\left(m_{\rm e}kT \over 2\pi\hbar^2 \right)^{3/2}e^{-{54.4 \over T_{\rm e}}}$

(4)

и для тяжелых элементов

$%\begin{displaymath} %y_{j^{+}}=\frac{Q_{j^{+}}}{n_{e}+Q_{j^{+}}} , \quad %Q_{j^{+}}=2\frac{g_{j^{+}}}{q_{j^{0}}}\left( \frac{m_{e}kT}{2\pi \hbar ^{2}}\right) ^{3/2}e^{-\frac{I_{j1}}{kT}} . %\end{displaymath} y_{j^+}={Q_{j^+}\over n_{\rm e}+ Q_{j^+}}, \quad Q_{j^+}=2{g_{j^+} \over g_{j^0}}\left(m_{\rm e}kT \over 2\pi\hbar^2 \right)^{3/2}e^{-{I_{j1} \over kT}}.$

(5)

Здесь $T_{\mbox{э}}$ температура в электронвольтах. Используя соотношение (4) для каждого элемента и условие электронейтральности (5)

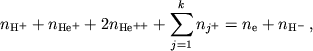
$%$ n_{H^{+}}+n_{He^{+}}+2n_{He^{++}}+\sum _{j=1}^{k}n_{j^{+}}=n_{e}+n_{H^{-}} $ n_{\rm H^+}+n_{\rm He^+}+2n_{\rm He^{++}}+\sum_{j=1}^kn_{j^+}= n_{\rm e}+n_{\rm H^-}\,,$

получаем уравнение для приведенной электронной концентрации

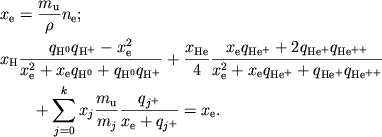$%\begin{displaymath} %\hbox{ %\begin{tabular}{l} %$\displaystyle{ x_{e}=\frac{m_{u}}{\rho }n_{e} , }$ %$\displaystyle{ x_{H}\frac{q_{_{^{H^{0}}}}q_{_{^{H^{+}}}}-x_{e}^{2}}{x^{2}_{e}+x_{e}q_{_{^{H^{0}}}}+q_{_{^{H^{0}}}}q_{_{^{j^{+}}}}}+\frac{x_{He}}{4}\frac{x_{e}q_{_{^{He^{+}}}}+2q_{_{^{He^{+}}}}q_{_{^{He^{++}}}}}{x_{e}^{2}+x_{e}q_{_{^{He^{+}}}}+q_{_{^{He^{+}}}}q_{_{^{He^{++}}}}}+ }$ %$\displaystyle{ \qquad\qquad + \Sigma _{j=0}^{k}\frac{m_{u}}{m_{j}}\frac{q_{_{^{j^{+}}}}}{x_{e}+q_{_{^{j^{+}}}}}=x_{e} . }$ %\end{tabular}} %\end{displaymath} \eqalign{ &x_{\rm e}= {m_{\rm u}\over \rho} n_{\rm e}; \cr &x_{\rm H}{q_{\rm H^0}q_{\rm H^+}-x_{\rm e}^2 \over x_{\rm e}^2+x_{\rm e}q_{\rm H^0}+q_{\rm H^0}q_{\rm H^+}}+ {x_{\rm He} \over 4} {x_{\rm e}q_{\rm He^+}+2q_{\rm He^+}q_{\rm He^{++}} \over x_{\rm e}^2+x_{\rm e}q_{\rm He^+}+q_{\rm He^+}q_{\rm He^{++}}} \cr &\qquad+\sum_{j=0}^k x_j{m_{\rm u} \over m_j} {q_{j^+} \over x_{\rm e}+q_{j^+}} = x_{\rm e}. \cr}$

(6)

Здесь $q_{i}=m_{u}Q_{i}/\rho$ . Все величины в (6) безразмерны и близки к единице, что удобно для численного решения.

После нахождения степеней ионизации в зависимости от $\rho$ и $T$ , можно вычислить термодинамические функции и их производные. На рис. 1 в качестве примера такого расчета приведена зависимость $\gamma _{3}(\rho ,T)$ для смеси с составом $x_{H}=0.75$ , $x_{He}=0.22$ х и солнечным соотношением между другими элементами (табл. 1). Два минимума на кривых $\gamma _{3}\left\vert _{\rho }(T)\right.$ соответствуют областям ионизации водорода и первой ионизации гелия. При малой плотности $\rho =10^{-12}\mbox{~г}\cdot \mbox{см}^{-3}$ второй минимум попадает в область преобладания давления излучения и потому не заметен.

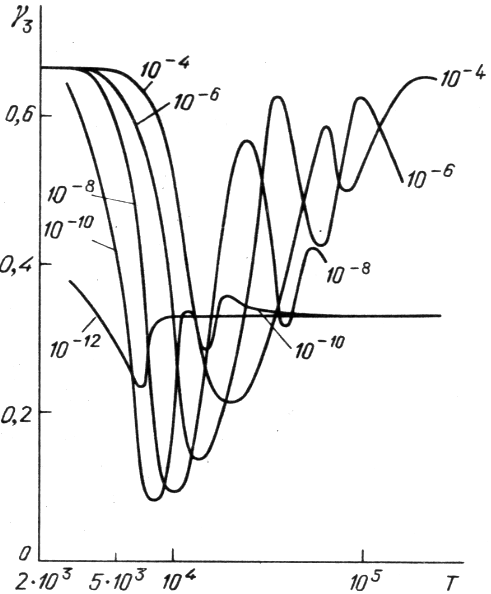Рис. 1. Зависимости $\gamma(T)$ при $\rho$ = const, указанных на кривых, для нормального состава (табл. 1) в области, где происходит ионизация водорода и гелия

<< Предисловие | Оглавление | 2. Релятивистский газ с вырождением >>

Публикации с ключевыми словами: Эволюция звезд - физические процессы
Публикации со словами: Эволюция звезд - физические процессы

См. также:

Переработка вещества в Кассиопее А

NGC 7789: Роза Каролины

Планетарная туманность NGC 2818 от Хаббла

Научная конференция "Наблюдаемые проявления эволюции звезд" в САО РАН

Планетарные туманности

Прошлые и будущие звёзды Андромеды

Туманность Ожерелье

Все публикации на ту же тему >>

Обсудить эту публикацию

Версия для печати

Астрометрия - Астрономические инструменты - Астрономическое образование - Астрофизика - История астрономии - Космонавтика, исследование космоса - Любительская астрономия - Планеты и Солнечная система - Солнце