2.3 Контуры спектральных линий
Вопрос о контурах спектральных линий, образованных движущимися атмосферами звезд, рассматривался в работах многих авторов. Во всех этих работах предполагалось, что темные компоненты ярких линий возникают в обращающем слое, находящемся ниже прозрачной оболочки, в которой образуются яркие линии. Однако в предыдущем параграфе было показано, что такой взгляд является неправильным. На самом деле как темные, так и яркие линии возникают в одном и том же протяженном обращающем слое. Поэтому необходимо дать теорию контуров спектральных линий, основанную на этой новой точке зрения.
Вообще говоря, вопрос о нахождении контуров линий для движущихся оболочек является гораздо более сложным чем для неподвижных. Однако в том предельном случае, когда скорость движения оболочки значительно превосходит среднюю термическую скорость атомов, контуры линий могут быть вычислены весьма легко. Это происходит оттого, что в этом случае можно пренебречь всеми факторами, влияющими на контур линии, кроме одного - движения оболочки. И только в этом случае может быть достаточно уверенно решена и обратная задача - нахождение по контурам линий параметров, определяющих движение оболочки. Можно считать, что указанный случай в очень хорошем приближении осуществляется в оболочках звезд типов WR, P Cygni, Be и Новых. Именно этот случай мы и рассматриваем в настоящем параграфе.
Для простоты мы считаем, что имеется резкая граница между фотосферой и атмосферой звезды. В отличие от обычной терминологии под линией поглощения мы понимаем линию, образованную поглощением света, идущего от фотосферы, в атмосфере звезды, а под линией излучения - линию, образованную излучением света самой атмосферой (с учетом самообращения). Наложение второй линии на первую дает наблюдаемую спектральную линию.
Ясно, что вычисление контуров линий поглощения (в нашем смысле) не вызывает затруднений. Для этого для каждой частоты ν надо найти соответствующую поверхность равных лучевых скоростей. Часть этой поверхности, находящаяся в обращающем слое, закрывает от наблюдателя некоторую часть диска звезды. Оставшаяся открытой часть диска звезды дает остаточную интенсивность линии поглощения в частоте ν.
Чтобы вычислить контур линии излучения, надо для каждой частоты найти яркость соответствующей поверхности равных лучевых скоростей (ибо в отличие от случая прозрачной оболочки, когда излучает объем, в случае непрозрачной оболочки, грубо говоря, излучает поверхность). Для этого необходимо определить интенсивность излучения, выходящего (вследствие эффекта Доплера) из каждого места атмосферы. Обозначая через Jik(r) интенсивность излучения, соответствующего переходу k → i, выходящего из атмосферы на расстоянии r от центра звезды, мы, очевидно, имеем
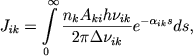
|
(26) |
или, производя интегрирование:
|
|
(27) |
Величины ![]() в виде функций от r должна дать теория лучевого равновесия движущейся среды. В качестве такой теории можно использовать результаты, полученные нами ранее.
в виде функций от r должна дать теория лучевого равновесия движущейся среды. В качестве такой теории можно использовать результаты, полученные нами ранее.
Основываясь на изложенных соображениях, мы в этом, параграфе вычисляем контуры спектральных линий отдельно для двух случаев: а) для звезд типов WR, P Cygni и Новых (т.е. для случая истечения материи из звезд) и б) для звезд, типа Be (т.е. для случая истечения материи из быстро вращающихся звезд).
a)Звезды типов WR, P Cygni и Новые
Как известно, в спектрах Новых до максимума блеска видны абсорбционные линии, сильно смещенные в фиолетовую сторону, без заметных следов эмиссии. После максимума появляются яркие линии, ограниченные с фиолетовой стороны абсорбционными спутниками. Подобный же вид имеют линии в спектрах звезд типов WR и Р Cygni. Такой характер спектра говорит о непрерывном истечении материи из звезд типов WR и Р Cygni и о выбрасывании оболочек при возгорании Новых. Для выяснения всех особенностей движения материи, выбрасываемой из звезд, необходим подробный анализ контуров спектральных линий.
В теоретических работах других авторов контуры вычислялись отдельно для темных и для ярких линий. Для получения контуров абсорбционных линий, образованных движущейся атмосферой, обычно брались контуры линий, образованных неподвижной атмосферой, и определялась деформация этих контуров, происходящая оттого, что разные части атмосферы имеют разную скорость по отношению к наблюдателю. Таковы работы Carroll [5], Герасимовича и Мельникова [6], Wilson [7], Воронцова-Вельяминова [8] и др., ставившие своей целью объяснение контуров абсорбционных линий в спектрах Новых перед максимумом блеска. Однако все эти работы имеют тот недостаток, что в них все дело сводится к "наблюдаемому" эффекту Доплера, в то время как в действительности необходимо ввести эффект Доплера в уравнения переноса излучения. Впервые такая попытка (точнее говоря, попытка решения проблемы Шустера при учете эффекта Доплера), была предпринята Мс Сгеа и Mitra [9]. Совсем недавно рассмотрением этой проблемы занимался Chandrasekhar [10]. Однако в этих работах не учитывалось изменение частоты светового кванта, происходящее при элементарном акте рассеяния, вследствие эффекта Допплера, обусловленного тепловым движением атомов. Контуры линий, вычисленные в перечисленных работах, оказались мало похожими на наблюденные. Это объясняется не только неточностью учета движения оболочки, но также тем, что не была принята во внимание большая протяженность обращающего слоя, характерная для рассматриваемых звезд.
При нахождении контуров эмиссионных линий в работах других авторов предполагалось, что атмосфера звезды полностью прозрачна для излучения в линиях. Впервые этим вопросом занимался Beals [11], показавший, что эмиссионные линии, образованные оболочкой, состоящей из атомов, движущихся с постоянной скоростью в радиальном направлении, должны иметь прямоугольные контуры. Однако контуры эмиссионных линий в спектрах звезд типа WR и Новых являются, как правило, закругленными. Вследствие этого появилась мысль, что атомы, образующие оболочку, движутся не с постоянной скоростью, а ускоренно или замедленно. Контуры линий излучения для этих случаев определены в работах Герасимовича [12], Chandrasekhar [13] и Wilson [7] . Совершенно очевидно, что при подходящем выборе градиента скорости можно получить любой симметричный контур.
На самом деле, как уже сказано, надо считать, что как темные, так и яркие линии возникают в одном и том же протяженном обращающем слое. Приступая к нахождению контуров линий, возникающих в таком слое, мы для простоты допустим, что из звезды происходит истечение материи со скоростью v, не меняющейся с расстоянием. Найдем сначала контуры линий поглощения (в нашем смысле).
Пусть r0 и r1 - соответственно нижняя и верхняя границы обращающего слоя. Атомы, движущиеся в атмосфере под углом θ к наблюдателю, поглощают излучение, идущее от фотосферы, частота которого равна
|
|
(28) |
Эти атомы экранируют кольцеобразную часть диска звезды, заключенную между углами θ и θ1, где θ1 определяется условием:
|
|
(29) |
Следовательно, отношение интенсивности частоты ν в спектральной линии к интенсивности соседнего места в непрерывном спектре будет равно
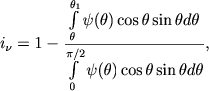
|
(30) |
где ψ (θ) есть закон потемнения диска от центра к краю. Этой формулой и определяется контур линии поглощения.
Для функции ψ (θ) мы не можем взять ее обычное выражение, так как рассматриваемые звезды обладают протяженными фотосферами, что приводит к более сильному потемнению диска при переходе от центра к краю, чем для обычных звезд. Поэтому функцию ψ (θ) мы берем в виде
|
|
(31) |
где a, b, n - некоторые параметры.
Легко видеть, что нахождение контуров линий поглощения для разных ![]() сводится к нахождению контуров для r1 = ∞ , т.е. для θ1 = π/2. В последнем же случае, подставляя (31) в (30) и интегрируя, мы находим
сводится к нахождению контуров для r1 = ∞ , т.е. для θ1 = π/2. В последнем же случае, подставляя (31) в (30) и интегрируя, мы находим
|
|
(32) |
где вместо частоты ν введена величина y, связанная с частотой соотношением
|
|
(33) |
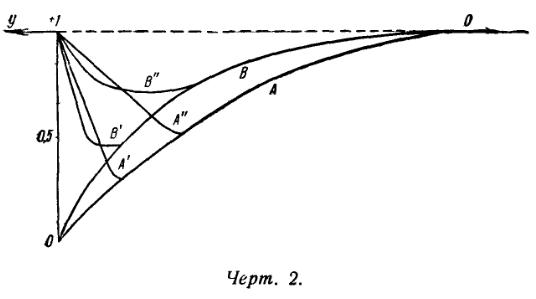
Контуры линий поглощения, вычисленные по вышеперечисленным формулам, для двух законов потемнения:
|
|
(34) |
даны на черт. 2. Контуры, полученные для случая r1=∞ , обозначены буквами A и B. Буквами A'v, B' и A", B" отмечены контуры, вычисляемые для двух следующих случаев: ![]() .
.
Перейдем теперь к нахождению контуров линии излучения. Для нахождения энергии частоты ν, излучаемой атмосферой, надо проинтегрировать интенсивность излучения, выходящего из атмосферы, по соответствующей поверхности равных лучевых скоростей. В данном случае эта поверхность является конусом с вершиной в центре звезды и осью, направленной к наблюдателю. Поэтому для искомой энергии мы получаем
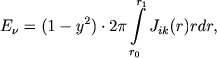
|
(35) |
где интенсивность Jik(r) определяется равенством (27). Таким образом, в случае истечения материи с постоянной скоростью, контур линии излучения оказывается параболическим (обозначен буквой С на черт. 3).
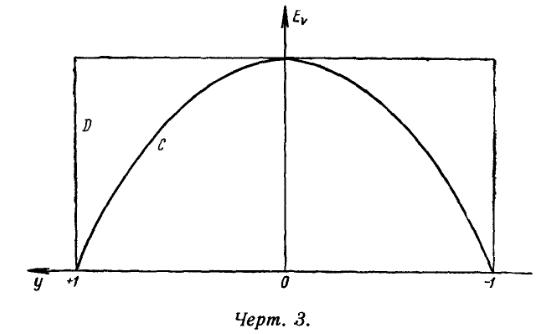
Чтобы получить контур спектральной линии, надо наложить линию излучения на линию поглощения (примеры контуров которых даны на черт. 2). При этом оказываются возможными три случая [в зависимости главным образом от значения интеграла в формуле (35)]:
- Вообще говоря, получаются яркие линии с темными компонентами на фиолетовой стороне, т. е. линии такого же, вида, как в спектрах звезд типов Р Cygni, WR и Новых. Следует отметить, что параболический контур яркой линии оказывается гораздо ближе к наблюдаемым, чем прямоугольный контур D, полученный Beals для прозрачных оболочек.
- Если линия поглощения слаба, а линия излучения, наоборот, сильна, то вторая из них может "заполнить" первую, и мы увидим одну только линию излучения. Такой случай часто осуществляется в спектрах звезд типа WR (при этом играет также некоторую роль влияние излучения прозрачной части оболочки, дающего контур типа D). Именно поэтому эмиссионные линии в спектрах этих звезд оказываются асимметричными и "смещенными" в красную сторону спектра. Для объяснения этого "красного смещения" Wilson [15] предположил наличие гравитационного эффекта. Мы видим, однако, что в такой гипотезе нет необходимости.
- Если линия поглощения сильна, а линия излучения, наоборот, слаба, то мы увидим одну только линию поглощения (в обычном смысле). Остаточная интенсивность в линии создается при этом не светом, рассеянным атмосферой, а фотосферным излучением, не экранированным движущимися атомами. Такой случай имеет место в спектрах новых звезд перед максимумом блеска. Как известно, эти линии являются резкими и узкими (причем ширина линии значительно меньше ее смещения). Именно такого рода линии изображены на черт. 2. Из этого чертежа видно, что линия тем резче, чем больше толщина обращающего слоя, и тем уже, чем больше потемнение диска от центра к краю. Отметим, что в ранних работах, посвященных теоретическому определению контуров линий поглощения в спектрах новых звезд, принималось, что толщина обращающего слоя мала, а закон потемнения диска к краю имеет обычную форму. Вычисленные при этих предположениях контуры получались широкими и неглубокими. Впервые на важность сильного потемнения диска к краю обратил внимание Б. А. Воронцов-Вельяминов [8], а на важность большой протяженности обращающего слоя - Э. Р. Мустель [14]. В действительности, как мы видим, важны обе эти причины.
б) Звезды типа Be
Как правило, в спектрах звезд типа Be яркие лини накладываются на широкие и неглубокие полосы поглощения. В свою очередь на яркие линии накладываются узкие линии поглощения, разделяя их на два компонента. Однако в некоторых спектрах яркие линии являются одиночными, в других спектрах - как одиночными, так и двойными.
По-видимому, все Ве-звезды являются "звездами с переменными спектрами". В одних случаях происходит изменение полной интенсивности ярких линий, а иногда их появление и исчезновение (Плейона, μ Центавра и др.), в других - периодически меняется отношение интенсивностей двух компонентов каждой эмиссионной линии (причем иногда красный компонент ярче, иногда фиолетовый). Для звезд второй группы (их называют "звездами типа φ Persei") замечены следующие закономерности. С изменением интенсивностей компонентов связано изменение смещения линий. Когда красный компонент сильнее, эмиссионная линия и ее центральная абсорбция смещены в фиолетовую сторону спектра. Когда фиолетовый компонент сильнее, эти линии смещены в красную сторону спектра. Когда эмиссионные компоненты не равны, широкая полоса поглощения сильнее выступает на стороне более сильного компонента.
Для объяснения контуров линий в спектрах звезд типа Be Otto Struve [15] высказал гипотезу, согласно которой полосы поглощения образуются в обращающем слое быстро вращающейся звезды, а раздвоенные яркие линии - в прозрачном газовом кольце, вращающемся вокруг звезды. Однако для объяснения всех особенностей таких спектров гипотеза Struve недостаточна. Необходимо также допустить наличие процесса истечения материи, носящего переменный характер. С другой стороны, по мнению Me Laughlin [16], указанные выше изменения в спектрах звезд типа φ Persei можно объяснить предположением о пульсации вращающейся звезды.
Таким образом оболочки звезд типа Be участвуют, по-видимому, в двух видах движения - вращательном и радиальном. Возникает поэтому задача о нахождении контуров спектральных линий, образованных такой оболочкой. Struve рассмотрел эту задачу для прозрачного вращающегося кольца. Однако представляет интерес решение той же задачи для более общего случая (вращение плюс радиальное движение) при непрозрачности оболочки для излучения в линиях.
Мы вычислим сейчас контуры линий, образованных вращающейся и расширяющейся оболочкой, для предельного случая, указанного выше (v >> u). При этом мы снова будем считать, что скорость расширения одинакова для всех слоев. Что же касается скорости вращения, то мы примем, что эта скорость убывает обратно пропорционально расстоянию от центра звезды, т. е. имеет место сохранение углового момента.
Рассмотрим для простоты экваториальную плоскость звезды. Пусть ![]() усть скорость вращения и
усть скорость вращения и ![]() - скорость расширения атмосферы. Тогда лучевая скорость будет равна
- скорость расширения атмосферы. Тогда лучевая скорость будет равна
|
|
(36) |
где ![]() .
.
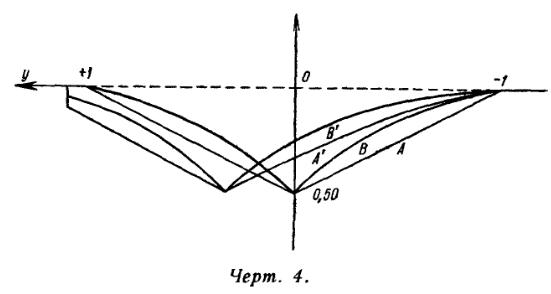
Контуры линий поглощения, вычисленные нами для двух случаев: k = 0 ("чистое" вращение) и k = 1/3 для двух законов потемнения (34), даны на черт. 4 [при этом величина y снова определяется соотношением (33), в котором под v теперь понимается скорость v'(r0)].
Найдем теперь контуры линий излучения. Пусть Eν есть количество энергии частоты ν, излучаемой экваториальным слоем в единичном телесном угле. Для этой величины мы находим
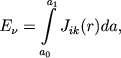
|
(37) |
где ![]() , a пределы интегрирования определяются из соотношений:
, a пределы интегрирования определяются из соотношений:
|
|
(38) |
|
|
(39) |
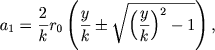
|
(40) |
причем берется одно из соотношений (39) или (40), в зависимости от того, пересекаются кривые равных лучевых скоростей с окружностью радиуса r1 или нет Величина же Jik(r) как и раньше, определяется формулой (27).
Для вычисления интеграла (37) надо знать зависимость величин ![]() от радиуса, для чего для данного случая необходимо выразить параметр x, от которого отношение
от радиуса, для чего для данного случая необходимо выразить параметр x, от которого отношение ![]() зависит, в виде функции от r (см. предыдущий параграф). Для простоты мы положим Jik = const. Тогда вместо (37) получаем
зависит, в виде функции от r (см. предыдущий параграф). Для простоты мы положим Jik = const. Тогда вместо (37) получаем
|
|
(41) |
Для случая чистого вращения эта формула приводится к виду:
![$$
\left. \begin{array}{lr} E_\nu = J_{ik} r_0 y\left[\left(\frac{r_1}{r_0}\right)^2 - 1\right],& \qquad \mbox{если} |y| < \frac{r_0}{r_1} \\
E_\nu = J_{ik} r_0 y\left[\frac{1}{y^2} - 1 \right],& \qquad \mbox{если} |y| > \frac{r_0}{r_1}
\end{array} \right\} $$](https://images.astronet.ru/pubd/2011/06/28/0001252608/tex/formula211.gif)
|
(42) |
Контуры линий излучения, вычисленные по формулам (41) и (42) для случаев: ![]() , приведены на черт. 5. Эти линии должны быть наложены на линии поглощения, примеры которых даны на черт. 4.
, приведены на черт. 5. Эти линии должны быть наложены на линии поглощения, примеры которых даны на черт. 4.
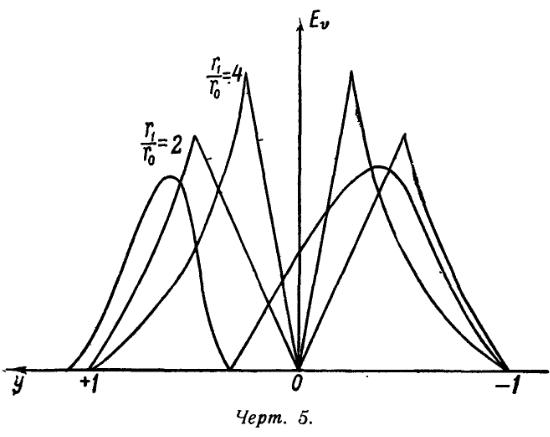
Из рассмотрения приведенных формул и чертежей можно сделать следующие выводы:
- Вообще говоря, вычисленные контуры весьма похожи на контуры линий в спектрах звезд типа Be. В случае чистого вращения оба компонента ярких линий оказываются одинаковыми, в случае вращения и расширения - яркие линии смещены в фиолетовую сторону спектра, и фиолетовый компонент слабее красного. Именно последнего рода линии чаще встречаются в спектрах звезд типа Be. Указанный факт свидетельствует об истечении материи из этих звезд.
- Если бы мы рассмотрели вращающуюся и сжимающуюся атмосферу, то получили бы яркие линии, смещенные в красную сторону спектра, и красный компонент оказался бы слабее фиолетового. Такие контуры, вместе с полученными выше для вращающейся и расширяющейся атмосферы, подтверждают гипотезу Mc Laughlin о пульсации вращающихся атмосфер в случае звезд типа φ Persei.
- Вычисленные яркие линии оказываются, вообще говоря, двойными. Однако расстояние между компонентами тем меньше, чем меньше скорость вращения звезды и чем больше величина r1/r0. Поэтому в спектрах некоторых звезд компоненты должны сливаться, и мы увидим одиночные линии. В спектрах же других звезд могут наблюдаться как одиночные, так и раздвоенные линии (ибо для разных линий величины - различны). Этим, по-видимому, объясняются различия в форме ярких линий в спектрах звезд типа Be.
- В случае протяженного обращающего слоя полная интенсивность линии поглощения возрастает с увеличением скорости вращения звезды. Этот факт должен быть отмечен потому, что в обычном случае полная интенсивность абсорбционной линии не меняется при расширении линии, вследствие вращения звезды.
Мы видим, что предложенная теория контуров спектральных линий в спектрах звезд типов WR, P Cygni и Be, несмотря на ее элементарный характер, находится в хорошем согласии с наблюдениями. Это говорит как в пользу принятых представлений о движении в звездных атмосферах, так и в пользу нашей точки зрения о возникновении как ярких, так и темных линий в одной и той же протяженной оболочке. Нам кажется, что в дальнейшем представит интерес применение результатов, полученных в этой главе, к изучению атмосфер конкретных звезд (например P Cygni, γ Cassiopeiae и др.). Благодаря простоте полученных результатов при этом не встретится особых трудностей.
<< 2.2 Изменение возбуждения вдоль радиуса | Оглавление | Глава III. Газовые туманности >>
|
Публикации с ключевыми словами:
оболочки звезд - перенос излучения
Публикации со словами: оболочки звезд - перенос излучения | |
|
См. также:
| |