1.4 О прозрачности среды для излучения в линиях
Как было выяснено, с увеличением параметра х степень возбуждения быстро убывает, и при достаточно больших значениях х среда становится прозрачной для излучения в линиях всех серий, начиная c j+1-й. Условием непрозрачности среды в линиях j-й серии является выполнение неравенства βjk < 1. Однако заранее мы не можем сказать, начиная с какой серии среда будет прозрачной, так как величины βjk зависят от величин nj являющихся неизвестными. Желательно поэтому иметь простой способ оценки чисел nj.
Сейчас мы дадим приближенный метод решения системы (9), основанный на том обстоятельстве, что при больших значениях х числа nj быстро убывают с возрастанием номера j.
Складывая почленно все уравнения (9), начиная с j-го, получаем
![\begin{eqnarray} \sum_{i=j}^{\infty} n_i\left[x\sum_{k=1}^{j-1} \frac{\frac{g_2}{g_1}n_1-n_2}{\frac{g_i}{g_k}n_k-n_i}\left(\frac{\nu_{ki}}{\nu_{12}}\right)^3+\frac{B_{ic}\rho_{ic}^*}{A_{21}}\right]=\frac{n_e n^+}{WA_{21}}\sum_{i=j}^{\infty} C_i,\nonumber
\end{eqnarray}](https://images.astronet.ru/pubd/2011/06/28/0001252608/tex/formula172.gif)
|
(21) |
Пренебрегая эйнштейновским отрицательным поглощением и обозначая
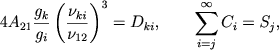
|
(22) |
вместо (21) находим
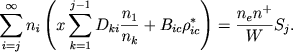
|
(23) |
Принимая во внимание убывание чисел ni и Dki с возрастанием i, ограничимся в суммировании по i одним первым членом. Тогда получаем
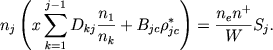
|
(24) |
Мы пришли к рекурентной формуле, дающей число nj, если известны числа n1, n2,... nj-1.
Для j=1 мы можем взять более точную формулу, чем та, которая следует из (24), а именно:
|
|
(25) |
Тогда уравнение (25) и второе из уравнений (24) дают
|
|
(26) |
где ![]() . Привлекая следующее из уравнений (24), получаем
. Привлекая следующее из уравнений (24), получаем
|
|
(27) |
И так далее.
Если при вычислении по формулам (24) мы получим такое число nj, что окажется βjk > 1, то это будет означать, что среда прозрачна для излучения в j-й серии. Допустим, что мы получили β3k > 1, но β2k < 1 . Это значит, что среда непрозрачна для излучения в бальмеровской серии, но прозрачна для излучения в последующих сериях. Вспоминая соотношение (8), мы находим, что в этом случае должно быть
|
|
(28) |
или
|
|
(29) |
Вычисляя для примера отношения ![]() и
и ![]() по формулам (26) и (27) при T=20000o, получаем, что при x=1,0 должно быть
по формулам (26) и (27) при T=20000o, получаем, что при x=1,0 должно быть
|
|
(30) |
a при x=10
|
|
(31) |
Таковы условия, которые должны выполняться, если среда непрозрачна для излучения в лаймановской и бальмеровской сериях и прозрачна для излучения в других сериях. Представляет интерес нахождение бальмеровского декремента для только что рассмотренного случая. При выполнении последних условий мы должны положить βjk=1 (j=3, 4, 5,...). Тогда система уравнений (9) приводится к виду:
![\begin{eqnarray}
\left.
\begin{array}{l} n_1B_{1c}W\rho_{1c}^* = \beta_{12}\sum\limits_{k=2}^{\infty} n_k D_{1k} + n_e n^+ C_1 \nonumber \\ \\ n_2(A_{21}\beta_{12} + B_{2c}W\rho_{2c}^*) = \frac{n_1}{n_2} \beta_{12}\sum\limits_{k=3}^{\infty} n_k D_{2k} + n_e n^+ C_2 \nonumber \\ \\ n_i\left[ \beta_{12}\left( D_{1i} + \frac{n_1}{n_2} D_{2i}\right) + \sum\limits_{k=3}^{i-1} A_{ik}+B_{ic}W\rho_{ic}^* \right]= \nonumber \\ \\
= \sum\limits_{k=i+1}^{\infty} n_k A_{ki} + n_e n^+ C_i \quad (i=3,4,5,...)\nonumber
\end{array}
\right\}
\end{eqnarray}](https://images.astronet.ru/pubd/2011/06/28/0001252608/tex/formula186.gif)
|
(32) |
Система уравнений (32) была решена нами численно для следующих двух случаев:
- T=20000o, β12=10-3, W=10-3, x=1.0,
- T=20000o, β12=10-5, W=10-6, x=10.
Бальмеровский декремент, полученный в результате решения, приведен в табл. VII.
Таблица VII
Бальмеровский декремент при βjk=1 (j=3,4,5,..)
| I | II | |
| Hα | 2.0 | 8.9 |
| Hβ | 1.00 | 1.00 |
| Hγ | 0.80 | 0.91 |
| Hδ | 0.61 | 0.84 |
Из таблицы видно, что интенсивности линий Hβ, Hγ и Hδ близки друг к другу, но отношение интенсивностей ![]() весьма велико. Этот бальмеровский декремент резко отличается от полученного ранее (cм. таблицы IV и V). На самом деле из-за неоднородности оболочек возможны комбинации обоих бальмеровских декрементов.
весьма велико. Этот бальмеровский декремент резко отличается от полученного ранее (cм. таблицы IV и V). На самом деле из-за неоднородности оболочек возможны комбинации обоих бальмеровских декрементов.
В следующем параграфе мы увидим, что бальмеровский декремент указанного в табл. VII типа действительно осуществляется в некоторых оболочках.
<< 1.3 Относительные интенсивности линий | Оглавление | 1.5 Сравнение с наблюдениями >>
|
Публикации с ключевыми словами:
оболочки звезд - перенос излучения
Публикации со словами: оболочки звезд - перенос излучения | |
|
См. также:
| |