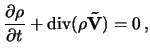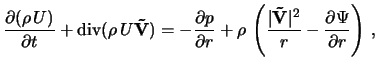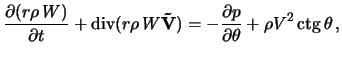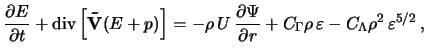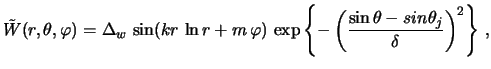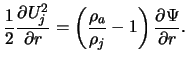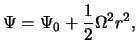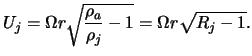Регулярные структуры в конусах ионизации в окрестности активных ядер галактик
<< 2. Равновесная модель | Оглавление | 4. Результаты нелинейного моделирования >>
3. Методика численного нелинейного моделирования
Используемая в данной части работы стационарная модель полностью аналогична описанной выше. Исключения составляют конкретные числовые значения параметров, приведенные нами в конце данного раздела.
i) основные уравнения
При численном моделировании динамики возмущений
использовалась следующая система уравнений гидродинамики в дивергентной форме
в сферической системе координат (
![]() ):
):
где
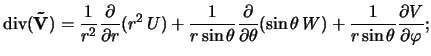
 - полная энергия;
- полная энергия;
ii) численная схема и граничные условия
Для численного интегрирования системы уравнений (14)-(18) была реализована
схема TVD-E [16], модифицированная нами для сферической системы координат,
с неравномерным шагом в радиальном направлении. Для исследования динамики
осесимметричных возмущений использовалась двумерная схема (![]() ) "2D" с
областью интегрирования (
) "2D" с
областью интегрирования (
![]() ;
;
![]() ),
содержащей
),
содержащей
![]() ячеек. Для изучения динамики
неосесимметричных возмущений использовалась трехмерная схема (
ячеек. Для изучения динамики
неосесимметричных возмущений использовалась трехмерная схема (
![]() ) "3D" с областью интегрирования (
) "3D" с областью интегрирования (
![]() ;
;
![]() ;
;
![]() ), содержащей
), содержащей
![]() ячеек.
ячеек.
Из проведенного нами линейного анализа следует, что длина
волны возмущений увеличивается линейно с радиусом, т. е.
![]() .
В соответствии с этим в численном моделировании задавался неравномерный шаг
по радиальной координате
.
В соответствии с этим в численном моделировании задавался неравномерный шаг
по радиальной координате
![]() , где
, где
![]() . При таком определении
. При таком определении ![]() количество ячеек, приходящееся на длину волны, остается постоянным вдоль
радиуса. В
количество ячеек, приходящееся на длину волны, остается постоянным вдоль
радиуса. В ![]() - и
- и ![]() -направлениях шаг интегрирования задавался
постоянным, т.е.
-направлениях шаг интегрирования задавался
постоянным, т.е.
![]() ,
,
![]() .
.
Чтобы избежать искажений в плоскости (![]() ), обусловленных
различной схемной скоростью распространения возмущений в
), обусловленных
различной схемной скоростью распространения возмущений в ![]() - и
- и ![]() -направлениях,
необходимо задавать одинаковую длину ячеек
-направлениях,
необходимо задавать одинаковую длину ячеек
![]() и
и
![]() в этих направлениях соответственно, т. е.
в этих направлениях соответственно, т. е.
![]() или
или
![]() .
.
Необходимым условием раскачки неустойчивых мод при численном
моделировании является наличие переходного слоя конечной толщины
между веществом струи и окружающей средой. Переходный слой нами
задавался размером в одну ячейку в ![]() -направлении; при таком
определении толщина переходного слоя уменьшается с увеличением
-направлении; при таком
определении толщина переходного слоя уменьшается с увеличением
![]() . Равновесные распределения в переходном слое имеют
следующий вид:
. Равновесные распределения в переходном слое имеют
следующий вид:
![]() ,
,
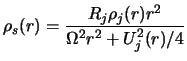 ,
,
![]() , где индексами
j, a и s обозначены величины, относящиеся к струе, окружающей
ее среде и переходному слою между ними соответственно.
, где индексами
j, a и s обозначены величины, относящиеся к струе, окружающей
ее среде и переходному слою между ними соответственно.
Начальное возмущение ![]() -компоненты скорости задавалось в следующем виде:
-компоненты скорости задавалось в следующем виде:
где
Использовались следующие граничные условия:
![]() в плоскости симметрии системы (
в плоскости симметрии системы (
![]() ) -
симметричные граничные условия
) -
симметричные граничные условия
![]() для
для ![]() ,
, ![]() ,
, ![]() ,
,
![]() и антисимметричные
и антисимметричные
![]() для
для ![]() ;
;
![]() на оси симметрии системы (
на оси симметрии системы (
![]() ) -
2D схема: симметричные граничные условия
) -
2D схема: симметричные граничные условия
![]() для
для ![]() ,
, ![]() ,
, ![]() и антисимметричные
и антисимметричные
![]() для
для ![]() ; 3D схема:
; 3D схема:
![]() ;
;
![]() при
при
![]() и
и
![]() -
периодические условия
-
периодические условия
![]() ,
,
![]() ;
;
![]() на внутренней (
на внутренней (
![]() ) и на внешней (
) и на внешней (
![]() ) по радиусу границах -
) по радиусу границах -
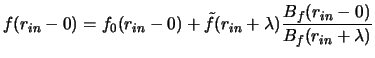 ,
,
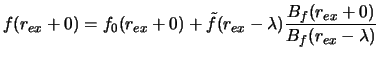 , где
, где ![]() - амплитудная функция
(огибающая возмущений),
- амплитудная функция
(огибающая возмущений), ![]() - длина волны возмущений,
индексом "0" помечены равновесные значения. В начальный момент
времени в соответствии с результатами линейного анализа
амплитудная функция определяется следующим образом:
- длина волны возмущений,
индексом "0" помечены равновесные значения. В начальный момент
времени в соответствии с результатами линейного анализа
амплитудная функция определяется следующим образом:
![]() . В последующие моменты времени
. В последующие моменты времени ![]() вычисляется
посредством аппроксимации минимумов и максимумов возмущений в
расчетных ячейках.
вычисляется
посредством аппроксимации минимумов и максимумов возмущений в
расчетных ячейках.
iii) значения параметров и способ обезразмеривания
Характеризующий итенсивность высвечивания безразмерный параметр ![]() определяется отношением двух характерных времен задачи: динамического времени
определяется отношением двух характерных времен задачи: динамического времени
![]() (времени распространения возмущений от
границ до оси симметрии струи) и времени, за которое из-за охлаждения
высвечиванием энергия газа уменьшается в
(времени распространения возмущений от
границ до оси симметрии струи) и времени, за которое из-за охлаждения
высвечиванием энергия газа уменьшается в ![]() раз:
раз:
![]() . При
. При
![]() влияние
высвечивания на динамику возмущений пренебрежимо мало. Для
значений параметра
влияние
высвечивания на динамику возмущений пренебрежимо мало. Для
значений параметра
![]() высвечивание играет важную роль в эволюции
неустойчивых мод.
высвечивание играет важную роль в эволюции
неустойчивых мод.
Расчеты проводились для
![]() ,
, ![]() либо
либо ![]() ,
углов полураствора струи
,
углов полураствора струи
![]() , либо
, либо
![]() при перепаде плотности от окружающей среды к струе
при перепаде плотности от окружающей среды к струе ![]() , либо
, либо
![]() ; в соответствии
со сказанным выше число Маха выброса составляло
; в соответствии
со сказанным выше число Маха выброса составляло
![]() либо
либо
![]() .
Для начальных возмущений задавалось
.
Для начальных возмущений задавалось ![]() ,
,
![]() либо
либо
![]() (поскольку качественных различий в результатах обеих
серий не возникло, далее описывается эксперимент с
(поскольку качественных различий в результатах обеих
серий не возникло, далее описывается эксперимент с
![]() ).
).
Необходимость задания такого сравнительно большого значения угла
раствора струи диктовалась ограниченными возможностями используемых нами
компьютеров - для корректной обработки возмущений на полураствор струи
должно приходиться хотя бы 10 ячеек расчетной области, а существенно
увеличивать ![]() мы не могли из-за недостатка оперативной памяти и
низкого быстродействия компьютеров.
мы не могли из-за недостатка оперативной памяти и
низкого быстродействия компьютеров.
Безразмерные границы расчетной области определялись значениями радиусов
![]() и
и
![]() . Согласно
сказанному выше, наше рассмотрение проводится для радиусов, отвечающих участку
твердотельного вращения диска галактики с угловой скоростью
. Согласно
сказанному выше, наше рассмотрение проводится для радиусов, отвечающих участку
твердотельного вращения диска галактики с угловой скоростью
![]() км с
км с![]() кпк
кпк
![]() (что соответствует
области внутри балджа);
размерное значение внешней границы составляет
(что соответствует
области внутри балджа);
размерное значение внешней границы составляет
![]() кпк и, следовательно, внутренней - в
кпк и, следовательно, внутренней - в ![]() раз меньше:
раз меньше:
![]() пк, в зависимости от
особенностей кривых вращения реальных галактик.
пк, в зависимости от
особенностей кривых вращения реальных галактик.
Для выбора способа обезразмеривания скорости замечаем, что из баланса давлений в струе и в окружающей ее среде следует, что уравнение (5) можно переписать в виде
Учитывая далее, что
из (20) находим:
Таким образом, естественно обезразмеривать скорость на
![]() .
Скорости звука в струе и в окружающей среде при этом однозначно определяются
безразмерными параметрами
.
Скорости звука в струе и в окружающей среде при этом однозначно определяются
безразмерными параметрами ![]() и
и ![]() . Поскольку для типичных галактик
выполняется
. Поскольку для типичных галактик
выполняется
![]() км/с, из (22) следует, что
струя должна быть высокоскоростная (для выбранного выше значения
км/с, из (22) следует, что
струя должна быть высокоскоростная (для выбранного выше значения ![]() ,
например
,
например
![]() ), несмотря на дозвуковой характер течения в ней
(
), несмотря на дозвуковой характер течения в ней
(![]() ). Это соответствует сделанному выводу о
необходимости сильного разогрева вещества струи излучением ядра галактики.
). Это соответствует сделанному выводу о
необходимости сильного разогрева вещества струи излучением ядра галактики.
Безразмерное время определялось следующим образом:
![]() . Поскольку для рассматриваемых галактик
. Поскольку для рассматриваемых галактик
![]() , то размерное значение времени
составляет
, то размерное значение времени
составляет
![]()
![]() лет.
лет.
Для обезразмеривания плотности нами было выбрано значение
![]() г/cм
г/cм![]() , что соответствует
концентрациям
, что соответствует
концентрациям
![]() см
см![]() .
.
<< 2. Равновесная модель | Оглавление | 4. Результаты нелинейного моделирования >>
|
Публикации с ключевыми словами:
Ядра галактик - джет - Сейфертовская галактика
Публикации со словами: Ядра галактик - джет - Сейфертовская галактика | |
См. также:
Все публикации на ту же тему >> | |