Астронет > Еще раз о радуге

по текстам по ключевым словам в глоссарии по сайтам перевод по каталогу

Еще раз о радуге

Е. Д. Трифонов (Российский государственный педагогический университет им. А.И. Герцена, Санкт-Петербург)
Опубликовано в Соросовском образовательном журнале, N 7, 2000 г. Содержание

Как нарисовать радугу

Теперь мы можем нарисовать схему наблюдения радуги. Такое построение выполнено на рис. 5. Сначала рисуем поверхность Земли и стоящего на ней наблюдателя. Перед наблюдателем находится завеса дождя (закрашенная серым цветом). Затем изображаем солнечные лучи, направление которых зависит от высоты Солнца над горизонтом. Через глаз наблюдателя проводим красные и фиолетовые лучи под указанными выше углами по отношению к солнечным лучам. Можно быть уверенным на основании результатов предыдущего раздела, что эти лучи возникнут в результате рассеяния на соответствующих каплях дождя. При этом, как следует из рис. 2, нижняя радуга обусловлена процессами рассеяния с одним отражением, а верхняя - с двумя отражениями. Обратите внимание на чередование цветов: фиолетовые лучи являются внешними, а красные - внутренними. Очевидно, что лучи других цветов в каждой радуге размещаются между красным и фиолетовым в соответствии со значениями показателей преломления.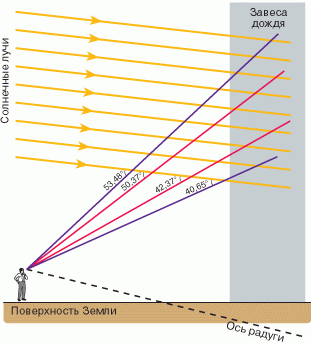

Рис. 5.Схема наблюдения радуги

Напомним, что мы пока рассматривали изображение радуги в вертикальной плоскости, проходящей через глаз наблюдателя и положение Солнца. Проведем прямую, проходящую через глаз наблюдателя параллельно солнечному лучу. Если вертикальную плоскость поворачивать вокруг указанной прямой, то ее новое положение для наблюдения радуги будет совершенно эквивалентно исходному. Поэтому радуга имеет форму дуги окружности, центр которой находится на построенной оси. Радиус этой окружности (как видно на рис. 5) приблизительно равен расстоянию наблюдателя до завесы дождя.

Отметим, что при наблюдении радуги Солнце не должно стоять слишком высоко над горизонтом - не более чем на ${53,48}^\circ$ . Иначе картина лучей на рисунке будет поворачиваться по часовой стрелке, так что даже фиолетовый луч верхней радуги не сможет попасть в глаз наблюдателя, стоящего на Земле. Правда, это окажется возможным, если наблюдатель поднимется на некоторую высоту, например на самолете. Если наблюдатель поднимется достаточно высоко, то он сможет увидеть радугу и в форме полной окружности.

Данное описание радуги следует уточнить c учетом того, что солнечные лучи не строго параллельны. Это связано с тем, что лучи, падающие на каплю от разных точек Солнца, имеют несколько различные направления. Максимальное угловое расхождение лучей определяется угловым диаметром Солнца, как известно равным приблизительно ${0,5}^\circ$ . К чему это приводит? Каждая капля испускает в глаз наблюдателя не столь монохроматический свет, как это было бы в случае строгой параллельности падающих лучей. Если бы угловой диаметр Солнца заметно превосходил угловое расстояние между фиолетовым и красным лучами, то цвета радуги были бы неразличимы. К счастью, это не так, хотя, несомненно, перекрывание лучей с разными длинами волн влияет на контрастность цветов радуги. Интересно, что конечность углового диаметра Солнца была уже учтена в работе Декарта.

Поправка на дифракцию

Приведенное выше объяснение радуги было выполнено на основании геометрической оптики. Но известно, что свет имеет волновую природу и геометрическая оптика является лишь некоторым приближением. В этом разделе мы рассмотрим, насколько это приближение оправданно в нашем случае.

Дело в том, что понятие о бесконечно узком пучке лучей является абстракцией. Если свет падает на круглое отверстие диаметра a, то из-за волновой природы (вспомните принцип Гюйгенса-Френеля) прошедший пучок света будет расширяться и угловой размер его может быть охарактеризован так называемым дифракционным углом $\lambda/a$ рад, где $\lambda$ - длина волны рассматриваемого излучения. В нашем случае свет отражается от капли. Поэтому оценка дифракционного уширения, если принять диаметр капли равным 1 мм, а длину волны 5*10^-5 см, будет 5*10^-4 рад, или ${0,03}^\circ$ .

Эту оценку легко было получить, но она является грубой. Из предыдущего объяснения радуги следует, что активными областями поверхности капли являются лишь те участки (меньшего размера), которые соответствуют экстремальным (минимальным или максимальным) значениям угла рассеяния $\varphi$ . Поэтому полученное выше дифракционное уширение является несколько заниженным. Выполним более точную оценку дифракционного уширения. Для этого аппроксимируем (то есть приближенно заменим) кривую $\varphi(y)$ в окрестности экстремальной точки параболой:

$\varphi(y) \approx \varphi_{0} + f_{0}\cdot{(y - y_{0})}^{2}$ ,

(7)

где $\varphi_{0}$ - экстремальное значение угла рассеяния, y₀ - значение прицельного расстояния, при котором достигается экстремальное значение угла $\varphi$ , f - подгоночный параметр. Из (7) следует, что

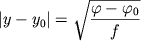$|y - y_{0}| = \sqrt{\displaystyle{\frac{\varphi - \varphi_{0}}{f}}}$ .

(8)

Заметим, что интервал | y - y₀ | характеризует интенсивность падающего на него света и равен интервалу значений прицельного параметра, из которого выходит свет (обратите внимание на симметрию хода лучей на рис. 2), поэтому он определяет и дифракционный угол. Определим интервал угла рассеяния $\varphi - \varphi_{0}$ , соответствующий интервалу прицельного параметра y - y₀ , так, чтобы он был равен дифракционному углу. То есть поставим условие

$\displaystyle{\frac{\lambda}{2R_{0}|y - y_{0}|}} = |\varphi - \varphi_{0}| = \Delta\varphi$ ,

где R₀ - радиус капли (напомним, что прицельный параметр y мы выражали в единицах радиуса капли).

Используя (8), получаем

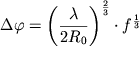$\Delta\varphi = {{\left(\displaystyle{\frac{\lambda}{2R_{0}}}\right)}^{\frac{2}{3}}}\cdot {f}^{\frac{1}{3}}$ .

(9)

Параметр f, как мы уже отмечали, может быть приближенно определен по графикам на рис. 3. Те, кто знает дифференцирование, могут выразить его, как это следует из (7), в виде

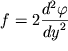
$f = 2\displaystyle{\frac{{d}^{2}\varphi}{{dy}^{2}}}$

в точке экстремума. При этом, конечно, надо дифференцировать не функцию, стоящую в правой части уравнения (7), а общие выражения для угла $\varphi$ , даваемые исходными формулами (1) и (2). Вычисления приводят к следующим результатам: f = - 4,126 в первом случае и f = 24,313 во втором. Используя эти данные, можно по формуле (9) вычислить дифракционные уширения пучков лучей в зависимости от радиуса капли. В таблице 1 мы приводим результаты этих вычислений для красного луча ( $\lambda = 7*{10}^{-7}$ м) в обеих радугах.

Таблица 1

R, мм	$\Delta\varphi_{1}$		$\Delta\varphi_{2}$
R, мм	радианы	градусы	радианы	градусы
0,1	0,0370	2,11	0,0668	3,82
0,2	0,0232	1,33	0,0421	2,41
0,5	0,0126	0,72	0,0228	1,31
1,0	0,0079	0,45	0,0144	0,82

Видно, что при радиусе капли в 1 мм дифракционное уширение порядка половины градуса для первой радуги и около одного градуса для другой. Напомним, что угловая ширина первой радуги ${1,72}^\circ$ , а второй ${3,11}^\circ$ . С уменьшением радиуса капли происходит дифракционное уширение пучков лучей разных цветов и их перекрывание. Красный цвет радуги уже плохо различим при радиусе капли в 0,1 мм. Когда радиус капли достигает значения 0,02 мм, то все цвета полностью перекрываются и радуга становится белой.

Отступая немного в сторону от нашей основной темы - радуги, мы хотели бы сформулировать (вытекающее из предыдущего) следующее общее положение: если на сферическое однородное тело падает пучок монохроматического света, то наиболее яркая часть рассеянного света сосредоточена в коническом слое, толщина которого ограничена лишь дифракционными поправками. Попробуйте посчитать сами, какая будет угловая толщина такого слоя, если диаметр шара, наполненного водой, равен 1 м.

Рецензент статьи В.В. Михайлин

Назад | Вперед

Публикации с ключевыми словами: радуга - оптика - преломление света - дисперсия света
Публикации со словами: радуга - оптика - преломление света - дисперсия света

См. также:

Радужное дерево

Полная круговая радуга над Норвегией

Дополнительные радуги над Нью-Джерси

Когда радуги улыбаются

Красная облачная радуга над Делавэром

Закат, похожий на слоеный пирог

Радуга и лучи над Брайс-Каньон

Все публикации на ту же тему >>

Мнения читателей [3]

Версия для печати

Астрометрия - Астрономические инструменты - Астрономическое образование - Астрофизика - История астрономии - Космонавтика, исследование космоса - Любительская астрономия - Планеты и Солнечная система - Солнце