Астронет > Еще раз о радуге

по текстам по ключевым словам в глоссарии по сайтам перевод по каталогу

Еще раз о радуге

Е. Д. Трифонов (Российский государственный педагогический университет им. А.И. Герцена, Санкт-Петербург)
Опубликовано в Соросовском образовательном журнале, N 7, 2000 г. Содержание

Как средь прозрачных облачных пелен
Над луком лук соцветный и сокружный
Посланницей Юноны вознесен,
И образован внутренним наружный.
Данте

Радуга у всех на виду - она обычно наблюдается в виде двух окрашенных дуг (двух соцветных луков, о которых пишет Данте), причем в верхней дуге цвета располагаются в таком порядке сверху вниз: фиолетовый, синий, зеленый, желтый, красный, а в нижней дуге наоборот - от красного до фиолетового. Наверное, не все помнят объяснение этого явления как результат преломления и отражения солнечного луча в капле дождя. А большинство из тех, кто это помнит, не смогут активно провести достаточно элементарные вычисления для ее описания. Радуге посвящено много популярных изданий, например книга М. Миннарта [Миннарт М., 1969] и книга Л.В. Тарасова [Тарасов Л.В., 1988]. В то же время в школьных учебниках и учебниках по общей физике этому явлению почти не уделяется внимания, хотя объяснения радуги занимают важное место в развитии геометрической и волновой оптики.

История объяснения радуги

Общая физическая картина радуги была уже четко описана Марком Антонием де Доминисом (1611). На основании опытных наблюдений он пришел к заключению, что радуга получается в результате отражения от внутренней поверхности капли дождя и двукратного преломления - при входе в каплю и при выходе из нее. Рене Декарт дал более полное объяснение радуги в своем труде "Метеоры" в главе "О радуге" (1635) [Декарт Р., 1953]. Декарт пишет: "Во-первых, когда я принял во внимание, что радуга может появляться не только на небе, но также и в воздухе вблизи нас каждый раз, когда в нем находятся капли воды, освещенные солнцем, как это иногда можно видеть в фонтанах, мне легко было заключить, что она зависит от того, каким образом лучи света действуют на эти капли, а от них достигают нашего глаза; далее, зная, что эти капли шарообразны, и видя, что и при больших и при малых каплях радуга появляется всегда одинаковым образом, я поставил себе целью создать очень большую каплю, чтобы иметь возможность лучше ее рассмотреть. Для этого я наполнил водой большой стеклянный сосуд, вполне круглый и вполне прозрачный и пришел к следующему выводу..."

Этот вывод повторяет и уточняет результат, полученный Доминисом. В частности, Декарт обнаружил, что вторая (внешняя) радуга возникает в результате двух преломлений и двух отражений. Он также качественно объяснил появление цветов радуги, сравнивая преломление света в капле с преломлением в стеклянной призме. Рисунок 1, поясняющий ход лучей в капле, взят из упомянутой выше работы Декарта. Но главная заслуга Декарта заключалась в том, что он количественно объяснил это явление, впервые используя закон преломления света: "Я еще не знал, почему цвета появляются лишь под известными углами, пока не взял перо и не вычислил подробно хода всех лучей, которые падают на различные точки водяной капли, чтобы узнать, под какими углами они могут попасть в наш глаз после двух преломлений и одного или двух отражений. Тогда я нашел, что после одного отражения и двух преломлений гораздо больше лучей, которые могут быть видны под углом от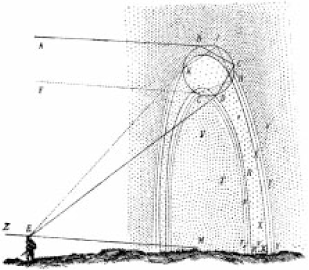 ${41}^\circ$ до ${42}^\circ$ (по отношению к солнечному лучу), чем таких, которые видны под каким-либо меньшим углом, и нет ни одного, который был бы виден под большим. Далее я нашел также, что после двух отражений и двух преломлений оказывается гораздо больше лучей, падающих в глаз под углом от ${51}^\circ$ до ${52}^\circ$ , чем таких, которые бы падали под каким-либо большим углом, и нет совсем таких, которые падали бы под меньшим".

Рис. 1.Рисунок из работы Р. Декарта, поясняющий наблюдение радуги

Таким образом Декарт не только вычисляет ход лучей, но и определяет угловое распределение интенсивности рассеянного каплями света. В следующем разделе мы покажем, как это можно сделать достаточно простыми средствами.

В отношении цветов теория радуги была дополнена Исааком Ньютоном. В известных "Лекциях по оптике" [Ньютон И., 1945], которые были написаны в 70-х годах XVI века, но опубликованы уже после смерти Ньютона в 1729 году, приведено следующее резюме: "Из лучей, входящих в шар, некоторые выходят из него после одного отражения, другие - после двух отражений; есть лучи, выходящие после трех отражений и даже большего числа отражений. Поскольку дождевые капли очень малы относительно расстояния до глаза наблюдателя, то не стоит совсем рассматривать их размеры, а только углы, образуемые падающими лучами с выходящими. Там, где эти углы наибольшие или наименьшие, выходящие лучи наиболее сгущены. Так как различные роды лучей (лучи разных цветов) составляют различные наибольшие и наименьшие углы, то лучи, наиболее плотно собирающиеся у различных мест, имеют стремление к проявлению собственных цветов".

Утверждение Ньютона о возможности не учитывать размеры капли, так же как слова Декарта о том, что при больших и малых каплях радуга появляется всегда одинаковым образом, оказалось неточным. Полная теория радуги с учетом дифракции света, которая зависит от соотношения длины волны света и размера капли, была построена лишь в XIX веке Дж.Б. Эри (1836) и Дж.М. Пернтером (1897).

Преломление и отражение луча в капле воды

Рисунок Декарта, который мы воспроизвели как реликвию, обладает одним "методическим" несовершенством. Неподготовленному читателю может показаться, что обе радуги, внешняя и внутренняя, обусловлены разными способами отражения в одной и той же капле. Лучше было бы изобразить две капли: одну, относящуюся к нижней радуге, другую к верхней, оставив в каждой по одному способу отражения, как это показано на рис. 2. Для простоты восприятия в обоих случаях направление падающего на каплю солнечного луча принято за ось абсцисс. Координату y, характеризующую точку падения луча на каплю, будем называть >прицельным параметром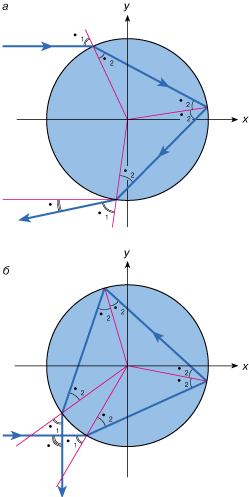

Рис. 2.Ход лучей в капле воды: а - при одном отражении, б - при двух отражениях

Из рис. 2, а видно, что падающий луч с одним отражением может быть воспринят наблюдателем, если только точка падения относится к верхней части капли (y > 0). Наоборот, при двух отражениях это окажется возможным для тех лучей, которые падают на нижнюю часть капли (y < 0).

Предположим сначала, что капля находится в вертикальной плоскости, проходящей через положение Солнца и глаз наблюдателя. Тогда падающий, преломленные и отраженные лучи лежат в этой же плоскости. Если $\alpha_{1}$ - угол падения, а $\alpha_{2}$ - угол преломления, то из рис. 2, а и б угол вышедшего луча по отношению к падающему в первом случае будет равен

$\varphi_{1} = 4\alpha_{2} - 2\alpha_{1}$ ,

(1)

а во втором -

$\varphi_{2} = \pi - 6\alpha_{2} + 2\alpha_{1}$ ,

(2)

причем, согласно закону преломления:

$\sin \alpha_{2} = \displaystyle{\frac{\sin \alpha_{1}}{n}}$

где n в нашем случае показатель преломления воды. Кроме того, принимая условно радиус капли за единицу длины, имеем

$\sin \alpha_{1} = y$ ,

$\sin \alpha_{2} = \displaystyle{\frac{y}{n}}$ ,

соответственно в первом и во втором случаях. Поэтому из (1) и (2) получаем

$\varphi_{1} = 4\arcsin \displaystyle{\frac{y}{n}} -2\arcsin y$ , y>0

(3)

$\varphi_{2} = \pi + 6\arcsin \displaystyle{\frac{y}{n}} -2\arcsin y$ , y<0

(4)

Эти два уравнения являются основными для дальнейшего рассмотрения. Нетрудно построить графики углов $\varphi_{1}$ и $\varphi_{2}$ как функций y. Они представлены на рис. 3 для показателя преломления n = 1,331 (красный цвет). Мы видим, что при значении прицельного параметра $y \approx 0,85$ достигается максимум угла $\varphi_{1}$ , приблизительно равный ${42}^\circ$ , а угол $\varphi_{2}$ имеет минимум $\sim {53}^\circ$ при $y \approx - 0,95$ . Покажем, что этим экстремальным точкам соответствует максимум интенсивности отраженного каплей света.

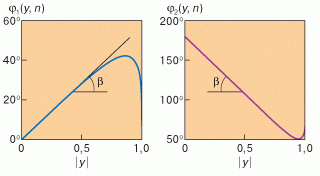Рис. 3.Зависимость угла отражения луча, падающего на каплю, от прицельного параметра

Рассмотрим некоторый малый интервал изменения прицельного параметра (для определенности в первом случае) y, y + $\Delta y$ . С помощью графика можно найти изменение угла $\varphi$ на этом интервале $\Delta\varphi$ . На рис. 3 видно, что $\Delta\varphi = \Delta y\cdot\tan \beta$ , где $\beta$ - угол, который касательная к графику в данной точке образует с осью абсцисс. Величина $\Delta y$ пропорциональна интенсивности света $\Delta I$ , падающего на каплю в этом интервале прицельного параметра. Эта же интенсивность света (точнее, пропорциональная ей величина) рассеивается каплей в угловом интервале $\Delta\varphi$ . Мы можем написать $\Delta I \sim \Delta y = \Delta\varphi\cot\beta$ . Следовательно, интенсивность рассеянного каплей света, приходящаяся на единицу угла рассеяния, может быть выражена как

$I(\varphi) = \displaystyle{\frac{\Delta I}{\Delta\varphi}} \sim \cot\beta$ .

(5)

Так как в экстремальных точках $\cot\beta = \infty$ , то величина (5) обращается в бесконечность. Отметим, что положения этих экстремальных точек для различных цветов несколько отличаются, что и позволяет наблюдать радугу. Описанный эффект получен на основании геометрической оптики. В последнем разделе мы покажем, какое влияние на него оказывает дифракция света.

Угловое распределение интенсивности рассеянного света можно получить, если построить график зависимости $\cot\beta$ от угла $varphi$ . Вручную это можно сделать по графикам на рис. 3, но лучше, конечно, на компьютере. Для тех, кто знает, что такое производная, приведенные выше рассуждения можно свести к формуле

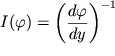$I(\varphi) = {\left( \displaystyle{\frac{d\varphi}{dy}} \right)}^{-1}$ .

(6)

Ниже мы приводим программу построения этих графиков с помощью среды Маткад (MathCad).

y:=0,0001

n:=1,331

m:=1,343

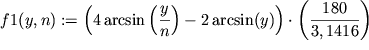
$f1(y,n):= \left(4\arcsin\left(\displaystyle{\frac{y}{n}}\right) - 2\arcsin(y)\right)\cdot\left(\displaystyle{\frac{180}{3,1416}}\right)$

$f2(y,n):= 180 - \left[\left(6\left|\arcsin\left(\displaystyle{\frac{y}{n}}\right)\right| - 2|\arcsin(y)| \right) \cdot \displaystyle{\frac{180}{3,1416}}\right]$

$df1(y,n):=\displaystyle{\frac{d}{dy}}f1(y,n)$

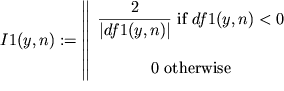
$I1(y,n):=\left\|\begin{array}{c} \displaystyle\frac{2}{|df1(y,n)|} \mbox{ if } df1(y,n)\lt0 \\\\ 0 \mbox{ otherwise} \end{array}\right.$

$df2(y,n):=\displaystyle{\frac{d}{dy}}f2(y,n)$

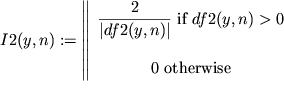
$I2(y,n):=\left\|\begin{array}{c} \displaystyle\frac{2}{|df2(y,n)|} \mbox{ if } df2(y,n)\gt0 \\\\ 0 \mbox{ otherwise} \end{array}\right.$

Эта программа очень лаконична и фактически повторяет формулы, приведенные в тексте. В первой строке задан интервал изменения модуля прицельного параметра [0, 1] с шагом 0,0001, n = 1,331 и m = 1,343 - показатели преломления воды для красного и фиолетового лучей соответственно. Далее приводятся две основные формулы для углов рассеяния (выраженные в градусах), аналогичные формулам (3) и (4). Затем записываются команды вычисления производных от этих углов по прицельному параметру и, наконец, в соответствии с (6) задаются формулы для вычисления относительных интенсивностей. Для упрощения программы мы предполагаем здесь симметрию кривых на рис. 3 в окрестности экстремальных точек. С этим связано введенное условие "if " и дополнительный множитель 2.

Полученные таким образом графики интенсивности рассеянного света для первого и второго случаев изображены на рис. 4. При этом мы показываем кривые для двух значений показателя преломления, соответствующих красному и фиолетовому цветам.

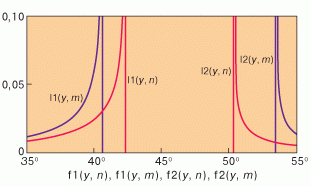Рис. 4.Угловое распределение интенсивности отраженного каплей монохроматического света, полученное с помощью геометрической оптики

Приведем значения углов, при которых достигаются максимумы интенсивностей красного и фиолетового лучей:
     фиолетовый луч в первом случае ${40,65}^\circ$ ,
     красный луч в первом случае ${42,37}^\circ$ ,
     фиолетовый луч во втором случае ${53,48}^\circ$ ,
     красный луч во втором случае ${50,37}^\circ$ .
Видно, что яркие лучи, окрашенные в эти цвета, в рассматриваемом приближении хорошо разделены: в первом случае - на ${1,72}^\circ$ , во втором - на ${3,11}^\circ$ . Таким образом, эффект радуги обусловлен тем, что под определенными углами возникают максимумы интенсивности рассеянного света и для разных цветов положения этих максимумов не перекрываются.

Назад | Вперед

Публикации с ключевыми словами: радуга - оптика - преломление света - дисперсия света
Публикации со словами: радуга - оптика - преломление света - дисперсия света

См. также:

Радужное дерево

Полная круговая радуга над Норвегией

Дополнительные радуги над Нью-Джерси

Когда радуги улыбаются

Красная облачная радуга над Делавэром

Закат, похожий на слоеный пирог

Радуга и лучи над Брайс-Каньон

Все публикации на ту же тему >>

Мнения читателей [3]

Версия для печати

Астрометрия - Астрономические инструменты - Астрономическое образование - Астрофизика - История астрономии - Космонавтика, исследование космоса - Любительская астрономия - Планеты и Солнечная система - Солнце