<< 9. Геометрия решения Шварцшильда | Оглавление | 11. Вращающиеся черные дыры >>
10. Черные дыры с электрическим зарядом
Анализ эволюции звезд привел астрономов к заключению, что как в нашей Галактике, так и вообще во Вселенной могут существовать черные дыры. В двух предыдущих главах мы рассмотрели ряд свойств самых простых черных дыр, которые описываются тем решением уравнения гравитационного поля, которое нашел Шварцшильд. Шварцшильдовская черная дыра характеризуется только массой; электрического заряда у нее нет. У нее отсутствует также магнитное поле и вращение. Все свойства шварцшильдовской черной дыры однозначно определяются заданием одной только массы той звезды, которая, умирая, превращается в черную дыру в ходе гравитационного коллапса.
Нет сомнений, что решение Шварцшильда - чересчур простой случай. Настоящая черная дыра должна по крайней мере вращаться. Однако сколь сложной может быть черная дыра на самом деле? Какие добавочные подробности следует учесть, а какими можно пренебречь при полном описании той черной дыры, которую можно обнаружить при наблюдениях неба?
Представим себе массивную звезду, у которой только что кончились все ресурсы ядерной энергии и у которой вот-вот начнется фаза катастрофического гравитационного коллапса. Можно думать, что такая звезда обладает очень сложной структурой и при ее всестороннем описании пришлось бы учитывать множество характеристик. В принципе астрофизик способен рассчитать химический состав всех слоев такой звезды, изменение температуры от ее центра до поверхности и получить все данные о состоянии вещества в недрах звезды (например, его плотности и давления) на всевозможных глубинах. Такие расчеты сложны, и их результаты существенно зависят от всей истории развития звезды. Внутреннее строение звезд, образовавшихся из разных облаков газа и в разное время, заведомо должно быть различным.
Однако, несмотря на все эти осложняющие обстоятельства, существует один бесспорный факт. Если масса умирающей звезды превышает примерно три массы Солнца, эта звезда непременно превратится в черную дыру в конце своего жизненного цикла. Не существует таких физических сил, которые могли бы предотвратить коллапс столь массивной звезды.
Чтобы лучше осознать смысл этого утверждения, вспомним, что черная дыра - это столь искривленная область пространства-времени, что из нее ничто не может вырваться, даже свет! Другими словами, из черной дыры невозможно получить никакую информацию. Как только вокруг умирающей массивной звезды возник горизонт событий, становится невозможным выяснить какие бы то ни было детали того, что происходит под этим горизонтом. Наша Вселенная навсегда теряет доступ к информации о событиях под горизонтом событий. Поэтому черную дыру иногда называют могилой для информации.
Хотя при коллапсе звезды с появлением черной дыры и теряется огромное количество информации, все же некоторая информация извне остается. Например, сильнейшее искривление пространства-времени вокруг черной дыры указывает, что здесь умерла звезда. С массой мертвой звезды прямо связаны такие конкретные свойства дыры, как поперечник фотонной сферы или горизонта событий (см. рис. 8.4 и 8.5). Хотя сама дыра в буквальном смысле черная, космонавт еще издалека обнаружит ее существование по гравитационному полю дыры. Измерив, насколько траектория его космического корабля отклонилась от прямолинейной, космонавт может точно вычислить полную массу черной дыры. Таким образом, масса черной дыры - это один из элементов информации, который не теряется при коллапсе.
Чтобы подкрепить это утверждение, рассмотрим пример двух одинаковых звезд, образующих при коллапсе черные дыры. На одну звезду поместим тонну камней, а на другую - слона весом в одну тонну. После образования черных дыр измерим напряженность гравитационного поля на больших расстояниях от них, скажем, по наблюдениям орбит их спутников или планет. Окажется, что напряженности обоих полей одинаковы. На очень больших расстояниях от черных дыр для вычисления полной массы каждой из них можно воспользоваться ньютоновской механикой и законами Кеплера. Так как полные суммы масс входящих в каждую из черных дыр составных частей одинаковы, идентичными окажутся и результаты. Но что еще существеннее, это невозможность указать, какая из этих дыр поглотила слона, а какая - камни. Вот эта информация пропала навсегда. Тонну чего бы вы ни бросили в черную дыру, результат всегда будет одним и тем же. Вы сможете определить, какую массу вещества поглотила дыра, но сведения о том, какой формы, какого цвета, какого химического состава было это вещество, утрачиваются навсегда.
Полную массу черной дыры всегда можно измерить, поскольку гравитационное поле дыры влияет на геометрию пространства и времени на огромных расстояниях от нее. Находящийся далеко от черной дыры физик может поставить эксперименты по измерению этого гравитационного поля, например запустив искусственные спутники и наблюдая их орбиты. Это важный источник информации, позволяющий физику с уверенностью говорить, что именно черная дыра не поглотила. В частности, все, что может измерить этот гипотетический исследователь вдали от черной дыры, не было поглощено полностью.
Начиная в середине XIX в. разработку теории электромагнетизма, Джеймс Клерк Максвелл располагал большими количествами информации об электрическом и магнитном полях. В частности, удивительным был тот факт, что электрические и магнитные силы убывают с расстоянием в точности так же, как и сила тяжести. И гравитационные, и электромагнитные силы - это силы большого радиуса действия. Их можно ощутить на очень большом удалении от их источников. Напротив, силы, связывающие воедино ядра атомов, - силы сильного и слабого взаимодействий - имеют короткий радиус действия. Ядерные силы дают о себе знать лишь в очень малой области, окружающей ядерные частицы.
Большой радиус действия электромагнитных сил означает, что физик, находясь далеко от черной дыры, может предпринять эксперименты для выяснения, заряжена эта дыра или нет. Если у черной дыры имеется электрический заряд (положительный или отрицательный) или магнитный заряд (соответствующий северному или юному магнитному полюсу), то находящийся вдалеке физик способен при помощи чувствительных приборов обнаружить существование этих зарядов. Таким образом, кроме информации о массе не теряется также информация о заряде черной дыры.
Существует третий (и последний) важный эффект, который может измерить удаленный физик. Как будет видно из следующей главы, любой вращающийся объект стремится вовлечь во вращение окружающее его пространство-время. Это явление называется эффектом Лензе-Тирринга или эффектом увлечения инерциальных систем. Наша Земля при вращении тоже увлекает за собой пространство и время, но в очень малой степени. Но для быстро вращающихся массивных объектов этот эффект становится заметнее, и если черная дыра образовалась из вращающейся звезды, то увлечение пространства-времени вблизи нее будет вполне ощутимым. Физик, находящийся в космическом корабле вдали от этой черной дыры, заметит, что он постепенно вовлекается во вращение вокруг дыры в ту же сторону, в которую вращается она сама. И чем ближе к вращающейся черной дыре окажется наш физик, тем сильнее будет это вовлечение.
Рассматривая любое вращающееся тело, физики часто говорят о его Моменте количества движения; это - величина, определяемая как массой тела, так и скоростью его вращения. Чем быстрее вращается тело, тем больше его момент количества движения. Помимо массы и заряда момент количества движения черной дыры является той ее характеристикой, информация о которой не теряется.
В конце 1960-х - начале 1970-х годов астрофизики-теоретики упорно трудились над проблемой: информация о каких свойствах черных дыр сохраняется, а о каких - теряется в них? Плодом их усилий оказалась знаменитая теорема о том, что "у черной дыры нет волос", впервые сформулированная Джонов Уилером из Принстонского университета (США). Мы уже виде ли, что характеристики черной дыры, которые могут быть измерены удаленным наблюдателем, - это ее масса, ее заряд и ее момент количества движения. Эти три основные характеристики сохраняются при образовании черной дыры и определяют геометрию пространства-времени вблизи нее. Работами Стивена Хоукинга, Вернера Израэля, Брандона Картера, Дэвида Робинсона и других исследователей было показано, что только эти характеристики сохраняются при образовании черных дыр. Иными словами, если задать массу, заряд и момент количества движения черной дыры, то о ней уже будет известно все - у черных дыр нет иных свойств, кроме массы, заряда и момента количества движения. Таким образом, черные дыры - это очень простые объекты; они гораздо проще, чем звезды, из которых черные дыры возникают. Для полного описания звезды требуется знание большого количества характеристик, таких, как химический состав, давление, плотность и температура на разных глубинах. Ничего подобного у черной дыры нет (рис. 10.1). Право же, у черной дыры совсем нет волос!
Поскольку черные дыры полностью описываются тремя параметрами (массой, зарядом и моментом количества движения), то должно существовать лишь несколько решений уравнений гравитационного поля Эйнштейна, причем каждое описывает свой "добропорядочный" тип черных дыр. Например, в предыдущих двух главах мы рассмотрели простейший тип черной дыры; эта дыра имеет лишь массу, и ее геометрия определяется решением Шварцшильда. Решение Шварцшильда было найдено в 1916 г., и хотя с тех пор было получено много других решений для черных дыр, обладающих только массой, все они оказались ему эквивалентными.
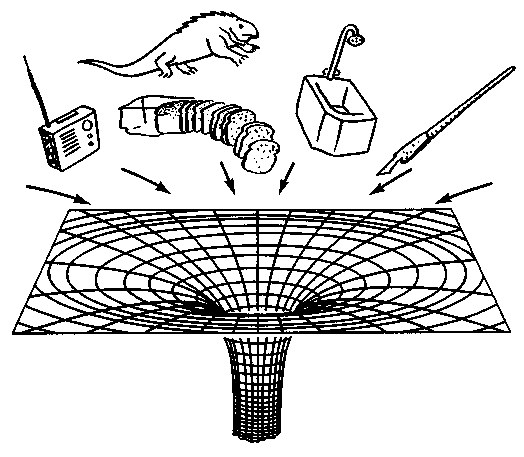
|
| Рис. 10.1. "У черной дыры нет волос!" Почти всякая информация о телах, падающих в черную дыру, теряется навсегда. Избегают "переваривания" дырой только масса, заряд и момент количества движения падающих в нее объектов. Это значит, что черные дыры - очень простые объекты. Их полное описание характеризуется всего тремя параметрами - массой, зарядом и моментом импульса. (По Дж. Уилеру.) |
Невозможно представить себе, как могли бы черные дыры образоваться без вещества. Поэтому у любой черной дыры должна быть масса. Но вдобавок к массе у дыры могли бы существовать электрический заряд или вращение или и то, и другое вместе. Между 1916 и 1918 гг. Г. Райснер и Г. Нордстрём нашли решение уравнений поля, описывающее черную дыру с массой и зарядом. Следующий шаг на этом пути задержался до 1963 г., когда Рой П. Керр нашел решение для черной дыры, обладающей массой и моментом количества движения. Наконец, в 1965 г. Ньюмэн, Коч, Чиннапаред, Экстон, Пракаш и Торренс опубликовали решение для самого сложного типа черной дыры, а именно для дыры с массой, зарядом и моментом количества движения. Каждое из этих решений единственно - других возможных решений нет. Черная дыра характеризуется, самое большее, тремя параметрами - массой (обозначаемой через M) зарядом (электрическим или магнитным, обозначается через Q) и моментом количества движения (обозначается через а). Все эти возможные решения сведены в табл. 10.1.
| Таблица 10.1 | ||||||||||||||||||||
| Решения уравнений поля, описывающие черные дыры. | ||||||||||||||||||||
|
Геометрия черной дыры решающим образом зависит от введения каждого дополнительного параметра (заряда, вращения или их вместе). Решения Райснера-Нордстрёма и Керра сильно отличаются как друг от друга, так и от решения Шварцшильда. Конечно, в пределе, когда заряд и момент количества движения обращаются в нуль (Q -> 0 и а -> 0), все три более сложных решения сводятся к решению Шварцшильда. И все же черные дыры, обладающие зарядом и/или моментом количества движения, имеют ряд замечательных свойств.
Во время первой мировой войны Г. Райснер и Г. Нордстрём открыли решение эйнштейновских уравнений гравитационного поля, полностью описывающее "заряженную" черную дыру. У такой черной дыры может быть электрический заряд (положительный или отрицательный) и/или магнитный заряд (соответствующий северному или южному магнитному полюсу). Если электрически заряженные тела - дело обычное, то магнитно заряженные - вовсе нет. Тела, у которых есть магнитное поле (например, обычный магнит, стрелка компаса, Земля), обладают обязательнољ иљ севернымљ иљ южнымиљ полюсамиљљ сразу.љљ Дољљ самого последнегољ времениљ большинствољ физиковљ считали,љ чтољљ магнитныељљ полюсыљљ всегдаљљ встречаютсяљљ толькољљ парами.љљ Однако в 1975 г. группа ученых из Беркли и Хьюстона объявила, что в ходе одного из экспериментов ими открыт магнитный монополь. Если эти результаты подтвердятся, то окажется, что могут существовать и отдельные магнитные заряды, т.е. что северный магнитный полюс может существовать отдельнољ от южного, и обратно. Решение Райснера-Нордстрёма допускает возможность существования у черной дыры магнитного поля монополя. Независимо от того, как черная дыра приобрела свой заряд, все свойства этого заряда в решении Райснера-Нордстрёма объединяются в одну характеристику - число Q. Эта особенность аналогична тому факту, что решение Шварцшильда не зависит от того, каким образом черная дыра приобрела свою массу. Ее могли составить слоны, камни или звезды - конечный результатљ будет всегда одним и тем же. При этом геометрия пространства-времени в решении Райснера-Нордстрёма не зависит от природы заряда. Он может быть положительным, отрицательным, соответствовать северномуљ магнитномуљ полюсуљ илиљ южному - важно лишь его полное значение, которое можно записать как |Q|. Итак,љљ свойстваљљ чернойљљ дырыљљ Райснера-Нордстрёмаљљ зависят лишь от двух параметров - полной массы дыры М и ее полного зарядаљ |Q|љљ (инымиљљ словами,љљ отљ егољљ абсолютнойљљ величины). Размышляя о реальных черных дырах, которые могли бы реально существовать в нашей Вселённой, физики пришли к заключению, что решение Райснера-Нордстрёма оказывается не очень существенным, ибо электромагнитные силы намного больше сил тяготения. Например, электрическое поле электрона или протона в триллионы триллионов раз сильнее их гравитационного поля. Это значит, что если у черной дыры был бы достаточно большой заряд, то огромные силы электромагнитного происхождения быстро разбросали бы во все стороны газ и атомы, "плавающие" в космосе. В самое короткое время частицы, имеющие такой же знак заряда, как и черная дыра, испытали бы мощное отталкивание, а частицы с противоположным знаком заряда - столь же мощное притяжение к ней. Притягивая частицы с зарядом противоположного знака, черная дыра вскоре стала бы электрически нейтральной. Поэтому можно полагать, что реальные черные дыры обладают зарядом лишь малой величины. Для реальных черных дыр значение |Q| должно быть гораздо меньше, чем М. В самом деле, из расчетов следует, что черные дыры, которые могли бы реально существовать в космосе, должны иметь массу М по крайней мере в миллиард миллиардов раз большую, чем величина |Q|. Математически это выражается неравенством
Несмотря на эти, увы, прискорбные ограничения, налагаемые законами физики, весьма поучительно провести подробный анализ решения Райснера-Нордстрёма. Такой анализ подготовит нас к более основательному обсуждению решения Керра в следующей главе.
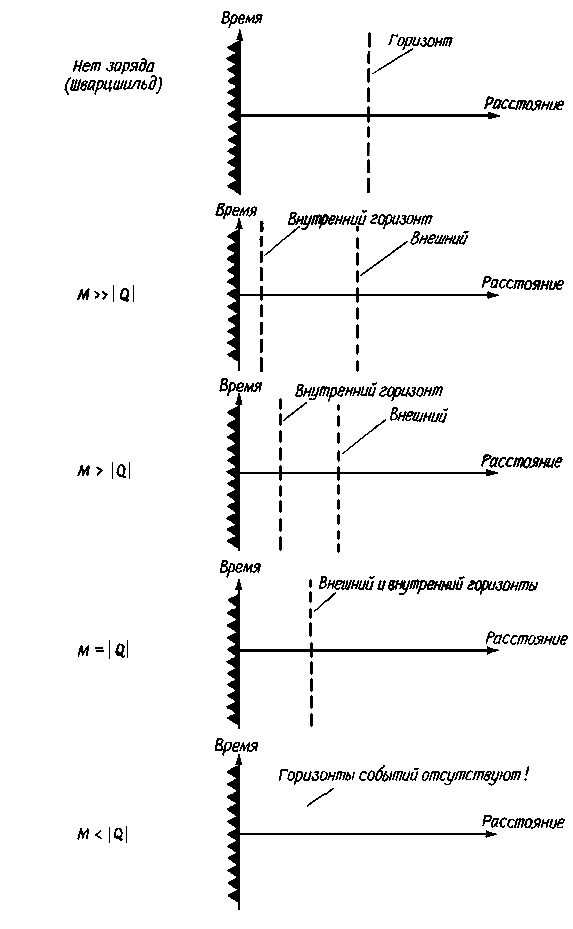
Чтобы проще подойти к пониманию особенностей решения Райснера-Нордстрёма, рассмотрим обычную черную дыру без заряда. Как следует из решения Шварцшильда, такая дыра состоит из сингулярности, окруженной горизонтом событий. Сингулярность расположена в центре дыры (при r=0), а горизонт событий - на расстоянии 1 шварцшильдовского радиуса (именно при r=2М). Теперь представим себе, что мы придали этой черной дыре небольшой электрический заряд. Как только у дыры появился заряд, мы должны обратиться к решению Райснера-Нордстрёма для геометрии пространства-времени. В решении Райснера-Нордстрёма имеются два горизонта событий. Именно, с точки зрения удаленного наблюдателя, существуют два положения на разных расстояниях от сингулярности, где время останавливает свой бег. При самом ничтожном заряде горизонт событий, находившийся ранее на "высоте" 1 шварцшильдовского радиуса, сдвигается немножко ниже к сингулярности. Но еще более удивительно то, что сразу же вблизи сингулярности возникает второй горизонт событий. Таким образом сингулярность в заряженной черной дыре окружена двумя горизонтами событий - внешним и внутренним. Структуры незаряженной (шварцшильдовской) черной дыры и заряженной черной дыры Райснера-Нордстрёма (при М>>|Q|) сопоставлены на рис. 10.2.
Если мы будем увеличивать заряд черной дыры, то внешний горизонт событий станет сжиматься, а внутренний - расширяться. Наконец, когда заряд черной дыры достигнет значения, при котором выполняется равенство М=|Q|, оба горизонта сливаются друг с другом. Если увеличить заряд еще больше, то горизонт событий полностью исчезнет, и остается "голая" сингулярность. При М<|Q| горизонты событий отсутствуют, так что сингулярность открывается прямо во внешнюю Вселенную. Такая картина нарушает знаменитое "правило космической этики", предложенное Роджером Пенроузом. Это правило ("нельзя обнажать сингулярность!") будет подробнее обсуждаться ниже. Последовательность схем на рис. 10.3 иллюстрирует расположение горизонтов событий у черных дыр, имеющих одну и ту же массу, но разные значения заряда.
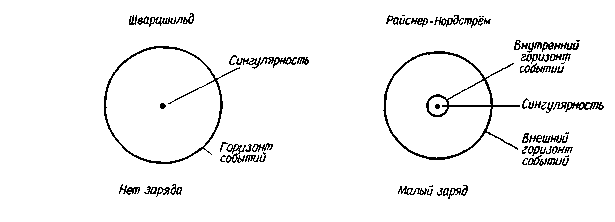
|
| Рис. 10.2. Заряженные и нейтральные черные дыры. Добавление хотя бы ничтожного по величине заряда приводит к появлению второго (внутреннего) горизонта событий прямо над сингулярностью. |

|
| Рис. 10.3. Изображение заряженных черных дыр в пространстве. По мере добавления заряда в черную дыру внешний горизонт событий постепенно сжимается, а внутренний - расширяется. Когда полный заряд дыры достигает значения |Q|= М, оба горизонта сливаются в один. При еще больших значениях заряда горизонт событий вообще исчезает и остается открытая, или "голая", сингулярность. |
Рис. 10.3 иллюстрирует положение горизонтов событий относительно сингулярности черных дыр в пространстве, но еще полезнее проанализировать диаграммы пространства-времени для заряженных черных дыр. Чтобы построить такие диаграммы - графики зависимости времени от расстояния, мы начнем с "прямолинейного" подхода, использованного в начале предыдущей главы (см. рис. 9.3). Измеряемое наружу от сингулярности расстояние откладывается по горизонтали, а время, как обычно, - по вертикали. На такой диаграмме левая часть графика всегда ограничивается сингулярностью, описываемой линией, идущей вертикально от удаленного прошлого к далекому будущему. Мировые линии горизонтов событий также представляют собой вертикали и отделяют внешнюю Вселенную от внутренних областей черной дыры.
На рис. 10.4 показаны диаграммы пространства-времени для нескольких черных дыр, имеющих одинаковые массы, но разные заряды. Вверху для сравнения приведена диаграмма для шварцшильдовской черной дыры (вспомним, что решение Шварцшильда - это то же, что решение Райснера-Нордстрёма при |Q|=0). Если этой дыре добавить совсем небольшой заряд, то второй
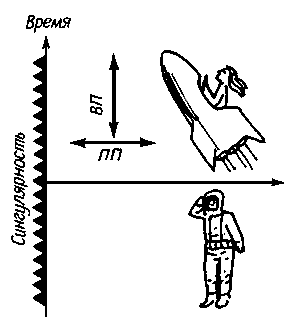
|
| Рис. 10.5. "Голая" сингулярность. Черную дыру, заряд которой чудовищно (М<|Q|), вообще не окружает горизонт событий. Вопреки "закону космической этики" сингулярность красуется на виду у всей внешней Вселенной. |
Неожиданности решения Райснера-Нордстрёма не исчерпываются двумя горизонтами событий и гравитационным отталкиванием вблизи сингулярности. Вспоминая сделанный выше подробный анализ решения Шварцшильда, можно думать, что диаграммы типа изображенных на рис. 10.4 описывают далеко не все стороны картины. Так, в геометрии Шварцшильда мы столкнулись с большими трудностями, вызванными наложением друг на друга в упрощенной диаграмме разных областей пространства-времени (см. рис. 9.9). Такие же трудности ждут нас и в диаграммах типа рис. 10.4, так что пора перейти к их выявлению и преодолению.
Легче понять глобальную структуру пространства-времени, применяя следующие элементарные правила. Выше мы разобрались, в чем состоит глобальная структура шварцшильдовской черной дыры. Соответствующая картина, именуемая диаграммой Пенроуза, изображена на рис. 9.18. Она может быть названа и диаграммой Пенроуза для частного случая черной дыры Райснера-Нордстрёма, когда заряд отсутствует (|Q|=0). Более того, если мы лишим дыру Райснера-Нордстрёма заряда (т.е. перейдем к пределу |Q|->0), то наша диаграмма (какой бы она ни была) обязательно сведется в пределе к диаграмме Пенроуза для решения Шварцшильда. Отсюда следует наше первое правило: должна существовать другая Вселенная, противоположная нашей, достижение которой возможно лишь по запрещенным пространственноподобным линиям.
При построении диаграммы Пенроуза для заряженной черной дыры появляются основания ожидать существования множества Вселенных. У каждой из них должно быть пять типов бесконечностей
Чтобы прийти к третьему правилу, напомним, что на диаграмме Пенроуза (см. рис. 9.18) горизонт событий шварцшильдовской черной дыры имел наклон 45њ. Итак, третье правило: любой горизонт событий должен быть светоподобен, и поэтому всегда имеет наклон 45њ.
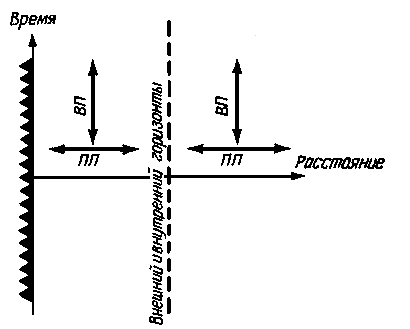
Для вывода четвертого (и последнего) правила вспомним, что при переходе через горизонт событий пространство и время менялись ролями в случае шварцшильдовской черной дыры. Из подробного анализа пространственноподобных и временноподобных направлений для заряженной черной дыры следует, что и здесь получится та же картина. Отсюда четвертое правило: пространство и время меняются ролями всякий раз, когда пересекается горизонт событий.
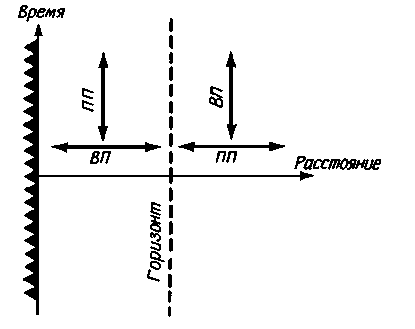
На рис. 10.7 только что сформулированное четвертое правило проиллюстрировано для случая черной дыры с малым или умеренным зарядом (М>|Q|). Вдали от такой заряженной черной дыры пространственноподобное направление параллельно пространственной оси, а временноподобное - параллельно временной оси. Пройдя под внешний горизонт событий, мы обнаружим смену ролей этих двух направлений - пространственноподобное направление теперь стало параллельно оси времени, а временноподобное - параллельно пространственной оси. Однако, продолжая Движение к центру и опустившись под внутренний горизонт событий, мы становимся свидетелями второй смены ролей. Вблизи сингулярности ориентация пространственноподобного и временнеподобного направлений становится такой же, какой она была вдали от черной дыры.

|
| Рис. 10.7. Смена ролей пространства и времени (для М>|Q|). Всякий раз при пересечении горизонта событий пространство и время меняются ролями. Это значит, что в заряженной черной дыре из-за наличия двух горизонтов событий полная смена ролей у пространства и времени происходит дважды. |
Двукратная смена ролей пространственноподобного и временноподобного направлений имеет решающее значение для природы сингулярности заряженной черной дыры. В случае шварцшильдовской черной дыры, у которой нет заряда, пространство и время меняются ролями всего один раз. Внутри единственного горизонта событий линии постоянного расстояния направлены в пространственноподобном (горизонтальном) направлении. Значит, линия, изображающая расположение сингулярности (r=0), должна быть горизонтальной, т.е. направлена пространственноподобно. Однако, когда имеются два горизонта событий, линии постоянного расстояния вблизи сингулярности имеют временноподобное (вертикальное) направление. Поэтому линия, описывающая положение сингулярности заряженной дыры (r=0), должна быть вертикальной, и ее следует ориентировать временноподобно. Поэтому так мы приходим к заключению первостепенной важности: сингулярность заряженной черной дыры должна быть временноподобной!
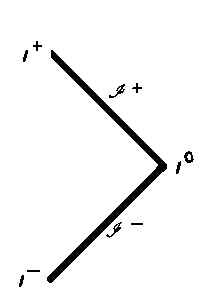
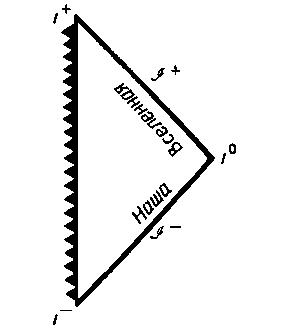
Теперь можно, воспользовавшись приведенными выше правилами, построить диаграмму Пенроуза для решения Райснера-Нордстрёма. Начнем с того, что представим себе космонавта, находящегося в нашей Вселенной (скажем, просто на Земле). Он садится в свой космический корабль, включает двигатели и направляется к заряженной черной дыре. Как видно из рис. 10.8, наша Вселенная имеет на диаграмме Пенроуза вид треугольника с пятью бесконечностями. Любой допустимый путь космонавта должен быть ориентирован на диаграмме всегда под углом менее 45њ к вертикали, так как лететь со сверхсветовой скоростью он не может.
Следует подчеркнуть, что при построении этих диаграмм Пенроуза мы снова встречаемся как с черными, так и с белыми дырами. Космонавт может выскочить наружу сквозь горизонты событий и оказаться во внешней Вселенной будущего. Большинство физиков убеждены, что белых дыр в природе в принципе быть не может. Но мы все же продолжим теоретический разбор глобальной структуры пространства-времени, включающей существование бок о бок друг с другом черных и белых дыр. Доводы же, свидетельствующие против существования белых дыр, мы отложим до гл. 14.
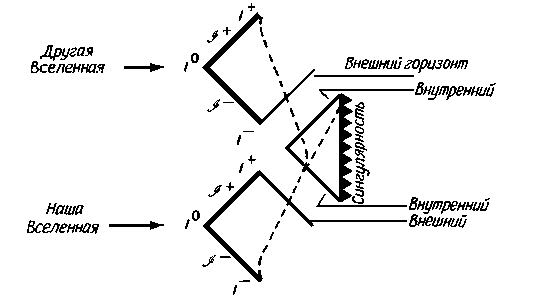
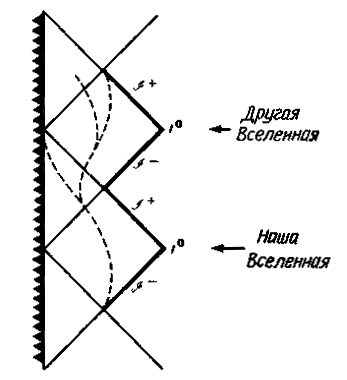
Изложенные эпизоды полета и диаграммы на рис. 10.8 должны быть не более чем фрагментом некоего целого. Диаграмму Пенроуза для заряженной черной дыры необходимо дополнить по крайней мере одним экземпляром другой Вселенной, противоположной нашей, которая достижима лишь по (запрещенным) пространственноподобным мировым линиям. Такой вывод основывается на нашем правиле 1: если удалить из черной дыры ее заряд, то диаграмма Пенроуза должна свестись к изображению решения Шварцшильда. И хотя никто из нашей Вселенной никогда не сможет проникнуть в эту "другую" Вселенную ввиду невозможности двигаться быстрее света, мы все же можем себе представить космонавта из той, другой Вселенной, путешествующего к той же самой заряженной черной дыре. Его возможные мировые линии изображены на рис. 10.9.
Такое путешествие чужого космонавта из другой Вселенной выглядит совершенно так же, как путешествие космонавта, вылетевшего из нашей Вселенной, с Земли. Чужая Вселенная также изображается на диаграмме Пенроуза привычным треугольником. По пути к заряженной черной дыре чужой космонавт пересекает внешний горизонт событий, который должен иметь наклон 45њ. Позднее он опускается и под внутренний горизонт событий, также с наклоном 45њ. Чужак стоит теперь перед выбором: либо разбиться о временноподобную сингулярность (она вертикальна на диаграмме Пенроуза), либо свернуть и снова пересечь внутренний горизонт событий. Чтобы избежать прискорбного конца, чужак решает покинуть черную дыру и выходит через внутренний горизонт событий, который, как обычно, имеет наклон 45њ. Затем он пролетает и через внешний горизонт событий (наклоненный на диаграмме Пенроуза на 45њ) в новую Вселенную будущего.
Каждое из этих двух гипотетических путешествий охватывает только две части полной диаграммы Пенроуза. Полная же картина получается, если просто объединить эти части друг с другом, как показано на рис. 10.10.
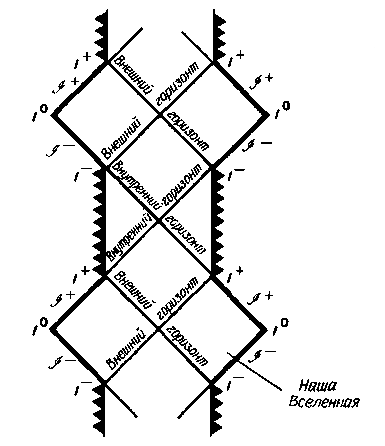
|
| Рис. 10.10. Полная диаграмма Пенроуза для черной дыры Райснера-Нордстрёма (М > > |Q|). Полную диаграмму Пенроуза для черной дыры, имеющей малый или умеренный заряд (М > |Q|), можно построить, соединяя участки, изображенные на рис. 10.8 и 10.9. Эта диаграмма повторяется до бесконечности как в будущее, так и в прошлое. |
Только что описанный подход к выяснению глобальной структуры пространства-времени касался случая черных дыр с малым или небольшим зарядом (М>|Q|). Однако в случае предельной черной дыры Райснера-Нордстрёма (когда М=|Q|) заряд оказывается настолько большим, что внутренний и внешний горизонты сливаются друг с другом. Такое объединение двух горизонтов событий приводит к ряду интересных последствий.
Вспомним, что вдали от заряженной черной дыры (вне внешнего горизонта событий) пространственноподобное направление параллельно пространственной оси, а временноподобное параллельно оси времени. Вспомним также, что вблизи сингулярности (под внутренним горизонтом событий - после того, как пространство и время дважды поменяются ролями) пространственноподобное направление снова параллельно пространственной оси, а временноподобное - оси времени. По мере того как заряд черной дыры Райснера-Нордстрема все больше и больше увеличивается, область между двумя горизонтами событий все уменьшается и уменьшается. Когда же, наконец, заряд возрастает настолько, что М=|Q|, эта промежуточная область сожмется до нуля. Следовательно, при переходе через объединенный внешне - внутренний горизонт событий пространство и время не меняются ролями. Конечно, можно с тем же успехом говорить и о двукратной смене ролей у пространства и времени, происходящей одновременно на единственном горизонте событий предельной черной дыры Райснера-Нордстрёма. Как показано на рис. 10.11, временноподобное направление в ней повсюду параллельно оси времени, а пространственноподобное - везде параллельно пространственной оси.
Хотя у предельной черной дыры Райснера-Нордстрёма имеется только один горизонт событий, положение здесь совсем иное, чем в случае шварцшильдовской черной дыры, у которой горизонт событий тоже всего один. При одиночном горизонте событий всегда имеет место смена ролей пространственно- и временноподобных направлений, как это видно на рис. 10.12. Однако у предельной черной дыры Райснера-Нордстрёма горизонт событий можно трактовать как "двойной", т.е. как наложенные друг на друга внутренний и внешний горизонты. Именно поэтому смены ролей пространства и времени не происходит.
|
| Рис. 10.12. Диаграмма пространства-времени для шварцшильдовской черной дыры (|Q|=0). Хотя у шварцшильдовской черной дыры (не имеющей заряда) есть лишь один горизонт событий, при переходе с одной его стороны на другую пространство и время меняются ролями. (Ср. с рис. 10.11.) |
Факт слияния внешнего и внутреннего горизонтов событий у предельной черной дыры Райснера-Нордстрёма означает, что требуется новая диаграмма Пенроуза. Как и прежде, ее можно построить, рассматривая мировую линию гипотетического космонавта. При этом список правил остается прежним, за тем существенным исключением, что при пересечении горизонта событий пространство и время не меняются ролями.
|
| Рис. 10.13. Диаграмма Пенроуза для предельной черной дыры Райснера-Нордстрёма (М=|Q|). Диаграмму глобальной структуры пространства-времени можно построить, если рассмотреть возможные мировые линии космонавта, ныряющего в предельную черную дыру Райснера-Нордстрёма и выныривающего из нее. |
С точки зрения математики допустима и черная дыра с огромным зарядом М<|Q|; правда, она не имеет смысла с точки зрения физики. В этом случае горизонты событий попросту исчезают, остается лишь "голая" сингулярность. Ввиду отсутствия горизонтов событий не может быть и речи о каком-то обмене ролями между пространством и временем. Сингулярность просто находится у всех на виду. "Голая" сингулярность - это не закрытая никакими горизонтами область бесконечно сильно искривленного пространства-времени.
|
| Рис. 10.14. "Голая" сингулярность. У "голой" сингулярности (М<|Q|) горизонтов событий нет. Черная дыра этого типа не связывает нашу Вселенную с какой-либо другой Вселенной. |
Поскольку у реальных черных дыр могут быть лишь очень слабые заряды (если они есть у них вообще), то значительная часть описанного выше представляет лишь академический интерес. Однако мы в результате установили безотказно действующие правила построения сложных диаграмм Пенроуза. Хотя заряженные черные дыры, видимо, не играют роли в астрофизике, вращающиеся черные дыры для нее очень важны. Астрофизики даже предполагают, что реальные черные дыры могут вращаться с гигантскими скоростями, а те методы, которые были развиты выше, окажутся весьма полезными для анализа керровских черных дыр.
<< 9. Геометрия решения Шварцшильда | Оглавление | 11. Вращающиеся черные дыры >>
|
Публикации с ключевыми словами:
черные дыры - гравитация - Общая теория относительности - решение Шварцшильда - решение Керра - белая дыра - сингулярность
Публикации со словами: черные дыры - гравитация - Общая теория относительности - решение Шварцшильда - решение Керра - белая дыра - сингулярность | |
См. также:
Все публикации на ту же тему >> | |