<< Титульный дист | Оглавление | 9. Геометрия решения Шварцшильда >>
8. Черные дыры
Еще в 1795 г. великий французский математик Пьер-Симон Лаплас теоретическим путем пришел к выводу, что свет не может уйти от тела, если оно достаточно массивно или достаточно сильно сжато. Даже из ньютоновской теории следует, что если скорость убегания для какого-либо объекта превышает величину скорости света, то этот объект для внешнего наблюдателя будет казаться абсолютно черным. Но на протяжении почти двухсот лет никому не приходило в голову, что в природе могут действительно существовать черные дыры. Однако к середине 1960-х годов астрофизикам удалось рассчитать подробно структуру звезд и ход их эволюции. Теперь, зная больше, астрономы отчетливо понимают,љ чтољ нељљ можетљљ существоватьљ устойчивыхљљ мертвых звезд, масса которых превышала бы три солнечные массы. Поскольку во Вселенной звезды, обладающие намного большими массами, - широко распространенное явление, астрофизики стали всерьез обсуждать возможность существования черных дыр, рассеянных повсюду во Вселенной.
Как мы узнали из предыдущей главы, черная дыра - это один из трех возможных вариантов конечной стадии эволюции звезд. Однако в отличие от белых карликов и нейтронных звезд черная дыра - это пустое место. Это то, что остается после катастрофического гравитационного коллапса массивной звезды, когда она умирает. При коллапсе - катастрофическом сжатии звезды - напряженность силы тяготения над ее поверхностью становится настолько чудовищно большой, что окружающее звезду пространство-время свертывается, и звезда исчезает из Вселенной; остается только исключительно сильно искривленная область пространства-времени.
Исследовать свойства черных дыр лучше всего, изучая, как движутся в этих сильно искривленных областях пространства-времени объекты - малые тела (материальные точки) и лучи света. Рассмотрим, например, черную дыру, изображенную на рис. 8.1. Представим себе, что на нее падают лучи света. Тот луч, который проходит очень далеко от черной дыры, отклоняется от своего обычного прямолинейного пути лишь совсем немного.

|
| Рис. 8.1. Как идут световые лучи вблизи черной дыры? Лучи света отклоняются мощным гравитационным полем, окружающим черную дыру. Вдали от дыры лучи искривляются слабо. Если же луч проходит совсем рядом с дырой, она может захватить его на круговую орбиту или засосать в себя совсем. |
Вдалеке от черной дыры пространство-время почти плоское, и там световые лучи распространяются прямолинейно. Это - важный факт. Утверждения в некоторых недавно опубликованных книжках, что черные дыры представляют угрозу для нас, совершенно неверны. Черные дыры не могут странствовать по Вселенной, "заглатывая" там и сям планеты, звезды и галактики. Всего в нескольких тысячах километров от черных дыр с массой в 10-20 солнечных масс пространство-время практически плоское и релятивистские эффекты несущественны. Если однажды ночью Солнце с помощью какого-либо волшебства превратится в черную дыру, вы будете спокойно спать в своей постели, не замечая ничего необычного, по крайней мере пока не наступит утро. Рассвет не наступит, но Земля будет продолжать двигаться по своей орбите с радиусом 150 миллионов километров, как она это делала все предыдущие пять миллиардов лет.
Возвращаясь к рис. 8.1, отметим, что лучи света, проходящие ближе к черной дыре, отклоняются на более значительные углы. Когда свет распространяется через область пространства-времени с большей кривизной, его мировая линия становится все более искривленной. Можно даже направить луч света точно в таком направлении относительно черной дыры, чтобы этот свет оказался пойман на круговую орбиту вокруг дыры. Эта сфера вокруг черной дыры иногда называется "фотонной сферой" или "фотонной окружностью"; она образована светом, обегающим вокруг черной дыры по всевозможным круговым орбитам. Каждая звезда во Вселенной посылает хоть немного света именно на такое расстояние от черной дыры, что этот свет захватывается на фотонную сферу.
Следует помнить, что эти круговые орбиты на фотонной сфере чрезвычайно неустойчивы. Чтобы понять смысл этого утверждения, представим себе почти круговую орбиту Земли вокруг Солнца. Орбита Земли устойчива. Если Землю слегка толкнуть то не случится ничего особенного. Однако если луч света хоть немного отклонится от своего идеального кругового пути на фотонной сфере, то он очень быстро уйдет по спирали либо внутрь черной дыры, либо обратно в космическое пространство. Самое ничтожное возмущение, куда бы оно ни было направлено -внутрь или наружу, уводит свет с фотонной сферы. Именно в этом смысле говорят о неустойчивости всех круговых орбит на фотонной сфере.
Наконец, те лучи света, которые нацелены почти прямо на черную дыру, "всасываются" в нее. Такие лучи навсегда уходят из внешнего мира - черная дыра их буквально поглощает.
Представленный здесь сценарий описывает поведение самого простого из возможных типов черных дыр. В 1916 г., всего через несколько месяцев после того как Эйнштейн опубликовал свои уравнения гравитационного поля, немецкий астроном Карл Шварцшильд нашел их точное решение, которое, как оказалось впоследствии, описывает геометрию пространства-времени вблизи идеальной черной дыры. Это решение Шварцшильда описывает сферически симметричную черную дыру, характеризующуюся только массой. Породившая эту черную дыру гипотетическая умирающая звезда должна не вращаться и быть лишенной как электрического заряда, так и магнитного поля. Вещество такой умирающей звезды падает по радиусу "вниз" к центру звезды, и говорят, что получившаяся черная дыра обладает сферической симметрией. Если бы черная дыра возникала при коллапсе вращающейся звезды, то у нее было бы некое "привилегированное" направление, а именно дыра обладала бы осью вращения. Решение Шварцшильда свободно от подобных усложнений. Такая шварцшильдовская черная дыра представляет собою самый простой из всех возможных тип черной дыры. В этой и в следующей главе мы ограничимся рассмотрением лишь этого простого случая. Последующие главы будут посвящены электрически заряженным и вращающимся черным дырам.
Понять природу шварцшильдовской черной дыры можно, рассматривая массивную (но не вращающуюся и не имеющую заряда) умирающую звезду в процессе гравитационного коллапса. Пусть некто стоит на поверхности такой умирающей звезды, у которой только что иссякло ядерное топливо (рис. 8.2). Непосредственно перед началом коллапса наш наблюдатель берет мощный прожектор и направляет его лучи в разные стороны. Так как вещество звезды пока распределено в достаточно большом объеме пространства, гравитационное поле у поверхности звезды остается довольно слабым. Поэтому луч прожектора распространяется прямолинейно или почти прямолинейно. Однако после начала коллапса вещество звезды сжимается во все меньшем и меньшем объеме. По мере уменьшения размеров звезды тяготение у ее поверхности возрастает все больше и больше. Увеличение кривизны пространства-времени приводит к отклонению светового луча от прежнего прямолинейного распространения. Сначала лучи, исходящие из прожектора под малым углом к горизонту, отклоняются вниз к поверхности звезды (см. рис. 8.2,6). Но в дальнейшем, по мере развития коллапса, нашему исследователю приходится направлять лучи вверх все ближе к вертикали, чтобы они могли навсегда уйти от звезды. В конце концов на некоторой критической стадии коллапса исследователь обнаружит, что уже никакой луч не в состоянии уйти от звезды. Как бы наш исследователь ни направлял свой прожектор, его луч все равно изменяет свое направление так, что снова падает вниз, на звезду. Тогда говорят, что звезда прошла свой горизонт событий. Ничто, очутившееся за горизонтом событий, не может выйти наружу, даже свет. Исследователь включает свой радиопередатчик и обнаруживает, что он ничего не может передать оставшимся снаружи, поскольку радиоволны не способны вырваться за горизонт событий. Наш исследователь буквально исчезает из внешней Вселенной.
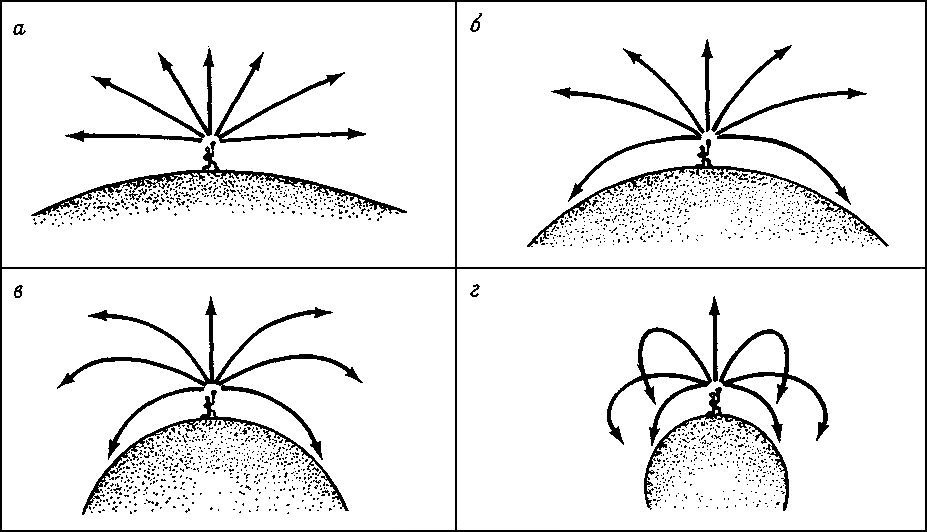
|
| Рис. 8.2 Как идут световые лучи от коллапсирующей звезды? Обреченный на гибель космонавт посылает лучи света с поверхности умирающей звезды. До начала коллапса (а) гравитационное поле было сравнительно слабым, и траектории световых лучей оказывались почти прямыми. На поздней стадии коллапса (г) пространство-время около звезды сильнейшим образом искривлено, и световые лучи отклоняются очень заметно. |
|
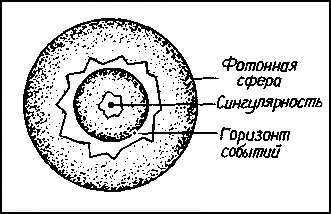
| Рис. 8.3. Шварцшильдовская черная дыра. Простейшая идеальная черная дыра (незаряженная и невращающаяся) окружена фотонной сферой. Сферический горизонт событий представляет собою "поверхность" черной дыры. В центре дыры находится сингулярность. |
Зная решение Шварцшильда, можно рассчитать положение горизонта событий, окружающего черную дыру. Например, поперечник сферы горизонта событий черной дыры с массой, равной 10 солнечным массам, составляет около 60 км. Как только умирающая звезда с массой в 10 солнечных масс сожмется до поперечника в 60 км, пространство-время столь сильно искривится, что вокруг звезды возникнет горизонт событий. В результате звезда исчезнет.
В момент, когда умирающая звезда уйдет за свой горизонт событий, ее размеры еще довольно велики, но никакие физические силы уже не смогут остановить ее дальнейшее сжатие. И звезда в целом продолжает сжиматься, пока, наконец, не прекратит свое существование в точке в центре черной дыры. В этой точке бесконечно давление, бесконечна плотность и бесконечна кривизна пространства-времени. Это "место" в пространстве-времени именуется сингулярностью.
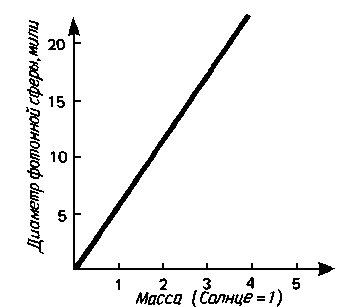
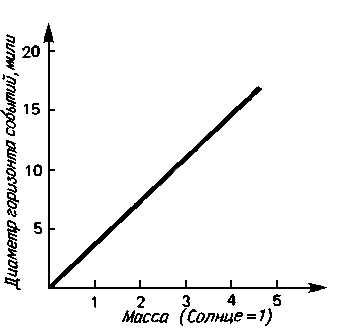
Данные о структуре шварцшильдовской черной дыры подытожены на рис. 8.3. Прежде всего черную дыру окружает фотонная сфера, состоящая из лучей света, движущихся по неустойчивым круговым орбитам. Внутри фотонной сферы находится горизонт событий - односторонне пропускающая поверхность в пространстве-времени, из которой ничто не может вырваться. Наконец, в центре черной дыры находится сингулярность. Все то, что проваливается сквозь горизонт событий, засасывается в сингулярность, где оно под действием бесконечно сильно искривленного пространства-времени прекращает свое существование. На рис. 8.4 и 8.5 показаны соответственно зависимости между массой черной дыры и поперечниками ее фотонной сферы и горизонта событий.
|
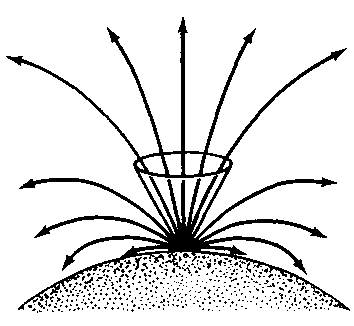
| Рис. 8.6. Конус выхода. С помощью этого воображаемого конуса удобно разделять световые лучи на способные покинуть звезду и на те лучи, которые она от себя не отпускает. Уйти в окружающую Вселенную удается только тем лучам, которые испущены с поверхности звезды под углами, заключенными во внутренней части конуса выхода. |
После того как умирающая звезда заходит за свою фотонную сферу и приближается к горизонту событий, от нее в окружающую Вселенную может вырваться все меньше и меньше световых лучей. Иллюстрированные на рис. 8.2 эффекты становятся все более заметными. Подобный захват лучей света коллапсирующей звездой можно описать с помощью воображаемого конуса, показанного на рис. 8.6 и называемого конусом выхода. Навсегда уйти от звезды могут только те лучи, которые покидают ее в пределах конуса выхода. Лучи же, идущие от поверхности звезды вне конуса выхода, отклоняются назад, к ее поверхности. По мере приближения катастрофического коллапса массивной звезды к его неизбежному концу, лучам света с поверхности звездыљљ становитсяљљ всељљ труднеељљ иљљ труднеељљ уйтиљ навсегдаљљ от звезды. Эти уходящие вовне лучи должны быть испущены внутри все более сужающегося конуса с осью, направленной вдоль вертикали. Иными словами, по мере того как звезда подходит к своему горизонту событий, конус выхода схлопывается. Непосредственно над границей фотонной сферы конус выхода широко раскрыт. От звезды могут уйти лучи света, испущенные под любыми углами. Но когда звезда подходит к своему горизонту событий, конус выхода становится настолько узким, что все лучи светаљљ вљљ концељљ концов љљзаворачиваютсяљљ назад,љљ кљљ поверхности звезды. Поведение конуса выхода дает первое важное указание на то, как должна выглядеть звезда, превращающаяся в черную дыру. По мере схлопывания конуса выхода от звезды уходит все меньше и меньше света. Поэтому астроном, наблюдающий подобную звезду издалека, видит ее все более и более слабой. Фактически такое убывание яркости умирающей звезды происходит очень быстро. Рассмотрим, например, образование черной дыры из звезды с массой в 10 солнечных масс. Как показано на рис. 8.7, с приближением поверхности звезды к горизонту событий ее яркость убывает с невероятной быстротой. Спустя всего 1/1000 с после начала гравитационного коллапса конус выхода становится настолько узким, что лишь одна квадрильонная (10-15!) света звезды может ускользнуть во внешнюю Вселенную. Всего миг - и бывшая яркая звезда становится почти совершенно черной!
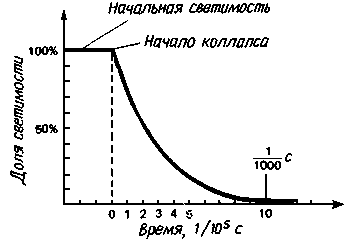
|
| Рис. 8.7. Светимость коллапсирующей звезды. Сразу после начала конечного этапа коллапса звезда становится чрезвычайно слабой за очень короткий промежуток времени. График построен для звезды с массой 10 солнечных. Всего через 1/1000 с светимость звезды падает до 2% первоначальной, а спустя 1/100 с она составляет менее одной квадрильонной (10-15) первоначальной. |
Замедление хода времени, которое почти невозможно заметить в слабом гравитационном поле Земли, становится в процессе образования черной дыры фактором фундаментальной важности. Ведь на самом горизонте событий течение времени полностью останавливается (рис. 8.8). При объяснении этого утверждения нужно быть очень осторожным. Проиллюстрируем ситуацию, вообразив, что мы бросили в черную дыру камень. Допустим, вы выпустили этот камень из рук, находясь очень далеко от черной дыры, где пространство-время почти плоское. Наблюдая движение камня, мы увидим, что по мере приближения к черной дыре он падает все быстрее и быстрее. Если бы была верна ньютоновская теория, то наш камень продолжал бы увеличивать скорость, и в тот момент, когда он врезался бы в сингулярность, он двигался бы практически с бесконечной скоростью. Но в столь сильных гравитационных полях ньютоновская теория не может давать правильных ответов. Оказывается, когда камень подлетает к горизонту событий, начинает преобладать действие замедления времени. Вы обнаружите, к своему удивлению, что камень начинает падать все медленнее и совсем останавливается на горизонте событий, потому что на этом горизонте для внешнего наблюдателя перестает течь время. Оставаясь вдалеке от черной дыры, мы должны прождать бесконечно долгий промежуток времени, чтобы увидеть, как камень пересечет горизонт событий.
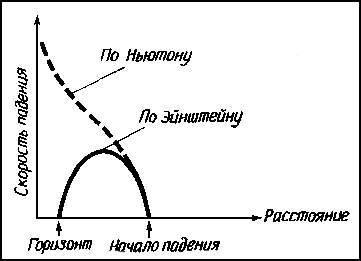
|
| Рис. 8.8. Скорость тела при свободном падении. Удаленный наблюдатель видит, что свободное падение тела на черную дыру замедляется по мере того, как оно приближается к горизонту событий. Кажется, что на горизонте событий тело "застывает", ибо там останавливается течение времени. |
в одной и той же пропорции, включая его пульс, его процессы мышления и темп, в котором он стареет. Согласно утверждению удаленного наблюдателя, космонавт, падающий на черную дыру, никогда не достигнет горизонта событий; он останется живым навсегда в преддверии вступления в черную дыру в состоянии замедленной жизнедеятельности, и ему потребуются многие миллиарды лет, чтобы преодолеть те несколько сантиметров, которые отделяют его от горизонта событий. Однако, согласно данным падающего наблюдателя, его часы отсчитывают время в своем обычном темпе. Поэтому он проскакивает за горизонт событий спустя весьма краткий срок, если судить по его часам. Однако сразу после прохождения через горизонт событий он обнаруживает нечто неладное. Подобно тому как на горизонте событий остановилось время для внешнего наблюдателя, внутри горизонта оно меняется ролями с пространством. Вдали от черной дыры, скажем у нас на Земле, человек способен перемещаться в трех пространственных измерениях (вверх и вниз, налево и направо, вперед и назад). Однако во временном измерении мы бессильны "ходить" туда и обратно. Мы безостановочно идем вперед во времени - от нашего рождения к старости и к смерти, хотим мы этого или нет. Внутри же горизонта событий роли пространства и времени меняются. Зло-частный космонавт, попавший под горизонт событий, начинает безостановочно увлекаться вперед в пространстве навстречу сингулярности! Он бессилен избежать рокового столкновения с сингулярностью. На рис. 8.9 показано, сколько времени может, самое большее, пройти по часам космонавта между моментами пересечения горизонта и прихода в сингулярность. Что бы он ни предпринимал, даже имея в своем распоряжении наимощнейшие ракетные двигатели, он должен попасть в сингулярность спустя промежуток времени, не меньший, чем указано на этом графике. Например, пройдя под горизонт черной дыры с массой 6,5 солнечной массы, космонавт должен достигнуть сингулярности менее чем за 1/1000 с.
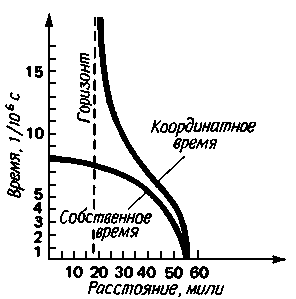
Чтобы избежать путаницы, связанной с измерением времени, физики вводят два типа времени. Координатное время - это то время, которое измеряет наблюдатель, находящийся далеко от черной дыры (т.е. в плоском пространстве-времени). Собственное время - это то время, которое измеряет по своим часам свободно падающий наблюдатель. Времена эти разные. В координатном времени камню, брошенному в черную дыру, нужно лететь миллионы миллионов лет, чтобы приблизиться к горизонту событий. В собственном же времени, по часам, привязанным к падающему камню, последний уже через короткий промежуток времени пересечет этот горизонт. На рис. 8.10 сопоставлены промежутки координатного и собственного времен, в течение которых тело падает на черную дыру с массой 10 солнечных масс с начального расстояния 90 км.
|
|
Что касается человека, падающего на черную дыру, то следует уделить внимание и другим любопытным эффектам. Предположим, что вы падаете вниз ногами к черной дыре. Ваше падение все время свободное, так что вы находитесь в состоянии невесомости. Однако при сближении с черной дырой вы начнете ощущать нечто необычное, поскольку ваши ноги оказываются ближе к черной дыре, чем ваша голова. Дело в том, что ваши ноги будут падать быстрее, чем голова. В результате вас станет вытягивать в длинную тонкую нить. К моменту пересечения горизонта ваша длина может достичь сотни километров. Как видите, падение на черную дыру-занятие не из приятных. И в самом деле, еще задолго до того, как вы приблизитесь к фотонной сфере, ваше тело будет разорвано приливными силами невероятной мощи. Общая картина представлена на рис. 8.11.
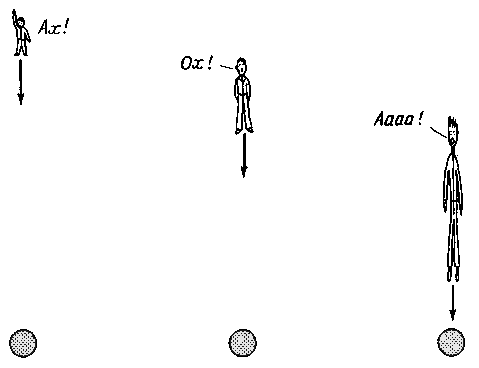
|
| Рис. 8.11. Приливные силы.љ При падении наљ чернуюљ дыруљ наблюдатель растягивается и разрывается на части огромными приливными силами. |
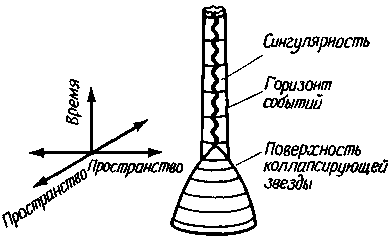
|
| Рис. 8.12. Образование черной дыры. После того как в области с поперечником меньше 2 шварцшильдовских радиусов соберется достаточное количество вещества, вокруг последнего возникает горизонт событий. Затем захваченное вещество быстро падает на сингулярность в центре черной дыры. |
Разобраться в структуре черных дыр удобнее всего, представив себе воображаемое путешествие на космическом корабле, оборудованном большими смотровыми иллюминаторами. В ряде следующих глав мы используем такую "технику" и сможем узнать, что увидели бы бесстрашные астрономы, если бы они действительно отправились в путешествие к различным типам черных дыр, в сами эти дыры и даже сквозь них.
Вообразимљљљ себељљљ космическийљљљ корабль,љљљ показанныйљљљ на рис. 8.13. Он снабжен двумя большими иллюминаторами. Носовой иллюминатор смотрит прямо в центр черной дыры, а кормовой - в противоположном направлении, позволяя обозревать окружающую Вселенную. Из каждого иллюминатора видна в точности половина всего неба. Кроме того, наш космический корабль обладает очень мощными ракетными двигателями, позволяющими ему удерживаться на разных высотах над горизонтом событий. На борту корабля находятся два астронома, которые фотографируют с различных расстояний от черной дыры все, что им видно из иллюминаторов.
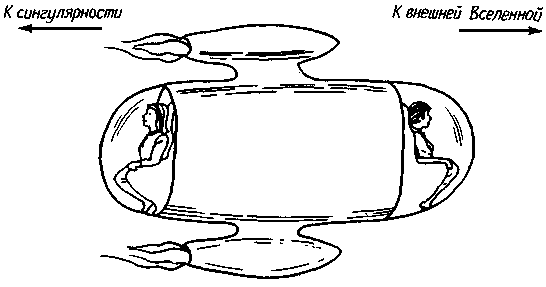
|
| Рис. 8.13. Космический корабль. Два любознательных астронома решили выяснить, как же в действительности выглядит черная дыра. Для этого они построили космический корабль, снабженный двумя иллюминаторами. Носовой иллюминатор обращен прямо на середину черной дыры, а кормовой направлен во внешнюю Вселенную. Из каждого иллюминатора видна в точности половина небесной сферы. Корабль оборудован также мощными реактивными двигателями, с помощью которых космонавты могут зависать над черной дырой на разных высотах. |
Для удобства наши космические астрономы выражают свое расстояние от черной дыры в шварцшильдовских радиусах, а не милях или километрах. Вспомним, что шварцшильдовский радиус - это радиус горизонта событий. Чем массивнее черная дыра, тем больше ее шварцшильдовский радиус. В табл. 8.1 приведены значения шварцшильдовского радиуса черных дыр, обладающих разными массами.
Эта таблица тесно связана с рис. 8.5. Поперечник горизонта событий черной дыры - это в точности удвоенная величина ее шварцшильдовского радиуса. Далее, раз поперечник горизонта событий равен удвоенному шварцшильдовскому радиусу, то поперечник фотонной сферы - это утроенный шварцшильдовский радиус.
|
Таблица 8.1 | ||||||||||||||||||||||||||||||||||||||
|
Шварцшильдовские радиусы черных дыр,
| ||||||||||||||||||||||||||||||||||||||
|
Путешествие двух астрономов на нашем воображаемом космическом корабле начинается с того, что этому уникальному кораблю предоставляется возможность просто падать на черную дыру вдоль ее радиуса. На разных этапах сближения с дырой космонавты включают мощные ракетные двигатели, которые мгновенно останавливают падение корабля. В эти моменты покоя астрономы делают два снимка - один из носового иллюминатора (вид в сторону черной дыры), а другой - из кормового (вид назад на Вселенную). Корабль останавливался пять раз, и всякий раз делалась пара фотографий:
| Снимок | Расстояние от черной дыры | |
| Фото А: | Расстояние велико (много шварцшильдовских радиусов) | |
| Фото Б: | 5 шварцшильдовских радиусов | |
| Фото В: | 2 шварцшильдовских радиуса | |
| Фото Г: | На фотонной сфере (1.5 шварцшильдовского радиуса) | Прямо над горизонтом событий (чуть больше 1 шварцшильдовского радиуса) |
На рис. 8.14 показано, где был космический корабль относительно черной дыры в моменты получения снимков.
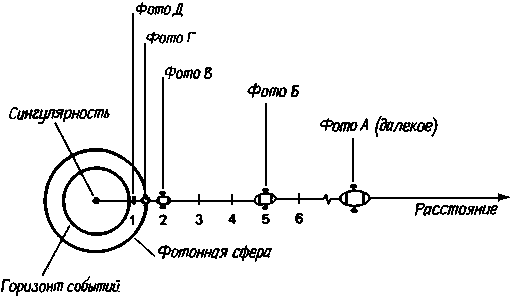
|
| Рис. 8.14. Приближение космического корабля к черной дыре. Пять пар фотографий шварцшильдовской черной дыры сняты из указанных на рисунке точек. |
На очень больших расстояниях от черной дыры сама дыра выглядела как маленькое пятно света в середине носового иллюминатора (рис. 8.15,А). Окружающее небо оставалось практически неискаженным, за одним важным исключением. Все звезды во Вселенной посылают хоть немного света в окрестности фотонной сферы. Этот свет кружит вокруг черной дыры раз-другой или больше, а затем его траектория раскручивается спиралью навстречу космическому кораблю. Поэтому астроном, проводящий наблюдения через носовой иллюминатор, видит многократные изображения всех звезд Вселенной, обрамляющие видимый "край" черной дыры. (Чтобы рис. 8.15,А-Д не получились перегруженными, все эти многократные изображения опущены.) Таким образом, вид неба около черной дыры будет весьма сложным и искаженным.
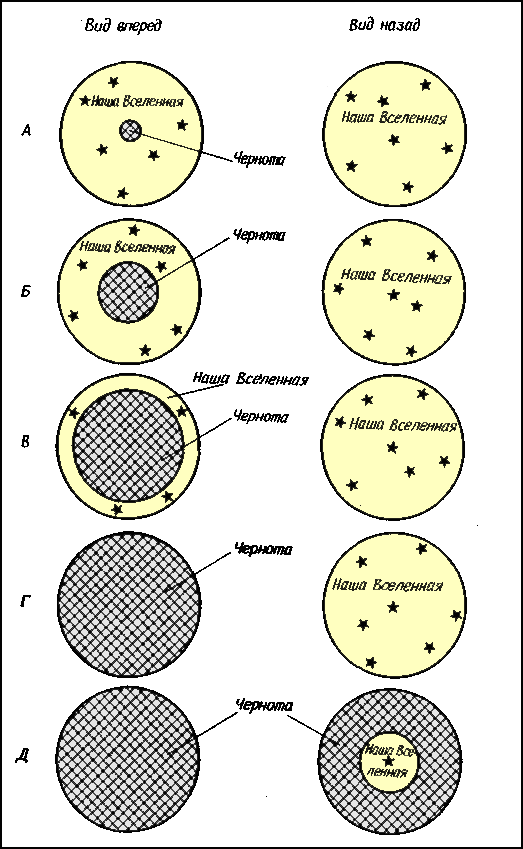
|
Рис. 8.15.
Фото А: (вид издалека от
черной дыры). Расстояние от черной дыры равно многим шварцшильдовским
радиусам. Черная дыра выглядит отсюда как маленькое черное пятнышко в центре
поля зрения носового иллюминатора.
|
В 1975 г. Кэннингэм из Калифорнийского технологического института (США) провел ряд расчетов, которые помогли выяснить, как выглядит черная дыра, если глядеть на нее с разных расстояний. Рис. 8.15,Б показывает (на основании этих вычислений), что будет видно с расстояния в 5 шварцшильдовских радиусов. Так как космический корабль в этом случае находится вблизи черной дыры, она представляется большей, чем на рис. 8.15,А. На расстоянии в 5 шварцшильдовских радиусов (что соответствует расстоянию 150 км, если черная дыра имеет массу в 10 солнечных масс) угловой поперечник дыры равен примерно 56њ. Вид же из кормового иллюминатора остается практически неискаженным.
С расстояния в 2 шварцшильдовских радиуса (60 км от черной дыры в 10 раз более массивной, чем Солнце) черная дыра - основной объект в небе перед космическим кораблем. Ее угловой поперечник вырос уже до 136њ (рис. 8.15,В). Все видимое вокруг нее из носового иллюминатора небо чрезвычайно сильно искажено и заполнено многократными изображениями огромного количества звезд и галактик. Даже из кормового иллюминатора небо наблюдается уже сильно искаженным.
С "высоты" фотонной сферы (45 км от черной дыры в 10 раз массивней Солнца) изображение черной дыры занимает все поле зрения носового иллюминатора космического корабля, как видно на рис. 8.15,Г. По краям поля зрения кормового иллюминатора теперь видны бесчисленные многократные изображения.
По мере дальнейшего приближения космического корабля к горизонту событий черная дыра начинает просматриваться по краям поля зрения кормового иллюминатора. Вся внешняя Вселенная видна теперь как маленький кружок в центре кормового иллюминатора (рис. 8.15,Д). Размеры этого кружка определяются углом раствора конуса выхода, о котором мы упоминали выше. На самом горизонте событий (это примерно в 30 км от центра черной дыры в 10 раз более массивной, чем Солнце), где конус схлопывается, все звезды неба собираются в одной точке в центре поля зрения кормового иллюминатора.
Вспомним, что наш космический корабль снабжен мощными ракетными двигателями, способными остановить его падение на разных расстояниях от черной дыры, так что астрономы могут не спеша вести свои наблюдения. Однако гравитационное поле черной дыры настолько мощное, что уже на расстоянии нескольких шварцшильдовских радиусов двигатели ракеты должны работать на полную мощность. Еще задолго до того, как астрономы доберутся до точки, из которой они смогли бы сделать снимок Б, им придется испытать действие ускорения, составляющего тысячи g, которое буквально расплющит их о переборки корабля.
Чтобы избежать подобной участи, другие два астронома принимают решение совершить свободное падение на черную дыру до конца. Их космический корабль новейшей конструкции вообще лишен ракетных двигателей, которые замедляли бы его падение. Более того, чтобы избежать разрывающего действия приливных сил, произведена микроминиатюризация как космического корабля, так и самих космонавтов. Тем не менее они понимают, что и такая экспедиция равносильна самоубийству, ибо, попав под горизонт событий, они будут обречены упасть на сингулярность. Эти новые два астронома видят из иллюминаторов своего обреченного на гибель космического корабля совершенно иную картину. Однако, чтобы понять смысл этой картины, нам придется сначала рассмотреть вопрос о природе шварцшильдовской геометрии.
<< Титульный дист | Оглавление | 9. Геометрия решения Шварцшильда >>
|
Публикации с ключевыми словами:
черные дыры - гравитация - Общая теория относительности - решение Шварцшильда - решение Керра - белая дыра - сингулярность
Публикации со словами: черные дыры - гравитация - Общая теория относительности - решение Шварцшильда - решение Керра - белая дыра - сингулярность | |
См. также:
Все публикации на ту же тему >> | |