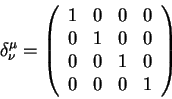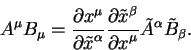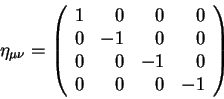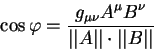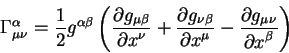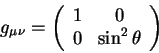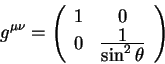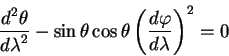<< 4. Эксперименты по ОТО | Оглавление | 6. Анализ в неэвклидовой >>
5. Неэвклидова геометрия
В классической физике пространство было эвклидовым, а время абсолютным и единым для всего пространства. В релятивистской физике, как мы уже убедились из материала предыдущей главы пространство является неэвклидовым. В общем случае геометрия представляет из себя четырехмерное дифференцируемое многообразие,
В произвольной геометрии рассматриваются произвольные преобразования
координат:
например,

как видно из приведенных преобразований, они описывают просто переход от сферических к декартовым координатам.
Дифференциал в нетильдованной системе связан с дифференциалом в системе
координат с тильдой уравнениями вида:
В геометрии вводится понятие геометрического объекта. Не перечисляя всех объектов геометрии назовем только скаляры, векторы и тензоры. Строго говоря, все перечисленные величины являются тензорами, так скаляр является тензором нулевого ранга, а вектор тензором первого ранга. Однако исторически принято выделять скаляры и векторы.
Скалярная величина (или скаляр) при преобразованиях системы координат не
преобразуется,
Вектором называется величина, которая содержит четыре компоненты,
преобразуемые согласно правилу:
для контравариантных компонент и
для ковариантных компонент.
Как можно заметить, из закона преобразования (5.1) преобразование контравариантных компонент какого - либо вектора подобно преобразованию дифференциалов координат, представляющих разность положений двух точек. Следовательно контравариантные компоненты вектора можно представить как систему из двух точек, с указанием какая из точек является первой, а какая является второй. Примером контравариантных компонент является четырехмерная скорость какого - либо тела.
Примером ковариантных компонет вектора является градиент некоторого поля:
Образом градиента от поля являются наборы двумерных поверхностей
определяющих постоянство поля
![]() . Следовательно
геометрическим образом ковариантных компонент тензора являются двумерные
поверхности "раскрашенные" в различные "цвета" для того, чтобы определить
какая из поверхностей является первой, а какая - второй.
. Следовательно
геометрическим образом ковариантных компонент тензора являются двумерные
поверхности "раскрашенные" в различные "цвета" для того, чтобы определить
какая из поверхностей является первой, а какая - второй.
Выпишем также правило по которому преобразуются компоненты тензора второго
ранга:

Геометрическая величина
![]() , которая имеет
, которая имеет ![]() верхних ипндексов и
верхних ипндексов и ![]() нижних
индексов и преобразуется по закону:
нижних
индексов и преобразуется по закону:
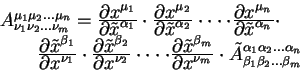
называется тензором ранга ![]() с
с ![]() контравариантными
контравариантными ![]() ковариантными
индексами.
ковариантными
индексами.
В алгебре тензоров определяется суммирование тензоров одинакового ранга и с
одинаково расположенными индексами:
умножение определено для тензоров любого ранга с произвольно расположенными
индексами:
В тензорной алгебре определяют также свертку двух тензоров по правилу:
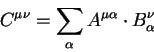
для произвольного расположения индексов важно только, чтобы индекс по
которому проводится свертка в первом тензоре был верхним, во втором -
нижним (или наоборот, в первом - нижним, а во втором -верхним). Положение и
количество остальных индексов переносится в свертку по их месту. Свертки
могут быть образованы различными способами, однако каждое суммирование
должно выполняться по верхнему и нижнему индексу. Например, сумма

не является тензором, как легко убедиться рассмотрев закон преобразования этой величины.
В современной тензорной алгебре, анализе и физике пользуются правилом
суммирования Эйнштейна, который для удобства ввел следущее обозначение:
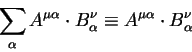
при этом индекс ![]() называют мертвым индексом и по повторяющимся
индексам производится суммирование. Так запись
называют мертвым индексом и по повторяющимся
индексам производится суммирование. Так запись
![]() обозначает:
обозначает:
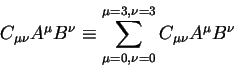
Повсюду в этой книге мы будем использовать это правило, два повторяющихся индекса один верхний, другой - нижний будет означать, что по ним производится суммирование.
Определим также обратные тензоры согласно уравнению:
Здесь
![]() - символ Кронекера, который определяется
следущими условиями
- символ Кронекера, который определяется
следущими условиями
![]() если
если ![]() и
и
![]() если
если ![]() . Можнл также выписать матрицу
символа Кронекера
. Можнл также выписать матрицу
символа Кронекера
Свертка двух тензоров понижает ранг произведения. Так, важный пример
показывает, что произведение ковариантных компонент вектора на
контравариантные компоненты является инвариантом:
Различные авторы [8], [9], [12] вводят также операцию симметрирования, албтернирования, выключения индексов и т.п. Для нас важной остается только последняя операция над тензорами - образование следа, образование поперечной части тензора и образование поперечно - бесследовой части тензора, которые будут применяться во второй части книги. Однако для их определения нам придется использовать метрику, поэтому отложим введения этих понятий после обсуждения метрики.
5.1 Метрика искривленного пространства - времени
Геометрия четырехмерного пространства - времени полностью определяется десятью функциями, которые являются компонентами симметричного тензора второго ранга. Метрика четырехмерного интервала есть:
Здесь ![]() - ковариантные компоненты метрического тензора или, как
обычно говорят, метрический тензор второго ранга.
- ковариантные компоненты метрического тензора или, как
обычно говорят, метрический тензор второго ранга.
Компоненты метрического тензора являются, вообще говоря, функциями всех четырех координат.
Преобразованием координат всегда можно добиться того, чтобы компоненты
метрического тензора были приведены к виду метрики Минковского:
В пространстве с заданной метрикой можно определить связь между
ковариантными и контравариантными компонентами тензоров, так для вектора
связь между этими компонентами задается уравнениями:
Теперь можно определить норму вектора, аналогично тому, как это делается в
эвклидовой геометрии. Норомой вектора по определению полагают величину
[8], [9], [12]:
В зависимости от того, чему равна норма ветора его называют:
- времениподобным, если
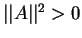
- пространственноподобным, если
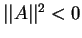
- изотропным, если
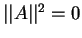
Норма называется также длиной вектора. Как видно из определения изотропного вектора он обладает нулевой длиной.
Рассмотрим свертку двух векторов. Два вектора, которые удовлетворяют
условию:
называются ортогональными. Отсюда можно сделать вывод, что изотропный вектор ортогонален самому себе и любому другому изотропному вектору. Следует заметить, что таким свойством обладают только изотропные вектора.
Кроме этого важного свойства приведем также уравнение описывающее угол
![]() между двумя векторами
между двумя векторами ![]() и
и ![]() в неэвклидовой
геометрии:
в неэвклидовой
геометрии:
Здесь следует заметить, что оба вектора ![]() и
и ![]() являются либо
пространственноподобными, либо изотропными.
являются либо
пространственноподобными, либо изотропными.
5.1.1 Примеры метрики искривленного пространства
Приведем примеры метрики искривленного пространства. На самом деле в быту мы сталкиваемся с примера геометрии искривленного пространства значительно чаще, чем привыкли думать. Поверхность мяча, поверхность спинки кресла, поверхность кувшина или графина - вот неполный список двумерных искривленных пространств. Примеры идеальных плоскостей, таких как крышка стола или ровный листок бумаги в этом ряду выглядят, скорее исключениями, чем правилом.
Приведем в качестве примера метрику на поверхности сферы. Для этого выпишем
вначале метрику эвклидова пространства в сферической системе координат:
Будем считать, что мы вычисляем расстояние только между теми точками,
которые лежат на поверхности сферы радиуса ![]() . Тогда можно полагать, что
. Тогда можно полагать, что
![]() , а значит метрика получает вид:
, а значит метрика получает вид:
теперь метрика описывает поверхность сферы, а геометрия, которую описывает данный метрический тензор является неэвклидовой.
5.2 Геодезические линии в неэвклидовой геометрии
В эвклидовой геометрии очень важным понятием является прямая между двумя точками, которая к тому же является кратчайшим расстоянием между этими точками. В неэвклидовой геометрии понятие прямой заменяется понятием геодезической линии, которая является экстремальным путем между двумя точками.
Для нахождения уравнения геодезической линиии применим вариационное исчисление.
Длина линии в геометрии общей теории относительности есть интеграл по
интервалу между двумя событиями разделенными по времени и пространству:
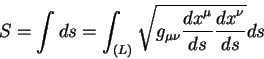
Линии экстремального пути удовлетворяет условию:
Здесь символ ![]() означает первую вариацию. Из этого условия
получается уравнение геодезической линии.
означает первую вариацию. Из этого условия
получается уравнение геодезической линии.
Для вычисления вариации величины ![]() применим следущий прием.
Проварьируем не дифференциал интервала
применим следущий прием.
Проварьируем не дифференциал интервала ![]() , а квадрат дифференциала
, а квадрат дифференциала
![]() . Вариации самого дифференциала по вариациям квадрата можно получить
согласно уравнению
. Вариации самого дифференциала по вариациям квадрата можно получить
согласно уравнению
![]() . С другой стороны,
вариации квадрата
. С другой стороны,
вариации квадрата ![]() есть:
есть:
правую часть этого равенства можно представить в виде суммы:
Воспользуемся равенствами
![]() и
и
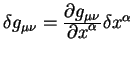 и получим уравнение для вариации дифференциала интервала:
и получим уравнение для вариации дифференциала интервала:
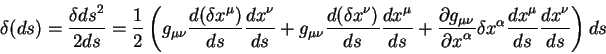
Третий член в круглых скобках уже приведен к виду пригодному для вычисления
первой вариации. Для приведения к такому же виду первых двух членов
воспользуемся равенством:
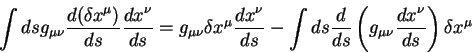
Воспользуемся теперь этими равенствами и вычислим первую вариацию полного
пути:
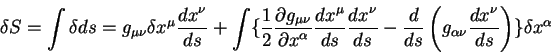
В этом уравнении первый член после второго знака равенства представляет из
себя вариации в конечных точках пути, по определению эти вариации равны
нулю [13], [14]. Член под знаком интеграла в фигурных скобках
должен обращаться в нуль на геодезической линии. Это и дает нам уравнение
геодезической линии:
Здесь ![]() - вектор касательный к геодезической линии.
- вектор касательный к геодезической линии.
Уравнение, которое мы получили является уравнением второго порядка. В
случае эвклидовой геометрии, когда все компоненты метрического тензора
являются диагональными и равны единице, правая часть равенства
(5.10) равна нулю. Тогда решение этого уравнения есть
![]() . Это решение описывает прямые линии, которые являются линиями
кратчайшего пути в эвклидовой геометрии.
. Это решение описывает прямые линии, которые являются линиями
кратчайшего пути в эвклидовой геометрии.
Приведем это уравнение к стандартной форме, принятой в неэвклидовой
геометрии. Для этого воспользуемся тождеством:
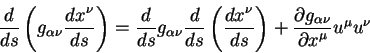
Подставив его в левую часть уравнения (5.10) получаем уравнение
вида:
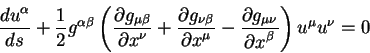
Величина
называется символом Кристоффеля. Символ Кристоффеля имеет три индекса и не является тензором. В алгебре такие величины носят название символы первого рода.
Стандартный вид уравнения геодезической линии в неэвклидовой геометрии
записывается с помощью символа Кристоффеля:
Кроме этого, стандартного вида уравнения геодезической линии, можно также
записать как меняется дифференциал касательного вектора ![]() при
переносе вдоль геодезической линии:
при
переносе вдоль геодезической линии:
5.2.1 Геодезические линии на поверхности сферы
Рассмотрим в качестве примера геодезические линии на сфере - двумерной
неэвклидовой поверхности. Метрический тензор на поверхности сферы имеет
вид:
Контравариантные компоненты метрического тензора на поверхности сферы есть:
Вычисляя символ Кристоффеля получаем, что все компоненты равны нулю за
исключением двух:

Уравнения геодезических линий имеют вид:
и
Здесь ![]() ,
, ![]() сферические координаты наклонения и азимута, а
сферические координаты наклонения и азимута, а
![]() - афинный параметр вдоль геодезической линии.
- афинный параметр вдоль геодезической линии.
При приведении к первому интегралу уравнение (5.17) получает вид:
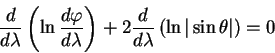
или
Здесь
 обозначает константу
интегрирования. Первый интеграл уравнения (5.16) можно легко
привести к удобной форме, если выбрать в качестве афинного параметра длину
вдоль геодезической
обозначает константу
интегрирования. Первый интеграл уравнения (5.16) можно легко
привести к удобной форме, если выбрать в качестве афинного параметра длину
вдоль геодезической
![]() . Тогда интеграл первого уравнения
становится:
. Тогда интеграл первого уравнения
становится:
Рассмотрим два частных случая геодезических линий.
Движение по экватору
Пусть наша линия начинается на экваторе
![]() , причем
направление этой линии совпадает с направлением экватора, т.е.
, причем
направление этой линии совпадает с направлением экватора, т.е.
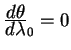 и
и
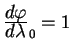 .
.
Решение для геодезической линии получается из уравнений (5.18,
5.19). Действительно, правая часть равенства (5.18)
есть 1. Подставляем выражение для
![]() в
уравнение (5.19) и получаем уравнение:
в
уравнение (5.19) и получаем уравнение:
Удовлетворяет этому уравнению только значения
![]() .
Таким образом доказано, что экватор является геодезической линией на сфере.
.
Таким образом доказано, что экватор является геодезической линией на сфере.
Движение по меридиану
Рассмотрим теперь движение вдоль меридиана и покажем, что меридиан также
является геодезической линией. Теперь вектор, касательный к линии имеет
компоненты:
Начальную точку также выберем на экваторе
![]() . Из
уравнения (5.18) получаем, что
. Из
уравнения (5.18) получаем, что
откуда следует, что
![]() . Из второго интеграла
системы (5.19) получаем, что
. Из второго интеграла
системы (5.19) получаем, что
откуда непосредственно следует, что
Не рассматривая общего случая решения системы (5.18, 5.19) упомянем только, что экватор и меридиан на поверхности сферы являются частными случаями большого круга - сечения поверхности сферы плоскостью, которая проходит через центр сферы. Рассматривая трехмерные вращения, можно показать, что только отрезок большого круга на сфере представляет кусок геодезической линии. Полная геодезическая линия представляет из себя большой круг.
Движение по малому кругу
Продемонстрируем отличие произвольной линии от геодезической линии на примере малого круга на сфере. Малый круг на сфере - это сечение сферы плоскостью, которая не проходит через центр сферы.
Выберем малый круг так, чтобы он был сечением с
![]() . Тогда
уравнения, которые описывают малый круг есть:
. Тогда
уравнения, которые описывают малый круг есть:
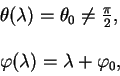
отсюда легко найти первые и вторые производные от координат по афинному
параметру:
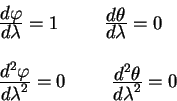
Подставляя эти значения в уравнения геодезических приходим к противоречию:
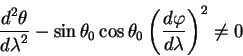
Таким образом малый круг на сфере не является геодезической линией.
<< 4. Эксперименты по ОТО | Оглавление | 6. Анализ в неэвклидовой >>
|
Публикации с ключевыми словами:
Общая теория относительности - специальная теория относительности - системы отсчета - измерение времени
Публикации со словами: Общая теория относительности - специальная теория относительности - системы отсчета - измерение времени | |
См. также:
Все публикации на ту же тему >> | |