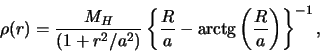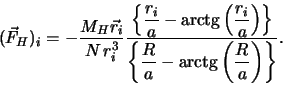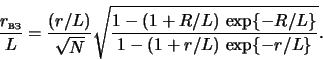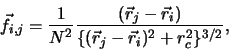<< 3. Моделирование звездных дисков | Оглавление | 3.2 Крупномасштабная структура ... >>
- 3.1.1 Модели типа "частица-частица" (PP)
- 3.1.2 Принцип построения экспериментальных моделей плоских галактик
- 3.1.3 Модели типа "частица-сетка" (PM)
- 3.1.4 Иерархические модели (TREE-модели)
3.1 Модели
Методов прямого лабораторного моделирования коллективных процессов в непрерывной или дискретной гравитирующей среде пока не существует. Вряд ли они будут разработаны и в обозримом будущем. Но появление достаточно мощных ЭВМ открыло уникальную возможность численного моделирования таких явлений и тем самым создало своеобразную экспериментальную базу для физики коллективных процессов в гравитирующих системах. В приложении к плоским галактикам такое моделирование может иметь целью определение темпа коллективных релаксационных процессов и направления эволюционных изменений тех или иных параметров диска, выяснение пространственной структуры квазистационарных плоских галактик и отдельных их подсистем, а также изучение тех процессов, которые могли бы привести к образованию таких наблюдаемых структур, как спиральные узоры, бары, особенности во взаимодействующих галактиках и т.п.
Практически устоявшимся термином для обозначения численного
моделирования гравитирующих ![]() тел (как, впрочем, и
газодинамических систем) стало словосочетание "численный (или
компьютерный) эксперимент". Численный эксперимент в последние годы
становится одним из основных инструментов в руках теоретиков при
изучении динамики звездных систем. Наблюдается буквально "золотая
лихорадка", характеризующаяся взрывным ростом числа публикаций. В то же
время, поскольку число нерешенных
еще задач существенно больше рассмотренных, то в основе полученных
результатов лежит обычно небольшая серия расчетов одной группы
исследователей. Как представляется, имеется насущная необходимость
повторения полученных ранее результатов, чтобы с большим доверием
к ним относиться, как это и принято в экспериментальной физике.
тел (как, впрочем, и
газодинамических систем) стало словосочетание "численный (или
компьютерный) эксперимент". Численный эксперимент в последние годы
становится одним из основных инструментов в руках теоретиков при
изучении динамики звездных систем. Наблюдается буквально "золотая
лихорадка", характеризующаяся взрывным ростом числа публикаций. В то же
время, поскольку число нерешенных
еще задач существенно больше рассмотренных, то в основе полученных
результатов лежит обычно небольшая серия расчетов одной группы
исследователей. Как представляется, имеется насущная необходимость
повторения полученных ранее результатов, чтобы с большим доверием
к ним относиться, как это и принято в экспериментальной физике.
Обычно используют два типа численных моделей звездного диска: модель "частица-частица" (PP); модель "частица-сетка" (PM) и ее различные модификации [241,242].
3.1.1 Модели типа "частица-частица"
(PP)
В моделях типа "частица-частица" используется непрерывное
описание движения частиц и в них учитывается гравитационное
взаимодействие всех частиц друг с другом. Такой метод, основанный
на прямом интегрировании уравнений движения для системы из
![]() частиц, является достаточно простым для понимания и реализации,
однако он требует больших машинных ресурсов. Поэтому в моделях
такого типа число частиц, как правило, не превышает
значений3.1
частиц, является достаточно простым для понимания и реализации,
однако он требует больших машинных ресурсов. Поэтому в моделях
такого типа число частиц, как правило, не превышает
значений3.1
![]() . Число арифметических действий,
необходимых для интегрирования одного временного шага в рамках модели
PP, равно
. Число арифметических действий,
необходимых для интегрирования одного временного шага в рамках модели
PP, равно
![]() . Нетрудно оценить, что при использовании
ЭВМ, для которой необходима 1 мкс
на выполнение одной операции,
при
. Нетрудно оценить, что при использовании
ЭВМ, для которой необходима 1 мкс
на выполнение одной операции,
при ![]() на один временной шаг (а всего их требуется, как правило,
несколько тысяч) затрачивается 10 с, а при
на один временной шаг (а всего их требуется, как правило,
несколько тысяч) затрачивается 10 с, а при ![]() больше суток!
больше суток!
Модели PP использовались в экспериментах [216-218,243-247] и
многих других. В этих моделях, однако, возникает
вопрос о величине масштаба и характере "обрезания" гравитационного
взаимодействия частиц на малых расстояниях. Дело в том, что при
моделировании полной галактики, состоящей из
![]() звезд, необходимо создать бесстолкновительную систему. Время двойного
соударения в трехмерной системе равно [61]
звезд, необходимо создать бесстолкновительную систему. Время двойного
соударения в трехмерной системе равно [61]
3.1.2 Принцип построения экспериментальных моделей плоских галактик
Опишем здесь достаточно простую модель с обоснованием выбора масштаба "обрезания" гравитационного взаимодействия на малых расстояниях.
1. Диск. Звездный диск полагаем состоящим из N
частиц равной массы. Используем систему единиц, в которой гравитационная
постоянная ![]() , все частицы диска распределены в начальный
момент времени внутри сферы радиусом
, все частицы диска распределены в начальный
момент времени внутри сферы радиусом ![]() и масса диска
и масса диска
![]() (масса каждой частицы равна
(масса каждой частицы равна ![]() ).
).
Выбрав закон изменения поверхностной плотности ![]() ,
разобьем диск на достаточно узкие кольца шириной
,
разобьем диск на достаточно узкие кольца шириной ![]() и по
заданному
и по
заданному ![]() вычислим число частиц
вычислим число частиц ![]() , попадающих в
, попадающих в ![]() -е
кольцо. Так, в "стандартной" модели Острайкера и Пиблса [216]
-е
кольцо. Так, в "стандартной" модели Острайкера и Пиблса [216]
![]() и число
и число
![]() , а в модели
экспоненциального диска [
, а в модели
экспоненциального диска [
![]() ] число частиц в кольце
равно
] число частиц в кольце
равно
Каждое кольцо разделим на ![]() равных частей в азимутальном
направлении и в каждую полученную таким образом ячейку поместим
частицу. Координаты частицы внутри ячейки естественно определить с
помощью двукратного применения генератора случайных чисел (один
раз -- в радиальном направлении, второй -- в азимутальном),
сопоставляя интервал изменения случайных чисел (обычно -- [
равных частей в азимутальном
направлении и в каждую полученную таким образом ячейку поместим
частицу. Координаты частицы внутри ячейки естественно определить с
помощью двукратного применения генератора случайных чисел (один
раз -- в радиальном направлении, второй -- в азимутальном),
сопоставляя интервал изменения случайных чисел (обычно -- [![]() ]) с
шириной кольца
]) с
шириной кольца ![]() и шириной сектора
и шириной сектора
![]() . После этого в каждом кольце вычисляем среднюю по
. После этого в каждом кольце вычисляем среднюю по ![]() частицам радиальную гравитационную силу
частицам радиальную гравитационную силу ![]() , действующую на каждую
частицу со стороны всех остальных частиц диска и статического гало (см.
ниже). И всем частицам рассматриваемого кольца придаем азимутальную
скорость
, действующую на каждую
частицу со стороны всех остальных частиц диска и статического гало (см.
ниже). И всем частицам рассматриваемого кольца придаем азимутальную
скорость
![]() . Ясно, что приготовленный таким
образом диск является хотя и равновесным, но "холодным" и, следовательно,
подверженным сильной гравитационной неустойчивости.
. Ясно, что приготовленный таким
образом диск является хотя и равновесным, но "холодным" и, следовательно,
подверженным сильной гравитационной неустойчивости.
Удовлетворительная равновесная модель "горячего" диска
конечной толщины может быть построена на основе шварцшильдовской
функции распределения (2.1.34). Для этого достаточно каким-либо
образом задать распределения двух параметров -- дисперсий скоростей
частиц в радиальном и перпендикулярном плоскости диска
направлениях: ![]() ;
; ![]() . Определение первой из
них естественно делать, используя результаты теории гравитационной
устойчивости звездного диска. Для этого, определив эпициклическую
частоту3.4
. Определение первой из
них естественно делать, используя результаты теории гравитационной
устойчивости звездного диска. Для этого, определив эпициклическую
частоту3.4
![]() на заданном наборе колец, находим
на заданном наборе колец, находим
![]() -- дисперсию радиальных скоростей звезд, необходимую для
подавления неустойчивости осесимметричных возмущений в тонком диске. И затем
задаем величину
-- дисперсию радиальных скоростей звезд, необходимую для
подавления неустойчивости осесимметричных возмущений в тонком диске. И затем
задаем величину
![]() . Значение параметра
. Значение параметра ![]() должно быть, очевидно, обусловлено целями эксперимента. Так, в работах
[217,218]3.5
должно быть, очевидно, обусловлено целями эксперимента. Так, в работах
[217,218]3.5
![]() --
в этом случае величина
--
в этом случае величина ![]() примерно равна
минимально необходимой
примерно равна
минимально необходимой ![]() для подавления гравитационной
неустойчивости в однородном дифференциально вращающемся тонком
диске. Определенная таким образом величина
для подавления гравитационной
неустойчивости в однородном дифференциально вращающемся тонком
диске. Определенная таким образом величина ![]() может оказаться
слишком большой в центральной части диска, где локальные критерии
устойчивости (2.2.41), (2.4.21) не применимы. В этой области удобно принять
может оказаться
слишком большой в центральной части диска, где локальные критерии
устойчивости (2.2.41), (2.4.21) не применимы. В этой области удобно принять
![]() , выбрав
, выбрав
![]() .
.
В соответствии с условием равновесия (2.1.36) азимутальную дисперсию
скоростей полагаем равной
![]() , а
величину дисперсии скоростей частиц поперек плоскости диска
, а
величину дисперсии скоростей частиц поперек плоскости диска
![]() [см. (2.5.18)].
[см. (2.5.18)].
Для моделирования функции распределения (2.1.44) в каждом из трех
![]() направлений исходим из того, что
направлений исходим из того, что
Для каждой частицы генерируем случайное число
находим
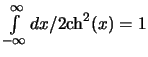 [см. (2.1.45)]
определяем
[см. (2.1.45)]
определяем
В результате выполнения всех этих процедур получаем модель
"горячего" звездного диска конечной толщины, в которой необходимо
еще скорректировать координаты частиц и их скорости таким образом,
чтобы центр масс системы частиц в ходе эксперимента оставался в
начале координат. Кроме того, необходимо еще скорректировать
скорость вращения частиц. Действительно, условие радиального
равновесия горячего диска не сводится к взаимной компенсации
гравитационной и центробежной сил. Его нетрудно получить,
интегрируя с множителем ![]() стационарное осесимметричное
(
стационарное осесимметричное
(
![]() ,
,
![]() ) кинетическое уравнение
(2.1.2) по пространству скоростей:
) кинетическое уравнение
(2.1.2) по пространству скоростей:
2. Гало. При постановке экспериментов, в которых помимо диска
плоской галактики моделируется и ее сферическая подсистема (гало),
необходимо учесть, что дисперсия скоростей звезд гало значительно
превышает дисперсию скоростей звезд диска ([14,98], гл. 1). В то же
время величина возмущений плотности всякой подсистемы обратно
пропорциональна квадрату ее дисперсии скоростей ([197], п. 2.2.2).
Поэтому в процессе эволюции диска, не меняющей существенно
распределение масс в нем, гало можно считать невозмущающимся и
моделировать потенциалом ![]() , действующим на звезды диска. Это
подтвердили и непосредственные численные эксперименты, проведенные
Холом [248], Селвудом [249], в которых моделировались и диск и
гало. Было обнаружено, что гало остается практически статичным.
, действующим на звезды диска. Это
подтвердили и непосредственные численные эксперименты, проведенные
Холом [248], Селвудом [249], в которых моделировались и диск и
гало. Было обнаружено, что гало остается практически статичным.
Потенциал ![]() в свою очередь определяется распределением
плотности вещества
в свою очередь определяется распределением
плотности вещества ![]() в гало. Во многих моделях,
учитывающих постоянство скорости вращения вещества диска на его
периферии [29,30], полагают
в гало. Во многих моделях,
учитывающих постоянство скорости вращения вещества диска на его
периферии [29,30], полагают
![]() . В соответствии с этим
естественна модель гало с распределением объемной плотности
. В соответствии с этим
естественна модель гало с распределением объемной плотности
В описанной выше модели параметр
3. Взаимодействие частиц в диске. Взаимодействие частиц друг
с другом должно, очевидно, моделировать основные свойства
звездного диска как бесстолкновительной гравитирующей системы.
Конструктивное в экспериментальном плане определение
бесстолкновительности диска можно сформулировать следующим
образом: сила, действующая на данную частицу со стороны всех
остальных частиц диска, должна быть заметно больше силы,
действующей на ту же частицу со стороны ее ближайшей соседки. Это
определение естественным образом приводит к необходимости
"обрезания" гравитационного взаимодействия частиц на малых
расстояниях, что использовалось во всех численных экспериментах. Для
оценки величины соответствующего параметра определим "радиус
взаимодействия"
![]() соотношением
соотношением
По данным наблюдений в дисках галактик
Предположим теперь, что "обрезание" гравитационного взаимодействия на малых расстояиях мы осуществляем, вычисляя силу, действующую на
где
Однако описанный выше алгоритм вычисления силы взаимодействия
между частицами при
![]() [216-218,250]
удовлетворителен лишь при изучении коллективных процессов в
плоскости диска. Действительно, при условии сохранения
геометрического подобия экспериментальных моделей реальным
галактикам (
[216-218,250]
удовлетворителен лишь при изучении коллективных процессов в
плоскости диска. Действительно, при условии сохранения
геометрического подобия экспериментальных моделей реальным
галактикам (
![]() ) можно надеяться, что
правильное моделирование коллективных процессов поперек плоскости диска
будет иметь место только в том случае, если
) можно надеяться, что
правильное моделирование коллективных процессов поперек плоскости диска
будет иметь место только в том случае, если
![]() . Поскольку
. Поскольку
![]() , то при
, то при
![]() для выполнения условия
для выполнения условия
![]() необходимо
необходимо
![]() частиц. Следует еще отметить, что в
описанных выше моделях
плоских галактик число частиц обычно невелико. Поэтому полученные в ходе
обработки результатов значения локальных параметров диска испытывают
со временем довольно заметные флуктуации. Однако если целью
эксперимента является изучение характеристик стационарного диска, то влияние
указанных флуктуаций может быть существенно уменьшено, если конечные
результаты получать посредством усреднения по достаточно большому
промежутку времени
частиц. Следует еще отметить, что в
описанных выше моделях
плоских галактик число частиц обычно невелико. Поэтому полученные в ходе
обработки результатов значения локальных параметров диска испытывают
со временем довольно заметные флуктуации. Однако если целью
эксперимента является изучение характеристик стационарного диска, то влияние
указанных флуктуаций может быть существенно уменьшено, если конечные
результаты получать посредством усреднения по достаточно большому
промежутку времени ![]() (порядка времени оборота диска). При таком
подходе число частиц, эффективно участвующих в эксперименте,
достигает величины
(порядка времени оборота диска). При таком
подходе число частиц, эффективно участвующих в эксперименте,
достигает величины ![]() , где
, где
![]() (
(![]() -- величина шага по времени при интегрировании системы уравнений
движения частиц).
-- величина шага по времени при интегрировании системы уравнений
движения частиц).
3.1.3 Модели типа "частица-сетка"
(PM)
В моделях данного типа конфигурационное пространство и, как
правило, пространство скоростей разбиваются на ячейки, в которых и
локализуются частицы. Непосредственно в модели PM
взаимодействие частиц, находящихся внутри одной и той же ячейки
конфигурационного пространства, не учитывается, а взаимодействие частиц,
находящихся в различных ячейках, моделируется ньютоновскими гравитационными
силами, вычисляемыми, как правило, по координатам центров ячеек.
Тем самым осуществляется полное "выключение" гравитационного
взаимодействия на расстояниях, меньших размера ячейки (масштаб
"обрезания" тождественно равен размеру ячейки). Взамен, поскольку
число ячеек ![]() много меньше
много меньше ![]() , имеем выигрыш в скорости расчета,
что позволяет проводить численные эксперименты за приемлемое
машинное время с моделями, содержащими до
, имеем выигрыш в скорости расчета,
что позволяет проводить численные эксперименты за приемлемое
машинное время с моделями, содержащими до
![]() частиц. Модели этого типа подробно описаны в работах [210-213,251-254] и в ряде других.
частиц. Модели этого типа подробно описаны в работах [210-213,251-254] и в ряде других.
Учет взаимодействия между центрами пространственных ячеек при большом числе частиц в каждой ячейке обычно осуществляется с использованием дискретного аналога теоремы о свертке и алгоритма быстрого преобразования Фурье. Принципы учета сферической подсистемы (гало+балдж) и задания начального состояния вполне сходны для методов PP и PM.
Можно построить модели, которые отчасти соединяют в себе
быстроту расчета метода PM и учет близкодействующих
сил, как в моделях PP. Такого рода модели называют
"частица-частица - частица-сетка" (P![]() M) и в основе их лежит
расщепление действующих между частицами сил на две части: быстро меняющуюся
короткодействующую часть и медленно меняющуюся дальнодействующую [241].
M) и в основе их лежит
расщепление действующих между частицами сил на две части: быстро меняющуюся
короткодействующую часть и медленно меняющуюся дальнодействующую [241].
Естественно, от построенных моделей необходимо требовать выполнения законов сохранения энергии и момента импульса. На практике обычно достигают точности сохранения этих величин порядка нескольких процентов.
Метод PP с использованием временного усреднения вполне пригоден для изучения глобальной квазистационарной структуры галактик. Для исследования эволюционных процессов более приемлемым является метод PM.
3.1.4 Иерархические модели (TREE-модели)
Данный подход к численному решению гравитационной задачи ![]() тел предложен не так давно [255,256]. В основе метода лежит
формирование древовидной (TREE) иерархической системы сеток.
Система таких сеток располагается в порядке подробности от
наиболее мелких, где учитываются наиболее близкодействующие силы,
которые учитываются достаточно точно, ко все более грубым, на
которых учитываются дальнодействующие силы. Другими словами,
производится регуляризация как двойных сближений, так и сближений
подсистем на разных уровнях иерархии. Алгоритм требует порядка
тел предложен не так давно [255,256]. В основе метода лежит
формирование древовидной (TREE) иерархической системы сеток.
Система таких сеток располагается в порядке подробности от
наиболее мелких, где учитываются наиболее близкодействующие силы,
которые учитываются достаточно точно, ко все более грубым, на
которых учитываются дальнодействующие силы. Другими словами,
производится регуляризация как двойных сближений, так и сближений
подсистем на разных уровнях иерархии. Алгоритм требует порядка
![]() вычислений на каждом шаге интегрирования.
вычислений на каждом шаге интегрирования.
Достаточно детальное описание метода с некоторыми модификациями дано Джернигамом и Портером [257]. Сравнение с известными модельными результатами показало хорошее соответствие, а также подтвердило преимущества, связанные с затратами машинного времени. TREE-модели позволяют изучать сложные системы, включающие три взаимодействующие компоненты: звездный и газовый диски, "живое" гало [258,259].
Введение в практику иерархических схем фактически подводит
нас к естественному пределу в построении численных методов [260]. В
последние годы развитие пошло по пути создания специализированных
компьютеров для численного решения гравитационной задачи ![]() тел, в
которых вычисление взаимодействия между телами реализовано
аппаратно [261]. Непосредственное моделирование на такого рода
компьютерах говорит об их больших возможностях [262].
тел, в
которых вычисление взаимодействия между телами реализовано
аппаратно [261]. Непосредственное моделирование на такого рода
компьютерах говорит об их больших возможностях [262].
Сравнительный обзор различныых методов численного
моделирования ![]() гравитирующих тел можно найти, например, в [241,263,264].
гравитирующих тел можно найти, например, в [241,263,264].
<< 3. Моделирование звездных дисков | Оглавление | 3.2 Крупномасштабная структура ... >>
|
Публикации с ключевыми словами:
аккреционный диск - диск, галактический - гидродинамика - спиральная структура
Публикации со словами: аккреционный диск - диск, галактический - гидродинамика - спиральная структура | |
См. также:
Все публикации на ту же тему >> | |