§ 7.3 Волны плотности во вращающихся галактиках
В этой главе мы рассматриваем гравитирующие звездные системы, состоящие из несталкивающихся между собой материальных точек - звезд. Но для того чтобы пояснить, что такое волны плотности в звездных системах, удобнее начать с системы, состоящей из гравитирующего газа.
Напомним известное дисперсионное соотношение для звуковых волн:
|
|
(7.37) |
где ω - частота волны, vs - скорость звука, λ - длина волны, k - волновое число. Звуковая волна состоит из разрежений и уплотнений газа. Колебания газа в волне определяются тем, что упругая сила единицы объема, равная, по определению, величине ρgω2x, где x - смещение частиц, ρg - средняя плотность газа, создает избыток силы газового давления в уплотнениях волны. Этот избыток пропорционален величине p (x / λ2), где p ∼ ρgT ∼ρgvs2 - среднее давление. Формула (7.37) справедлива лишь в случае звука с малой длиной волны. Если перейти к волнам большей длины, то следует учитывать эффекты самогравитации. В области сжатия газ уплотняется, что приводит к появлению дополнительной силы взаимного гравитационного притяжения, препятствующей последующему расширению. Это в свою очередь эквивалентно появлению "отрицательного" давления в волне. Величину соответствующего вклада в упругую силу можно получить, составив из параметров, характеризующих эффект самогравитации, т. е. величин G, ρ и λ, величину с размерностью ρgω2. Нетрудно убедиться, что такой комбинацией есть произведение G ρg2. Добавляя сюда следующий из точной теории множитель 4π, получим дисперсионное соотношение, определяющее частоту волн "тяжелого звука", т. е. звуковых волн с учетом самогравитации
|
|
(7.38) |
Из этой формулы было получено много следствий. Например, отсюда следует известный критерий неустойчивости Джинса. У волн "тяжелого звука" с большой длиной "отрицательное давление" самогравитации больше обычного газового давления, т. е. vs2k2 < 4 πG ρg. В этом случае флуктуации плотности в волне оказываются неустойчивыми и будут неограниченно сжиматься (что соответствует условию ω2 < 0). Длина волны неустойчивых по Джинсу возмущений
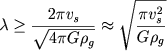
|
(7.39) |
Соответственно для масс флуктуации, на которые распадается неоднородная среда, имеем
|
|
(7.40) |
К вопросу о следствиях неустойчивости Джинса мы вернемся в гл. 8. Здесь же заметим, что формула (7.40) может быть сразу получена из соображений анализа размерностей, поскольку неустойчивость среды по отношению к распаду на флуктуации массой М должна определяться всего четырьмя размервостными определяющими параметрами, входящими в формулу (7.40).
А теперь перейдем .к однородной системе, состоящей из звезд. Здесь тоже могли бы возникать волны плотности, но нет эквивалента газового давления. Поэтому для волн плотности в однородной системе, состоящей из звезд, можно было бы применить соотношение (7.38) при vs = 0. Но это приведет к неустойчивости всех волн плотности, а следовательно, и к неустойчивости звездной системы вообще. Однако есть две причины, снимающие эту неустойчивость и образующие волны плотности в звездных системах.
Во-первых, роль упругости газового давления принимает на себя вращение звездной системы как целого. Для пояснения этого эффекта будем рассуждать так, как это делается при анализе устойчивости вращательного движения жидкости (см. [10]). Пусть звезды движутся во вращающейся звездной системе по приближенно круговым орбитам. Волны плотности, возникающие в такой системе, смещают их со своих орбит. Пусть смещение звезды относительно равновесной орбиты есть δr. На равновесной орбите центробежное ускорение v2 / r = r Ω2(r) компенсировалось силой притяжения этой же звезды со стороны всей звездной системы. После смещения изменится и центробежная сила, действующая на эту звезду. Легко убедиться в том, что возникнет упругая сила, возвращающая звезду обратно на равновесную орбиту, если ее центробежная сила на новой орбите меньше, чем центробежная сила на равновесных орбитах на том же расстоянии.
Чтобы этот эффект выразить математически, запишем величину центробежной силы, действующей на звезду, через сохраняющуюся при смещениях величину момента импульса:
|
|
(7.41) |
Отсюда для центробежной силы имеем
|
|
(7.42) |
После смещения на новой орбите центробежная сила равна ![]() . Но центробежная сила на расстоянии r + δ r от центра вращения есть
. Но центробежная сила на расстоянии r + δ r от центра вращения есть
|
|
(7.43) |
Условие устойчивости звезды на орбите есть FR < FR′ или
|
|
(7.44) |
Еще удобнее это неравенство записать в виде
|
|
(7.45) |
Параметр χ(r) называется эпициклической частотой, поскольку смещение звезд с круговых орбит называют эпициклами.
Элицикличность движения звезд во вращающихся звездных системах и есть та упругая сила, которая делает возможным существование волн плотности, поскольку оно играет роль давления. Вместо уравнения (7.38) теперь получаем
|
|
(7.46) |
где ρ* - плотность распределения звезд. Правда, из (7.46) на первый взгляд следует, что волн плотности здесь, собственно говоря, нет, поскольку в правой части этого соотношения нет длины волны. Иными словами, (7.46) определяет только некоторую характерную частоту колебаний концентрации звезд. На самом деле зависимость частоты а от длины волны здесь есть.
Дело в том, что эффект самогравитации волн плотности существенно зависит от дисперсий скоростей звезд. Очевидно, что если пекулярные скорости звезд велики, то звезды быстро убегают из области сжатия, в волне плотности и поэтому эффект самогравитации волн плотности не успевает проявиться. Критерием является сравнение пекулярных скоростей звезд, обозначаемых через vI, с фазовой скоростью волн плотности ω / k. Заменяя здесь ω на χ, получим неравенство, при котором волны плотности существуют:
|
|
(7.47) |
Более строгое рассмотрение позволяет записать дисперсионное соотношение (7.46) в виде
|
|
(7.48) |
где ρ* - по-прежнему звездная плотность, а фактор редукции f быстро спадает с ростом аргумента. При не слишком больших значениях этой величины имеем f ∼ exp(-(vIk / χ)2). Таким образом, во вращающейся звездной системе также имеются волны плотности, устойчивые при малых длинах волн (больших k), если только дисперсия пекулярных скоростей звезд не слишком мала. Волны с большой длиной могут быть неустойчивыми (типа неустойчивости Джинса), но здесь все волны плотности могут быть устойчивыми, если только эпициклическая частота достаточно велика, точнее, если
|
|
(7.49) |
До сих пор мы не учитывали, что вращающиеся звездные системы, как правило, имеют геометрию плоского диска. В этом случае приведенные выше соотношения справедливы только до тех пор, пока длина волны плотности много меньше толщины плоского диска галактики. Если же рассматриваются волны плотности с длиной волны, много большей толщины слоя, то во всех приведенных соотношениях следует величину ρ*. заменить на (1/2)ρSk = (π ρS) / λ, где ρS - поверхностная плотность звезд, а k - горизонтальное (т. е. расположенное в плоскости диска) волновое число.
Дисперсионное соотношение для концентрических воля плотности во вращающемся диске галактики записывается в виде
|
|
(7.50) |
где фактор f описывается сложной функцией с асимптотическими выражениями:
|
|
(7.51) |
|
|
Волны плотности, описываемые этими выражениями, состоят из концентрических колец разрежений и сжатий газа по всему сечению диска, распространяющихся от центра галактики, если k > 0, и стягивающихся к центру при k < 0.
Из формулы (7.50) вытекает условие устойчивости звездного диска по отношению к волнам плотности (см. [11]). В самом деле, для устойчивости диска необходимо, чтобы для всех возможных волн (т. е. для любых k] частота волн плотности была бы действительной, т. е. ω2 > 0. Отсюда условие устойчивости
|
|
(7.52) |
Если для фактора f принять первую формулу (7.51), то условие (7.52) эквивалентно неравенству'
|
|
(7.53) |
Более точный расчет, учитывающий точное выражение функции f, дает численный .множитель, равный 0,34. Таким образом, звездный диск может существовать только в том случае, если дисперсия скоростей звезд больше определенного предела, который здесь играет роль скорости звука в неустойчивости Джинса. Если критерий (7.53) не выполнен, то вращающийся звездный диск распадается на отдельные сгущения.
Если подставить vI из (7.53) в определение времени релаксации однородного звездного диска ((7.34) при ![]() ), то получим:
), то получим:
|
|
(7.54) |
где также принято χ ∼ Ω.
Однако основное значение волн плотности в звездном диске заключается в том, что при их помощи можно объяснить спиральную структуру галактик - в этом заключается основная идея теории спиральной структуры Лина - Шу (см. [12-15]). Формула (7.50) описывает волны плотности в виде концентрических кругов, а дисперсионное соотношение
|
|
(7.55) |
описывает также волны плотности, но имеющие форму спиралей, закручивающихся при k < 0 и раскручивающихся при k > 0. Здесь m - целое число, определяющее количество cпиральных рукавов.
Вся спиральная структура вращается с угловой скоростью
|
|
(7.56) |
где ω определяется уравнением (7.55). Обычно в галактиках имеется два спиральных рукава, т. е. m=2. Расстояние между соседними витками спирали равно λ / m. Спиральная структура занимает ие весь вращающийся диск, а только полосу, в которой выполнено условие
|
|
(7.57) |
Чем больше число рукавов, тем уже занимаемая имя область.
Спиральные волны плотности не только вращаются с определенной угловой скоростью, но также и перемещаются вдоль радиуса с групповой скоростью [16]
|
|
(7.58) |
Это приводит к тому, что спиральные волны плотности все время стягиваются к центру галактики и требуется их постоянная "подкачка" для сохранения всей спиральной картины в течение достаточно долгого промежутка времени.
Сопоставление наблюдений и теории (см. [13, 14]) дает в общем согласованную картину, объясняющую реальную структуру нашей Галактики и нескольких соседних галактик. Много проблем теории спиральной структуры остается нерешенными, из них наиболее трудная - проблема возбуждения спиральных волн плотности. В связи с этим большое внимание уделялось численному моделированию звездных систем. Этому вопросу будет посвящен раздел 5.
<< § 7.2 Время релаксации звездных систем | Оглавление | § 7.4 Численное моделирование эволюции звездных скоплений >>