§ 7.2 Время релаксации звездных систем
Важнейшей проблемой динамики звездных -систем является определение ее характерного времени релаксация, которую мы будем обозначать через tE. Это определение связано с различием между регулярными и иррегулярными силами в звездных системах. Общая теория излагалась во многих работах и книгах (см., например, [3]). Здесь мы ограничимся лишь простой трактовкой, основанной ла теории анализа размерностей и качественных соображениях
Силы, действующие на движение звезд в звездных системах, можно разделить на два типа. Регулярные силы возникают от действия общего, так называемого самосогласованного, гравитационного поля всей системы. Под действием этой силы звезда описывает в системе некоторую более или менее правильную орбиту. Например, во вращающейся спиральной галактике звезды описывают почти круговые орбиты под действием регулярного гравитационного поля. В квазисферичеоких звездных системах тоже имеются регулярные орбиты, но они могут быть существенно более эллиптичными. Характерный период движения звезд под действием регулярных сил называется временем пересечения P в скоплениях или периодом обращения 2π / Ω во вращающихся галактиках. Содержание предыдущего параграфа есть, по существу, определение характерного времени регулярных сил.
Регулярные силы определяют характерную величину регулярных скоростей, примерно равную vR ≈ R/P или vR = RΩ для скоплений или вращающихся галактик соответственно. Поэтому можно написать
|
|
(7.18) |
если воспльзоваться определениями (7.8) и (7.9). Можно определить и величину безразмерного комплекса Π, если воспользоваться теоремой вириала или какими-нибудь другими соображениями. Например, для строго вращательного движения сила гравитационного притяжения на краю системы ![]() должна равняться ценробежной силе vR2 / R. Здесь Π = 1. Однако из теоремы вириала параметр Π имеет большее значение, строго говоря зависящее от геометрии системы. Для однородных сферических систем гравитационная потенциальная энергия
должна равняться ценробежной силе vR2 / R. Здесь Π = 1. Однако из теоремы вириала параметр Π имеет большее значение, строго говоря зависящее от геометрии системы. Для однородных сферических систем гравитационная потенциальная энергия
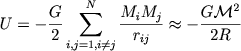
|
(7.19) |
и кинетическая энергия
|
|
(7.20) |
Из теоремы вириала следует, что &Pi = 2, т.е
|
|
(7.21) |
Этим соотношением мы и будем пользоваться
Теперь перейдем к анализу иррегулярных сил ,и скоростей. Они связаны со сближениями отдельных звезд, при которых скорости этих звезд испытывают значительные изменения. Изменение скорости при сближениях имеет стохастический характер и поэтому заметен лишь суммарный эффект многих сближений. Действие иррегулярных сил описывается характерным временем релаксации tE, т. е. промежутком времени, в течение которого заметно изменится скорость звезды под действием стохастических сближений, либо соответствующей длиной свободного пробега, обозначаемой в дальнейшем через lE.
Элементарное определение lE можно получить следующим образом. Очевидно, что эта величина равна
|
|
(7.22) |
где ![]() , по-прежнему, концентрация звезд, π s2 - эффективное сечение звездных сближений, Λ - кулоновский логарифм, учитывающий вклад далеких сближений. Для определения параметра s - прицельного расстояния сближения - поступим следующим образом. Будем считать сближение эффективным, если при этом скорость возрастет не менее, чем на некоторую заданную величину vi. Приравнивая приращение кинетической энергии звезды со средней массой
, по-прежнему, концентрация звезд, π s2 - эффективное сечение звездных сближений, Λ - кулоновский логарифм, учитывающий вклад далеких сближений. Для определения параметра s - прицельного расстояния сближения - поступим следующим образом. Будем считать сближение эффективным, если при этом скорость возрастет не менее, чем на некоторую заданную величину vi. Приравнивая приращение кинетической энергии звезды со средней массой ![]() потенциальной энергии сближения на прицельном расстоянии GM2 / s получим
потенциальной энергии сближения на прицельном расстоянии GM2 / s получим
|
|
(7.23) |
Подставляя в (7.22) также ![]() и учитывая (7.21), где
и учитывая (7.21), где ![]() , получим
, получим
|
|
(7.24) |
В квазисферических невращающихся системах иррегулярные силы оказывают заметное действие тогда, когда скорости vi оказываются сравнимыми с vR. Кроме того, как показывает расчет, в таких системах с большим числом частиц кулоновский логарифм в первом приближении равен Λ = ln N [3]. Таким образом,
|
|
(7.25) |
Численноый коэффициент 1 / 12 несколько изменяется при более рафинированном расчете.
В плоских вращающихся галактиках эффект иррегулярных сил приводит к меньшему изменению скоростей, чем величина vR, которая здесь соответствует линейной скорости вращения. Под vI, тут следует понимать дисперсию пекулярных скоростей звезд. Наблюдательные данные показывают, что в быстро вращающихся плоских галактиках отношение vI / vR очень мало, вероятно, меньше 1/10. Поэтому для спиральных галактик отношение lE / R должно быть порядка 10-5 N / ln N. Но эта величина все же на много порядков больше единицы, так как N ≈ 1010 - 1012 .
Величина длины свободного пробега заметно уменьшается при учете неоднородности звездной системы. Это можно увидеть сразу же из формул (7.22) и (7.23). Допустим, что в звездной системе есть большие флуктуации плотности числа звезд, т. е. система неоднородна. Пусть масса каждой флуктуации порядка Mф (Mф » ![]() ) и примем, что число таких флуктуации на единицу объема есть nф. Для оценки длины свободного пробега также можно использовать формулу (7.23), заменив в ней
) и примем, что число таких флуктуации на единицу объема есть nф. Для оценки длины свободного пробега также можно использовать формулу (7.23), заменив в ней ![]() на Mф. В результате получим для длины свободного пробега
на Mф. В результате получим для длины свободного пробега
|
|
(7.26) |
Здесь принято, что средняя плотность массы во флуктуациях, т. е. величина nфMф, не слишком сильно отличается от средней плотности звезд вообще, т. е. от величины ![]() . Кроме того, при рассеянии звезд на больших флуктуациях кулоновекий логарифм Λ порядка единицы. Из (7.26) сразу видно, что в неоднородной системе, в которой звезды распределены в виде совокупности звездных облаков, каждое из которых содержит очень большое число звезд (Mф »
. Кроме того, при рассеянии звезд на больших флуктуациях кулоновекий логарифм Λ порядка единицы. Из (7.26) сразу видно, что в неоднородной системе, в которой звезды распределены в виде совокупности звездных облаков, каждое из которых содержит очень большое число звезд (Mф » ![]() ), длина свободного пробега уменьшается очень сильно. Если бы вся галактика состояла яз звездных скоплений с массой порядка 105 маос Солнца, то можно было бы получить длину свободного пробега, сравнимую с ее размером. Однако на самом деле звездный фон в галактиках существенно однороднее и здесь всегда lE » R.
), длина свободного пробега уменьшается очень сильно. Если бы вся галактика состояла яз звездных скоплений с массой порядка 105 маос Солнца, то можно было бы получить длину свободного пробега, сравнимую с ее размером. Однако на самом деле звездный фон в галактиках существенно однороднее и здесь всегда lE » R.
При численном моделировании часто рассматривают идеально плоскую систему; считается, что все звезды движутся в одной плоскости. Поэтому соотношение между длиной свободного пробега и R оказывается существенно другим [4]. Вместо (7.22) имеем
|
|
(7.27) |
поскольку эффективное сечение взаимодействия представляет собой отрезок в плоскости движения, равный 2s, где s по-прежнему, прицельное расстояние. Полагая ![]() и учитывая (7.23) и (7.21), получим
и учитывая (7.23) и (7.21), получим
|
|
(7.28) |
Здесь lE « R, даже если vI сравнимо с vR- Определение (7.28) для длины свободного пробега применимо и к физически реальным системам, если параметр s из (7.23) сравним или меньше толщины системы (здесь vI - дисперсия скоростей в плоскости движения).
Характерное время релаксации определяется как отношение длины свободного пробега к средней скорости движения звезд. Однако мы определим эту величину другим способом, используя соображения анализа размерностей. Это сделано в книге [5], но мы воспользуемся другим методом.
Прежде всего выделим основные определяющие параметры. Иррегулярные силы, приводящие к релаксации системы, зависят от постоянной G, маос отдельных звезд, т. е. ![]() , концентрации звезд
, концентрации звезд ![]() и некоторой средней скорости частиц, которую мы пока обозначим через v ′. Искомая величина tE имеет размерность времени. Из этих определяющих параметров составим матрицу размерности
и некоторой средней скорости частиц, которую мы пока обозначим через v ′. Искомая величина tE имеет размерность времени. Из этих определяющих параметров составим матрицу размерности
![$$
\begin{matrix}
\, & [G] & [\overline{M}] & [\overline{n}] & [v^{\prime}] & [t_{E}] \\
\mbox{г} & -1 & 1 & 0 & 0 & 0 \\
\mbox{см} & 3 & 0 & -3 & 1 & 0 \\
\mbox{сек}&-2 & 0 & 0 & -1 &1
\end{matrix}
$$](http://images.astronet.ru/pubd/2013/03/01/0001281314/tex/formula780.gif)
|
Ранг матрицы равен трем, т. е. есть два независимых безразмерных комплекса. Можно их выбрать произвольным образом, используя те или иные физические соображения. Во-первых, составим эти комплексы так, чтобы tE входило бы в них в первой степени. Во-вторых, один из комплексов составим без скорости v ′. Тогда получим
|
|
(7.29) |
Во втором комплексе оставим все определяющие параметры, но потребуем, чтобы величина tE была бы обратно пропорциональна концентрации звезд, иными слoвами, в этот комплекс входило бы произведение ![]() . Тогда имеем
. Тогда имеем
|
|
(7.30) |
В таком определении может заключаться некоторый произвол, но, как мы увидим ниже, этот выбор действительно оправдан. Сопоставим безразмерный комплекс (7.29) с соотношением (7.13). Отсюда сразу следует, что если tE порядка времени пересечения P, то Π1 - порядка единицы. Но мы уже знаем, что у систем с большим числом звезд длина свободного пробега много больше характерных размеров и, следовательно, время релаксации должно быть много больше времени пересечения. Поэтому в таких системах Π1 » 1, и этот безразмерный комплекс не может характеризовать определение времени релаксации.
Остается безразмерный комплекс (7.30), откуда следует
|
|
(7.31) |
где Π2 не может очень сильно отличаться от единицы. Как уже отмечалось, здесь есть некоторый произвол, связанный с тем, что мы считали ![]() . Но это очевидно, так как чем больше концентрация звезд, тем меньше и время релаксации. Кроме того, здесь учтено, что релаксация происходит при взаимодействии отдельных звезд, т. е. как бы при их "столкновениях". Частота столкновений всегда обратно пропорциональна концентрации.
. Но это очевидно, так как чем больше концентрация звезд, тем меньше и время релаксации. Кроме того, здесь учтено, что релаксация происходит при взаимодействии отдельных звезд, т. е. как бы при их "столкновениях". Частота столкновений всегда обратно пропорциональна концентрации.
Сопоставляя (7.31) с (7.24) и (7.25), а также учитывая определение времени пересечения (7.13), можно получить соотношение
|
|
(7.32) |
при соответствующем выборе численного значения безразмерного комплекса Π2 (пропорционального (ln N)-1) и условии v ′ = vR из (7.21). Это соотношение мы и примем за определение характерного времени релаксации для квазисферических невращающихся скоплений.
Характерное время релаксации в плоских спиральных галактиках связано с длиной свободного пробега (7.26) подобным соотношением, если считать скорость v ′ в (7.31) равной скорости vI в (7.24). Вместо времени пересечения здесь следует учесть период обращения. Получаем следующую формулу, учитывающую также наличие флуктуации массы:
|
|
(7.33) |
Здесь под vI, следует понимать пекулярную скорость звезд, а vR, есть линейная скорость вращения галактики. Если сюда подставить vR ≈ R Ω , а вместо N ввести среднюю поверхностную концентрацию звезд ![]() , то получим следующее соотношение
, то получим следующее соотношение
|
|
(7.34) |
Эту формулу можно применять для оценки релаксации звезд разного типа в галактиках.
Резюмируя все сказанное о времени релаксации звездных систем, можно сделать следующий общий вывод. В квазисферических невращающихся звездных скоплениях, состоящих из сотен (до тысячи) звезд, характерное время релаксации сравнимо со временем пересечения звездой диаметра скопления. Такие системы быстро релаксируют и все время находятся в квазиравнозесном состоянии. Квазисферические невращающиеся системы, состоящие из сотен тысяч звезд (шаровые скопления), имеют большое время релаксации, много большее, чем время пересечения. Впрочем, за достаточно большой промежуток времени и эти системы успевают достигнуть квазиравновесного состояния.
В спиральных плоских галактиках, состоящих из сотен миллиардов звезд, время релаксации при сближениях отдельных звезд очень велико и не может привести к заметному перераспределению скоростей звезд. Здесь нет поэтому и квазиравновесного состояния всей системы. Однако определенное перераспределение энергии все же имеет место благодаря коллективным процессам в таких системах.
Эволюция квазисферических невращающихся скоплений с N ≈ 102-105 и плоских спиральных галактик с N ≈ 1010-1012 принципиально различна. В скоплениях эволюция приводит к вылету звезд из скопления, а в плоских вращающихся галактиках эволюция связана с возникновением волн плотности - спиральных рукавов.
Проблеме вылета звезд из скопления было посвящено много работ, начиная с первой работы В. А. Амбарцумяяа [6] (см. также [3]).
В наиболее простой постановке задача расчета скорости вылета звезд из скопления выглядит следующим образом. Допустим, что за время, равное времени релаксации tE, в звездной системе устанавливается максвелловское распределение скоростей со средней характерной скоростью (7.21). При этом некоторая часть звезд приобретает скорость, большую параболической:
|
|
(7.35) |
Если считать, что при v > v∞ распределение скоростей максвелловское, то относительное число звезд со скоростями, большими параболической равно [6]
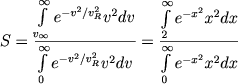
|
(7.36) |
Звезды со скоростями, большими параболической, покидают скопление и поэтому можно считать, что за время одной релаксации скопление теряет 0,74% от полного числа звезд.
Более подробный анализ должен учитывать, что характерное время релаксации различно для звезд разной массы, и поэтому скопление теряет по-разному легкие и тяжелые звезды. Чандраcекаром [3] было показано, что если предположить, что звезды разной массы распределены равномерно по объему скопления, то в первую очередь вылетают звезды с массой около ![]() , причем за среднее время релаксации вылетают 3-4% от полного числа таких звезд. Звезды с массой около
, причем за среднее время релаксации вылетают 3-4% от полного числа таких звезд. Звезды с массой около ![]() вылетают с такой же скоростью, что и звезды со средней массой
вылетают с такой же скоростью, что и звезды со средней массой ![]() , т. е. их вылетает 0,74% за одно среднее время релаксации. С другой стороны, звезды очень малых (
, т. е. их вылетает 0,74% за одно среднее время релаксации. С другой стороны, звезды очень малых (![]() ) или больших (
) или больших (![]() ) масс вылетают .медленно - за одно время релаксации теряется 0,1-0,2% от полного числа таких звезд.
) масс вылетают .медленно - за одно время релаксации теряется 0,1-0,2% от полного числа таких звезд.
Впрочем, предположение о равномерности распределения звезд по объему скопления или хотя бы о подобности такого распределения для звезд разных масс, вероятно, далеко от реальности. Звезды больших масс должны концентрироваться к центральной части скопления, а легкие звезды чаще встречаются на периферии. В результате скорости потерь звезд разной массы выравниваются. Оценки этого явления, сделанные разными авторами [7, 8, 9], расходятся и поэтому для простоты можно ограничиться первым условием - скопление теряет 0,7-0,8% от полного числа звезд за одно время релаксации.
Поскольку вылетающие звезды уносят с собой положительную энергию, то абсолютное значение отрицательной полной энергии скопления все время растет (примерно на 0,52% за время релаксации) и скопление становится со временем плотнее и компактнее. Возможно, что при этом происходит некоторое обогащение скопления тяжелыми звездами.
<< § 7.1 Система уравнений и параметры звездных систе | Оглавление | § 7.3 Волны плотности во вращающихся галактиках >>