§ 5.3 Турбулентность и конвекция
В физике звезд большую роль играет явление конвекции. Мы уже видели в предыдущей главе, что конвективный перенос энергии существен как в горячих звездах (конвективные ядра), так и в холодных (конвективные зоны вблизи поверхности). Конвективные движения вблизи поверхности звезд генерируют звуковые волны, нагревающие самые верхние слои атмосферы. Таким образом создаются хромосфера и корона Солнца и, по существу, конвекция находится в основе всего многообразия солнечных явлений.
К сожалению, явление звездной конвекции еще далеко от более или менее полного теоретического объяснения. Дело в том, что звездная конвекция в основном имеет турбулентный характер, а теория развита преимущественно для случая ламинарной конвекции. Тем не менее удалось получить много интересных результатов. Как в теории турбулентности, так и в теории конвекции методы анализа размерностей и теория подобия играют очень большую роль. Поэтому кажется уместным дать изложение тех результатов теории конвекции и турбулентности, которые были получены методом анализа размерностей или теории подобия и которые могут найти или уже нашли себе применение в физике звезд и межзвездной среды. Сначала рассмотрим закономерности турбулентности в общем виде, не специализируя причин, которые ее вызывают.
Как известно, турбулентностью называется такое состояние среды, при котором возбуждены движения разных масштабов, причем имеет место перекачка энергии между этими движениями. В основе явления турбулентности лежит стремление энергии перераспределиться по большому числу степеней свободы. Допустим, что в некоторой среде было возбуждено движение вещества большого масштаба. Если нет взаимодействия с движениями других масштабов, то энергия этих крупномасштабных движений затухает из-за диссипативных процессов, сохраняя свой характерный масштаб. Но если движения нелинейные, то энергия от движений крупных масштабов переходит к движениям меньших масштабов, где она и диссипирует в тепловую энергию.
Различают два вида турбулентности - вихревую и акустическую. В вихревой турбулентности, как показывает само название, движение вещества имеет характер вихрей различного масштаба. Иными словами, в движениях всех масштабов
|
|
(5.82) |
Можно ввести характерный размер вихря l (его диаметр!) и соответствующую скорость вихревого движения vl. Часто вместо масштаба l вводят понятие о волновом числе вихря k, которое определяется так:
|
|
(5.83) |
В акустической турбулентности движения имеют характер волн, т. е. это движения потенциального типа. В строго акустической турбулентности
|
|
(5.84) |
Движение вещества характеризуется длиной волн или волновыми числами, скоростью распространения этих волн, которую мы будем обозначать через vs, а также скоростью движения вещества, которую будем обозначать через vk. Если волны имеют линейный характер (обычно при vk≪vs), то взаимодействие между волнами разных масштабов несущественно и акустической турбулентности не возникает. Однако при большой амплитуде волн (vk не слишком мало по сравнению со скоростью звука) взаимодействие между волнами разных масштабов оказывается существенным и энергия перекачивается от волн одних масштабов к волнам с другими масштабами.
Основной характеристикой турбулентности является се спектральная функция - распределение энергии по различным масштабам движения или, что одно и то же, зависимость скорости движения от масштаба. Именно для определения этих зависимостей и можно использовать метод анализа размерностей.
В вихревой турбулентности имеет место хорошо известный спектр Колмогорова. Строго говоря, этот спектр получен для частного случая изотропной и однородной турбулентности несжимаемой жидкости. Но многочисленные эксперименты показали его универсальность и применимость к условиям, весьма далеким, от однородности и изотропности.
Спектр Колмогорова основан на предположении, что перекачка энергии между вихрями различных масштабов определяется только одним параметром ε - потоком энергии через всю иерархию вихрей, от самых больших к самым малым. Если считать, что энергия крупномасштабных движений не диссипирует непосредственно в тепло, то величина энергии, передаваемая от вихрей этого масштаба к вихрям меньшего масштаба, постоянна, т. е. не зависит ни от масштаба движений, ни от соответствующих скоростей. Размерность потока энергии, отнесенная к единице массы, есть
|
|
(5.85) |
Предположим, что движение в некоторых масштабах l не зависит от других параметров, кроме ε . Тогда зависимость vl от l может быть получена путем составления безразмерного комплекса из величин ε , l и vl. Учитывая (5.85), сразу получаем с точностью до численного множителя:
|
|
(5.86) |
Определим спектральную функцию энергии турбулентного движения Wk таким образом, чтобы энергия, заключенная в движениях с волновыми числами в интервале от k до k + dk, равнялась Wkdk. Тогда из (5.86) следует
|
|
(5.87) |
где ρ - плотность среды. Соотношения (5.86) и (5.87) и есть спектр Колмогорова.
Спектр Колмогорова нельзя применять непосредственно к движениям самых больших масштабов - здесь ε уже не является единственным определяющим параметром. В частности, скорости движения в этих масштабах зависят и от геометрии среды и от той причины, которая вызывает движения в самых крупных масштабах. Со стороны малых масштабов спектр Колмогорова ограничен влиянием вязкости или других диссипативных процессов. Пусть ν - кинематический коэффициент вязкости или другого диссипативного процесса, который может влиять на характер движения. Его размерность
|
|
(5.88) |
Тогда нижняя граница колмогоровского спектра lν определяется совместным действием ε и ν. Составляя безразмерную комбинацию из этих величин и масштаба lν, получим
|
|
(5.89) |
Реальная вихревая турбулентность в космических условиях, конечно, не является ни изотропной, ни однородной, и имеет место в сжимаемом, газе. Тем не менее псе эти соотношения, имеющие размерностный характер, остаются справедливыми.
Приведем несколько конкретных примеров. На рис. 20 приведена величина энергии движения межзвездной среды W(l) как функция масштаба движения l. Из (5.87) следует соотношение
|
|
справедливое для не слишком больших масштабов.
Наблюдаемая зависимость оказалась несколько более крутой, W(l) ∼ l0,7, [14], но близкой к теоретическому спектру Колмогорова, хотя, конечно, движения межзвездного газа не являются ни изотропными, ни однородными. Величина l0 ≈ 80 - 100 пс характеризует масштаб движений с максимальной плотностью энергии. Далее с ростом l плотность энергии быстро спадает.
Подобные спектры были получены и для движений в туманности Ориона [15]. Вообще различные исследования поведения скоростей в турбулентных астрофизических средах показывают, что по крайней мере не в очень крупных масштабах движений имеет место спектр Колмогорова. К сожалению, построение спектров движений газа в космических объектах часто затруднено тем, что одновременные определения из наблюдений скоростей движения различных масштабов очень сложны.
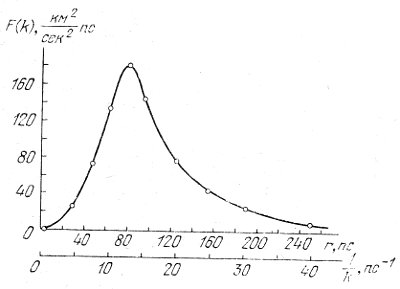
Рис. 20. Спектральная функция межзвездной турбулентности.
Спектру Колмогорова соответствует восходящая часть кривой (до 80 пс).
Размерностное соотношение (5.86) оказывается очень полезным и для оценки диссипации энергии в турбулентных движениях в тех случаях, когда можно определить по данным наблюдений скорость движений и масштаб. Для турбулентности межзвездной среды имеем v = 7 км ⋅ сек-1 и l ≈ 100 пс ≈ 3 ⋅ 1020 см, откуда получаем ε = 10-3 эрг ⋅ г-1 ⋅ сек-1. Такое количество энергии должно поставляться источниками, возбуждающими межзвездную турбулентность.
В качестве другого примера оценим характерные величины крупномасштабных движений в звездной атмосфере, возникающих из-за турбулентной конвекции. Характерный размер наиболее крупномасштабного вихря не может заметно превышать эквивалентную высоту слоя - в противном, случае в одном и том же масштабе движения происходило бы очень сильное изменение плотности. Поэтому
|
|
(5.90) |
где Т - температура слоя и g - ускорение силы тяжести. Скорость движений v0 определяется потоком кинетической энергии, которую эти движения должны переносить, т. е. величиной
|
|
(5.91) |
Здесь считается, что в области конвекции заметная часть полного потока энергии L/4πR2 переносится газодинамическими движениями, скорости которых v0, а плотности энергии ρv02 (ниже будет приведена формула (5.154) для потока тепловой энергии, переносимой конвекцией). Подставляя l0 из (5.90) и v0 из (5.91) в соотношение (5.86), определим диссипацию энергии в слоях звезды с существенным конвективным переносом энергии:
|
|
(5.92) |
где p - давление газа в конвективной зоне. На Солнце величина ε порядка 1012 см2 ⋅ сек-3, у сверхгигантов много меньше, порядка 106 см2 ⋅ сек-3. Но у вспыхивающих звезд и красных карликов величина е может быть и существенно больше, порядка 1014 см2 ⋅ сек-3.
Перейдем теперь к случаю акустической турбулентности. Здесь, кроме того же основного параметра ε - диссипации энергии, есть еще один определяющий параметр: vs - скорость распространения звуковых волн. Из четырех величин с размерностями, зависящими только от длины и времени:
![$$
\begin{array}{l}
[\epsilon] = \mbox{см}^2 \cdot \mbox{сек}^{-3},\\ {[l]} = \mbox{см} \\
{[v_s]} = [v_l] = \mbox{см} \cdot \mbox{сек}^{-1},
\end{array}
$$](https://images.astronet.ru/pubd/2013/03/01/0001281314/tex/formula396.gif)
|
(5.93) |
можно составить два безразмерных комплекса и, следовательно, на основании одних соображений анализа размерностей нельзя получить спектр акустической турбулентности. Но это можно все же сделать, используя некоторые дополнительные физические соображения.
Во-первых, надо учесть, что если в вихревой турбулентности каждый вихрь живет примерно столько времени, сколько нужно веществу, чтобы совершить один полный оборот (т. е. в вихревой турбулентности характерное время τ ∼ l/vl), то в акустической турбулентности волна существует несколько или даже много периодов. Иными словами, здесь характерное время движения в масштабе l должно быть много больше величины "времени обращения", т. е. величины l/vl.
Взаимодействие волн между собой определяется их нелинейностью, т. е. величиной отношения vl/vs. Будем, поэтому считать, что в первом приближении характерное время взаимодействия τ больше времени обращения на множитель порядка большой величины отношения vs/vl т. е.
|
|
(5.94) |
Поток энергии через "иерархию волн", рассчитанный на единицу массы, очевидно, равен
|
|
(5.95) |
По-прежнему будем считать, что турбулентность определяется только передачей энергии от одних масштабов к другим и что диссипация энергии в тепло происходит в самых малых масштабах. Тогда величину ε можно считать постоянной, и поэтому
|
|
(5.96) |
Спектральная функция акустической турбулентности [16]:
|
|
(5.97) |
Минимальный масштаб (минимальная длина волны) определяется соотношением (5.89).
Анализ спектров акустической (млн магнитозвуковой) турбулентности в астрофизических условиях пока еще не проводился. Поэтому мы ограничимся лишь некоторыми качественными замечаниями. Соотношение (5.96), так же как и (5.86), можно использовать для оценки энергии турбулизации. Сравнивая эти формулы, видим, что в случае звуковой турбулентности необходим меньший расход энергии на возбуждение движений с теми же скоростями и в тех же масштабах, что и в случае вихревой турбулентности. Это означает, что если перенос энергии в атмосфере звезды определялся бы волнами, то величина (5.92) была бы меньше на множитель v0/vs. На Солнце действительно имеется перенос энергии волнами, но нужно иметь в виду, что таким путем переносится лишь небольшая часть полного потока энергии Солнца, т. е. та часть, которая расходуется на нагрев хромосферы и короны.
Задавая и в этом случае поток энергии Fa (который теперь много меньше величины L/4πR2), получим вместо (5.91)
|
|
(5.98) |
поскольку теперь энергия переносится со скоростью звука. Подставляя (5.90) и (5.98) в (5.96), находим
|
|
(5.99) |
с точностью до множителей порядка единицы.
Из сопоставления (5.92) и (5.99) можно сделать следующее заключение. Пусть у нас есть конвекция в виде турбулентности вихревого типа, которая на некотором уровне превращается в звуковую турбулентность. Тогда очевидно, что па этом уровне величины (5.92) и (5.99) должны быть одного порядка. Приравнивая эти величины, находим поток энергии, переносимый волновой турбулентностью:
|
|
(5.100) |
Для солнечной атмосферы имеем Fa ≈ 107 эрг ⋅ см-2 ⋅ сек-1 в удовлетворительном качественном согласии с данными наблюдений.
Хромосферы, нагреваемые волновой турбулентностью, вероятно, есть и у других звезд. Можно оценить параметры звезды, у которой хромосферная светимость La будет порядка фотосферной светимости. Имеем
|
|
(5.101) |
где, по-прежнему, р и ρ - давление и плотность в области генерации волновой турбулентности. Поэтому благоприятными являются условия в красных карликах, у которых действительно обнаружены хромосферные линии.
Свойства турбулентности часто определяют числом Рейнольдса для данного масштаба движений. Для вихревой и акустической турбулентности соответственно имеем
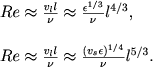
|
Величина числа Рейнольдса есть отношение времени диссипации движений из-за вязкости ∼ l2/v к характерному времени изменения состояния движения в масштабе l, т. е. величине l/vl ≈ l2/vll.
Число Рейнольдса максимально в области движений основного масштаба и минимально в области масштабов вязкой диссипации энергии. Если формально в выражении для числа Рейнольдса подставить l из (5.89), то получим, что в области масштабов вязкой диссипации Re ≈ 1. Однако многочисленные экспериментальные данные показали, что диссипация энергии турбулентных движений в тепловую из-за действия вязкости начинается при существенно больших масштабах. Оказалось, что в области наибольшей диссипации число Рейнольдса около 30-50. Отсюда, во-первых, следует, что значение минимального масштаба спектра Колмогорова порядка (15-25) (ν3/ε)1/4. Во-вторых, это обстоятельство позволяет получить численную оценку величины так называемой турбулентной вязкости. Это явление заключается в следующем.
Распад движений основного масштаба на более мелкомасштабные движения можно описать с помощью диссипации крупномасштабных движений под действием турбулентной вязкости. Здесь мелкомасштабные движения играют роль "молекул" с длиной свободного пробега l и скоростью движения vl. Величину турбулентной вязкости νt выбирают так, чтобы число Рейнольдса для турбулентной вязкости
|
|
(5.102) |
тоже было бы около 30-50.
Если турбулентность происходит в электропроводящей среде, где есть хотя бы слабые магнитные поля, то она оказывается тесно связанной с магнитным полем. В частности, много внимания в астрофизике уделялось усилению магнитного поля турбулентностью (турбулентное динамо). Этой проблеме посвящен, например, обзор С. И. Вайнштейна и Я. Б. Зельдовича [17]. Приведем лишь краткую сводку полученных в этом направлении результатов.
Прежде всего было показано, что турбулентные движения могут усиливать первоначальное (затравочное) магнитное поле, если эта турбулентность гиротропна, т. е. если среднее значение скалярного произведения скорости на ее ротор не равно нулю. Наглядно этот эффект сводится к геометрии движений, когда магнитная петля "перехлестывается и складывается", что и приводит к росту плотности магнитных силовых линий.
Рост магнитного поля определяется параметром гиротропности:
|
|
(5.103) |
где τl - характерное время корреляции движений (время распада или затухания движения в соответствующем масштабе). Магнитное поле усиливается в тех масштабах, где параметр αl не мал по сравнению со скоростью vl.
Например, характерное время усиления магнитного поля в акустической турбулентности:
|
|
(5.104) |
т. е. больше времени перекачки энергии между волнами разных масштабов в (vs/vl)2 раз.
В обзоре [17] в основном, рассматривается случай, когда даже усиленное магнитное поле остается настолько слабым, что не меняет существенно свойства турбулентности.
Случай, когда плотности кинетической и магнитной энергии в одних и тех же масштабах движения сравнимы, до сих пор не удалось рассмотреть с необходимой уверенностью в правильности полученных результатов, несмотря на большие усилия, предпринятые для решения этой очень важной для астрофизики проблемы.
Качественно можно указать на следующие соображения. Если магнитное поле В очень сильное, то вихревые движения подавлены, и турбулентность тогда может возникнуть лишь в виде совокупности альвеновских и магнитозвуковых волн. Свойства такой турбулентности близки к свойствам акустической турбулентности и будут справедливы соотношения (5.96) и (5.97), в которых скорость звука следует заменить на альвеновскую скорость ![]() . Получим для скорости, соответствующей амплитудам колебаний газа:
. Получим для скорости, соответствующей амплитудам колебаний газа:
|
|
(5.105) |
и для спектральной плотности энергии
|
|
(5.106) |
Если же магнитное поле таково, что плотность его энергии в больших масштабах несколько меньше, чем плотность кинетической энергии, то такое магнитное поле как бы подавляет движение в мелких масштабах и спектр становится более крутым, [14]. В работе [17] из эвристических соображений получен спектр движений
|
|
(5.107) |
Спектр такого типа получается вообще в тех случаях, когда энергия движения крупных масштабов не переходит в мелкомасштабные движения, например, если она диссипирует в крупномасштабных ударных волнах (см. [14] и [18]).
В книге Б. Б. Кадомцева [19] дано ясное и физически наглядное описание свойств турбулентности в различных условиях.
После этого обсуждения общих свойств турбулентности можно перейти к анализу конвекции.
Нам уже известно, что конвекция возникает тогда,, когда слой газа должен перенести достаточно большой поток энергии снизу вверх (против направления ускорения силы тяжести), а лучистая или другие виды теплопроводности не в состоянии этого сделать, например, из-за слишком большой непрозрачности. При конвекции внизу этого слоя образуются более нагретые элементы газа, которые всплывают вверх, перенося избыток тепло-вой энергии, отдают его в верхней части слоя и затем опускаются вниз уже холодными элементами. Таким образом, конвекцию можно охарактеризовать скоростью конвективных элементов и длиной их пробега. Эти две величины позволяют вычислить числа Рейнольдса, - как правило, в космических условиях они оказываются очень большими, достигая значений порядка 1010 или даже больше. Именно поэтому можно ожидать, что астрофизическая конвекция в большинстве случаев должна быть турбулентной. Сначала избыток тепла в нижнем слое передается движениям типа больших вихрей, которые существуют не больше, чем время движения газа по окружности вихря и поэтому не успевают донести избыток тепла до верхней границы слоя. Крупномасштабные вихри распадаются на мелкомасштабные, вся область турбулентной конвекции состоит из большого числа разномасштабных вихрей и поток тепла лишь последовательно передается от нижней границы слоя к верхней. Пели же число Рейнольдса невелико, то возникает ламинарная конвекция, которая имеет другой характер. Здесь движение газа более плавное, оно контролируется, с одной стороны, всплыванием конвективных элементов из-за избытка тепла, а с другой стороны, торможением этого движения из-за вязкости и теплопроводности. В подобной конвекции движение стационарно, вместо большого количества разномасштабных вихрей образуются более или менее одинаковые, расположенные правильным, образом, конвективные ячейки, высота которых равна толщине конвективной зоны, а их горизонтальный размер связан с высотой определенным соотношением. В пределах одной и той же ячейки газ может совершить много оборотов прежде, чем ячейка исчезнет. Можно считать, что в идеальном случае стационарный слой ламинарной конвекции состоит из стационарных ячеек, в которых газ течет по замкнутым линиям тока, нагреваясь внизу и охлаждаясь вверху. Такие ячейки имеют правильную форму, чаще всего шестиугольных призм.
Теория ламинарной конвекции была достаточно полно развита применительно к конвекции в однородном слое несжимаемой жидкости (см. подробное изложение в книге Чандрасекара [20]), но эти результаты можно использовать и для анализа конвекции в сжимаемом и неоднородном слое газа, если только на вертикальном протяжении слоя плотность газа не меняется существенным образом. Это соответствует случаю так называемого приближения Буссинеска. Рассмотрим этот случай более подробно.
Ламинарная конвекция описывается рядом безразмерных чисел, которые можно получить и пз соображений анализа размерностей. Разумеется, для нахождения соотношений между безразмерными параметрами один анализ размерностей недостаточен и приходится использовать уравнения движения. В соответствии с целью этой книги мы получим безразмерные комплексы ламинарной конвекции на основе теории размерностей и подобия, а затем приведем и некоторые соотношения между различными безразмерными комплексами, характеризующими ламинарную конвекцию.
Начнем со случая конвекции в среде, где нет вращения и магнитного поля, и где каждый конвективный элемент газа непрозрачен. Иными словами, будем считать, что обмен энергией между поднимающимися и опускающимися потоками газа происходит преимущественно на поверхности раздела этих потоков. Все эти ограничения будем потом снимать по очереди.
Найдем определяющие параметры такой задачи. Для этого напомним физику конвективного движения. Пусть есть некоторый градиент температуры (температура падает снизу вверх). Тогда, если какой-то элемент газа поднимается, то он, оказавшись в слое с меньшей температурой, расширяется из-за уменьшения внешнего давления и при этом станет менее плотным. Оказавшись легче окружающих слоев, конвективный элемент газа продолжает подъем, пока он не дойдет до верхней границы конвективного слоя, где избыток тепла будет отдан верхним слоям. Очевидно, что эффект переноса энергии определяется следующими явлениями: теплопроводностью; силой, заставляющей газ двигаться, т. е. силой Архимеда, и силой, тормозящей движение, т. е. вязкостью. Эти соображения позволяют найти определяющие параметры.
Сила Архимеда есть произведение ускорения силы тяжести на изменение плотности бр нагретого элемента газа по сравнению с окружающей средой. Мы будем относить все силы к единице массы и поэтому относительная сила Архимеда есть - g(δρ/ρ). Плотность газа уменьшается из-за его нагревания и поэтому лучше изменение плотности выразить через избыток температуры δ T. Если ввести коэффициент теплового расширения а, то имеем δρ/ρ = -αδT. В идеальном газе коэффициент теп- лового расширения определяется очень простой формулой: α = 1/T. Наконец, избыток температуры δ T следует выразить через так называемый сверхадиабатический температурный градиент:
|
|
(5.108) |
где dT/dz - средний градиент температуры в слое, (dT/dz)ad - адиабатический градиент температуры в поднимающемся элементе газа. Конвекция возможна только если β > 0. Именно сверхадиабатический градиент и определяет относительную "легкость" поднимающихся конвективных элементов.
Таким образом, параметр, характеризующий силу Архимеда при конвекции, можно записать в виде
|
|
(5.109) |
где l - толщина конвективной зоны. Два других определяющих параметра - вязкость и теплопроводность, - характеризуются коэффициентами кинетической вязкости ν и температуропроводности χ . Оба коэффициента имеют одинаковую размерность
|
|
(5.110) |
Из-за одинаковой размерности существует некоторая неопределенность в использовании этих коэффициентов, но, как оказалось, здесь все_определяется их средним геометрическим значением ![]() . Определяющим параметром является и толщина конвективного слоя. Итак, имеем следующий набор определяющих параметров:
. Определяющим параметром является и толщина конвективного слоя. Итак, имеем следующий набор определяющих параметров:
![$$
\begin{array}{l}
[g\alpha\beta l] = \mbox{см} \cdot \mbox{сек}^{-2},\\ {[\sqrt{\nu\chi}]} = \mbox{см}^2 \cdot \mbox{сек}^{-1} \\
{[l]} = \mbox{см}.
\end{array}
$$](https://images.astronet.ru/pubd/2013/03/01/0001281314/tex/formula415.gif)
|
(5.111) |
Отсюда сразу находим безразмерный комплекс - число Рэлея:
|
|
(5.112) |
Легко убедиться, что число Рэлея есть обратное отношение квадратов характерного времени всплывання и времени диссипации.
Поэтому число Рэлея соответствует квадрату числа Рейнольдса для конвективного движения. Это означает, что численное значение (5.112) для случая ламинарной конвекции должно быть порядка 103, поскольку соответствующее число Рейнольдса для движений определяемых вязкостью, порядка 30.
Задачу о вычислении числа Рэлея можно решить точно в простом случае однородной несжимаемой жидкости. Приведем здесь этот расчет, хотя, конечно, астрофизические условия далеки от случая несжимаемой жидкости.
Будем рассматривать стационарные движения поднимающегося элемента газа. Уравнения движения запишутся в виде:
|
|
(5.113) |
Здесь ![]() - вектор скорости, Δ - оператор Лапласа, δp - избыток давления в поднимающемся элементе газа. Первое уравнение есть обычное уравнение движения с вязкостью и архимедовой силой, второе уравнение есть уравнение температуропроводности в движущейся среде.
- вектор скорости, Δ - оператор Лапласа, δp - избыток давления в поднимающемся элементе газа. Первое уравнение есть обычное уравнение движения с вязкостью и архимедовой силой, второе уравнение есть уравнение температуропроводности в движущейся среде.
Будем решать (5.113) последовательными приближениями. В первом приближении опустим все члены с ![]() , δp и δρ. Первое уравнение будет удовлетворено автоматически, второе уравнение, при условии, что температура зависит только от вертикальной координаты z, дает
, δp и δρ. Первое уравнение будет удовлетворено автоматически, второе уравнение, при условии, что температура зависит только от вертикальной координаты z, дает
|
|
(5.114) |
где T0 - температура на нижней границе слоя. Здесь β есть некоторая постоянная, определяющая стационарный градиент температуры в слое. Очевидно, что при стационарной конвекции величина β есть сверхадиабатический температурный градиент (5.108). В следующем приближении учтем в (5.114) изменение температуры в поднимающихся и опускающихся элементах, т. е. запишем
|
|
(5.115) |
Подставим (5.115) во второе уравнение (5.113) и получим, сохранив лишь члены первого порядка малости,
|
|
(5.116) |
В первом уравнении заменим δρ/ρ на α(δT). Левая часть - второго порядка малости, ее можно опустить и в этом приближении. Чтобы исключить член ![]() , применим к этому уравнению операцию ротора. Тогда получим
, применим к этому уравнению операцию ротора. Тогда получим
|
|
(5.117) |
Еще раз применим к этому уравнению операцию ротора и учтем, что в случае несжимаемой жидкости ![]() , так как здесь
, так как здесь ![]() . Тогда получим вместо (5.117)
. Тогда получим вместо (5.117)
|
|
В этом уравнении представляет интерес лишь вертикальная компонента. Вычисляя второй член уравнения, находим
|
|
(5.118) |
Наконец, подставим в (5.118) величину vz из (5.116) и получим следующее уравнение для избытка температуры в поднимающихся и опускающихся элементах газа:
![$$
\Delta\Delta\Delta\delta T = \left[\left(\frac{\partial^2}{\partial x^2} + \frac{\partial^2}{\partial y^2} + \frac{\partial^2}{\partial z^2}\right)^3\delta T\right] = \frac{\alpha\rho g}{\chi\nu} \left[\left(\frac{\partial^2}{\partial y^2} + \frac{\partial^2}{\partial z^2}\right)\delta T\right].
$$](https://images.astronet.ru/pubd/2013/03/01/0001281314/tex/formula427.gif)
|
(5.119) |
Любопытно, что здесь понадобилось три раза использовать оператор Лапласа.
Теперь осталось сформулировать граничные условия. Здесь возможна различная постановка задач. Во-первых, во всех случаях на границе должно быть vz = 0, а следовательно, и δ T = 0. Вещество не может проникнуть через границы конвективной зоны. Если граница жесткая, то в силу действия вязкости на границах и vy = vx = 0, а из условия ![]() отсюда следует ∂vz/∂z = 0. Из (5.116) тогда находим и ∂(δT)/∂z = 0. Но на свободных границах возможны горизонтальные движения вещества. Здесь граничные условия требуют обращения в нуль касательных натяжений, т. е. величин ∂vy/∂z + ∂vz/∂y и ∂vx/∂z + ∂vz/∂x откуда следует граничное условие ∂²vz/∂t² = 0. Мы будем исследовать случай, когда как нижнюю, так и верхнюю границы конвективной области можно рассматривать как свободные поверхности, а поэтому примем, что на обеих границах
отсюда следует ∂vz/∂z = 0. Из (5.116) тогда находим и ∂(δT)/∂z = 0. Но на свободных границах возможны горизонтальные движения вещества. Здесь граничные условия требуют обращения в нуль касательных натяжений, т. е. величин ∂vy/∂z + ∂vz/∂y и ∂vx/∂z + ∂vz/∂x откуда следует граничное условие ∂²vz/∂t² = 0. Мы будем исследовать случай, когда как нижнюю, так и верхнюю границы конвективной области можно рассматривать как свободные поверхности, а поэтому примем, что на обеих границах
|
|
(5.120) |
Вернемся к уравнению (5.119) и будем искать его решение в виде
|
|
(5.122) |
где k2 = kx2 + ky2, при следующих граничных условиях:
|
|
(5.123) |
Но из уравнения (5.122) сразу следует, что при условиях (5.123) на границах равны нулю вообще все производные четного порядка, т е.
|
|
(5.124) |
Это означает, что решением уравнений (5.122), (5.123) может быть только выражение
|
|
(5.125) |
где А - произвольная постоянная. Подставим (5.125) в (5.122) и, обозначая
|
|
(5.126) |
получим отсюда
|
|
(5.127) |
Обсудим теперь полученное решение. Очевидно, что наибольшему масштабу движения соответствует случай n = 1. При n > 1 вертикальная компонента скорости обращает знак внутри слоя, т. е. здесь движения имеют масштаб l/n. Примем поэтому n = 1. Далее легко определить, что (5.127) минимально, если а = π/√2. Тогда
|
|
(5.128) |
Таким образом, ламинарная конвекция наступает тогда, когда сверхадиабатический градиент будет больше, чем
|
|
(5.129) |
Здесь появляются правильные ячейки с горизонтальным размером
|
|
(5.130) |
т. е. примерно в три раза большим, чем толщина конвективного слоя. Если увеличивать сверхадиабатический температурный градиент, то увеличивается и число Рэлея. При этом растет а, т. е. уменьшаются горизонтальные размеры ячейки, а затем увеличиваются и n. Это и означает переход к турбулентной конвекции.
Выше мы получили решение для случая свободных границ. Если границы жесткие, число Рэлея больше и равно 1700 [20]. Таким образом, точная теория ламинарной конвекции подтверждает опытные данные о том, что число Рейнольдса для наименьших вихревых движений не может быть слишком малым; оно порядка ![]() ≈ 25.
≈ 25.
Аналогичным образом решается задача о расчете числа Рэлея для конвекции с учетом вращения и магнитных полей. Подробно эти проблемы также рассмотрены Чандрасекаром [20]. Мы приведем здесь только некоторые окончательные формулы.
Предположим, что конвективный слой вращается относительно вертикального направления с угловой скоростью Ω;;;. Тогда появляется еще один размерный определяющий параметр с размерностью [Ω;;;] = сек-1 и, следовательно, еще один безразмерный комплекс, который можно выбрать в виде
|
|
(5.131) |
Величина T называется числом Тейлора. Очевидно, что между числами Рэлея и Тейлора существует связь, которую также можно получить из общих уравнений движения. Оказалось [20], что
|
|
(5.132) |
Итак, вращение увеличивает число Рэлея, и, следовательно, затрудняет наступление конвекции. Если угловая скорость вращения очень велика, т. е. если T ≫ 1, то
|
|
(5.133) |
Характер движения частиц газа в конвекции во вращающемся слое изображен на рис. 21. Чем больше Т, тем больше закручивание спиралей, т. е. тем меньше расстояние между соседними витками.
Учет влияния магнитного поля вносит еще два параметра: магнитную индукцию B и магнитную вязкость νm. Размерность магнитной вязкости совпадает с размерностью обычной вязкости и поэтому независимым по размерности является только параметр [B]= г ⋅ см1/2 ⋅ сек-1.
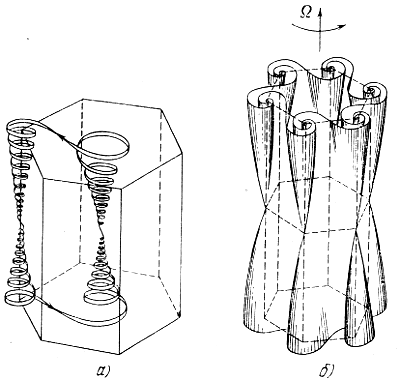
Рис. 21. Движение частиц (a) и структура конвективных шестиугольных ячеек (б) в случае конвекции в слое несжимаемой жидкости, находящемся в быстром вращении вокруг вертикальной оси (согласно Чандрасекару),
Поскольку появилась размерность массы, включим в число определяющих параметров и плотность ρ , а точнее, будем считать определяющим параметром комбинацию [B²/4πρ] = см2 ⋅ сек-2. В результате образуется еще одно безразмерное число
|
|
(5.134) |
введенное Чандрасекаром, но оставшееся без названия.
Если в конвективном слое есть вертикальное магнитное поле, но нет вращения, то связь между R и Q имеет вид
|
|
(5.135) |
В очень сильных магнитных полях Q ≫ 1:
|
|
(5.136) |
Можно показать, что горизонтальное магнитное поле не влияет на конвекцию, а сильное вертикальное поле, как следует из (5.136), затрудняет наступление конвекции (растет β) и приводит к тому, что конвективные элементы из призм со стороной основания больше высоты превращаются в тонкие столбы, которые в пределе Q → ∞ стремятся к бесконечно тонким нитям.
Совместное действие вращения и магнитного поля приводит к соотношению
|
|
(5.137) |
Этот случай также подробно изучен Чандрасекаром.
Наконец, учтем влияние прозрачности конвективных элементов. Это обобщение на случай конвекции без магнитного поля было дано Шпигелем (см. обзор [21]), а с учетом влияния магнитного поля - С. А. Капланом. Приведем основные результаты. Пусть τl есть оптическая толща всего конвективного слоя, т. е.
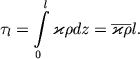
|
(5.138) |
Тогда, как можно показать, учет возможной прозрачности конвективных элементов приводит к замене левой части для числа Рэлея (5.127) на величину
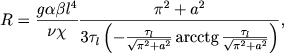
|
(5.139) |
причем под χ теперь следует понимать лучистую температуропроводность, которая связана с коэффициентом непрозрачности ϰ соотношением
|
|
(5.140) |
где cv - теплоемкость при постоянном объеме, σ - постоянная закона Стефана - Больцмана. Второе соотношение основано на представлении, что ![]() есть длина свободного пробега кванта, а с - его скорость.
есть длина свободного пробега кванта, а с - его скорость.
Правая часть R равна любому из выражений (5.127), (5.132), (5.133), (5.135) - (5.137) в зависимости от условий конвекции. Из определения (5.139) следует, что в том случае, когда оптический размер конвективного элемента велик,
|
|
(5.141) |
второй множитель (5.139) близок к единице и конвекция обладает теми же свойствами, что п.в непрозрачном случае. Однако, если имеет место обратное неравенство, которое возможно и при большой оптической толще слоя, т. е. τl ≫ 1 , если только параметр а большой, а именно, когда
|
|
(5.142) |
то влияние прозрачности существенно. Заметим, что величина (5.142) есть оптический диаметр конвективного элемента. Ясно, что если этот элемент имеет вид тонкой нити, как в случае сильного магнитного поля, то оптический диаметр ϰρl/a может быть и меньше единицы, хотя оптическая толща всего конвективного слоя ![]() и много больше единицы.
и много больше единицы.
В случае прозрачной конвекции без магнитного поля (т. е. при приравнивании (5.113) и (5.122)) и условии τl ≪ 1, получим
|
|
(5.143) |
Здесь конвективные элементы, по-прежнему, имеют вид призм, у которых сторона основания сравнима с высотой. Величина сверхадиабатического градиента оказывается много меньше чем в непрозрачном слое (в ![]() раз).
раз).
Сильное вертикальное магнитное поле и здесь вытягивает конвективные элементы. Q ≫ 1, то получим из условий (5.139) и (5.135)
|
|
(5.144) |
Условие прозрачности конвективных элементов по диаметру:
|
|
(5.145) |
Напомним, что оптическая толща всего конвективного слоя может быть и велика. Для сверхадиабатического градиента такой конвекции будем иметь:
|
|
(5.146) |
или, полагая α = 1/T и ![]()
|
|
(5.147) |
Это соотношение справедливо только при условии (5.145), т. е.
|
|
(5.148) |
При очень большой непрозрачности слоя и сильном магнитном поле сверхадиабатический градиент, согласно (5.136),
|
|
(5.149) |
Учет прозрачности конвективных "нитей" при сильном магнитном поле ослабляет подавление конвекции магнитным полем, в частности, в прозрачной конвекции β ∼ B, а в непрозрачной β ∼ B².
Дальнейшее обобщение теории связано с учетом более быстрого изменения давления в конвективном слое. Например, если считать, что давление в конвективном слое падает с высотой по барометрической формуле с эквивалентной высотой Н, то для числа Рэлея получается выражение [22]:
![$$
R = \frac{\pi^2 + a^2 + (l/2H)^2}{a^2}\left[\left(\pi^2 + a^2 + \frac{l^2}{4H^2}\right)^2 - \frac{2}{3}\left(\frac{al}{H}\right)^2\right].
$$](https://images.astronet.ru/pubd/2013/03/01/0001281314/tex/formula462.gif)
|
(5.150) |
Если толщина конвективного слоя много больше эквивалентной высоты (l ≫ H), то горизонтальный размер конвективных ячеек и величина сверхадиабатического градиента определяются только эквивалентной высотой. Здесь
|
|
(5.151) |
т. е. сторона основания конвективных призм порядка (2-3) Н, а сверхадиабатический градиент
|
|
(5.152) |
Возможны и другие обобщения.
Выше очень подробно был описан случай ламинарной конвекции для среды с однородной плотностью Разумеется, с точки зрения астрофизических применений теории такой случай является далеко идущей идеализацией. Например, на Солнце конвекция имеет место в слое, плотность внутри которого меняется на несколько порядков величин. Поэтому описанная выше теория к реальным астрофизическим объектам, строго говоря, неприменима. Тем не менее и она представляет для астрофизики определенную ценность. Во-первых, характерные числа R, Т, Q и τd получены из соображений размерности и поэтому их можно использовать во всех случаях. Точные связи между этими числами зависят, конечно, от идеализированной постановки задачи, но качественные характеристики и асимптотическое поведение имеют более общий характер. Поэтому для оценок эффектов влияния вращения, магнитного поля, прозрачности вихрей на уровне конвекции всеми этими соотношениями вполне можно пользоваться.
Впрочем, основной целью столь подробного изложения была иллюстрация тех возможностей, которые дает теория анализа размерностей и подобия в этой проблеме.
Ведь все полученные здесь связи между безразмерными комплексами и есть следствия П-теоремы.
Но возвратимся к реальной астрофизической конвекции. Как уже было подробно изложено в предыдущей главе, конвекция играет очень большую роль в переносе энергии в недрах звезд - в центральных конвективных ядрах горячих звезд и в конвективных зонах под поверхностью холодных звезд. Здесь конвекция имеет преимущественно турбулентный характер. Достаточно удовлетворительной теории такой конвекции еще нет. Поэтому приходится прибегать к различным полукачественным моделям.
Можно использовать и приведенные выше модели стационарной ламинарной конвекции, если вместо обычной вязкости подставить турбулентную вязкость. Тогда можно изучить, например, влияние магнитных полей и вращения на величину сверхадиабатического градиента. Величина турбулентной вязкости подбирается так, чтобы число Рейнольдса было бы порядка 30, а следовательно, число Рэлея без учета магнитных полей - около 10³.
Очень часто используется метод длины перемешивания. В этом методе заранее задается высота подъема конвективных элементов l, называемая длиной перемешивания. Тогда легко определить скорость подъема конвективного элемента под действием силы Архимеда:
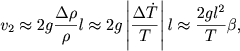
|
(5.153) |
предполагая движение равноускоренным. Поток энергии, переносимый конвекцией,
|
|
(5.154) |
где cp - теплоемкость при постоянном давлении. Формула (5.154), в отличие от (5.91), описывает поток тепловой энергии, переносимой конвекцией. К этим уравнениям добавляется также уравнение теплопроводности типа (5.116), что и позволяет получить систему уравнений, определяющих параметры конвективной области.
При расчетах задается Fконв и l. Величина Fконв определяется потоком энергии, который должен быть перенесен в этой зоне, а величину l часто выбирают равной эквивалентной высоте слоя или другим параметрам с размерностью длины.
Метод длины перемешивания допускает только численное решение. Было построено много различных моделей, и в теории внутреннего строения звезд или теории конвективной зоны Солнца эти модели играют очень большую роль. Но с точки зрения теории подобия и анализа размерностей эти модели не обсуждались. Это трудно сделать, поскольку здесь нет аналитических соотношений.
Наконец, в теории турбулентной конвекции использовался и метод построения спектральных уравнений. Как мы уже отмечали, турбулентность описывается спектральной функцией Wk (см. (5.87), (5.97), (5.107)). Можно попытаться сразу составить уравнения для этой функции. Строгого метода получения таких уравнений нет, но можно воспользоваться различными эвристическими соображениями, где не последнюю роль играют и соображения анализа размерностей.
Например, Леду, Шварцшильд и Шпигель [23] предложили следующее интегральное уравнение для нахождения спектральной функции турбулентной конвекции:
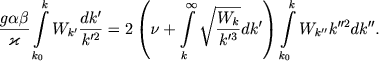
|
(5.155) |
Здесь k0 = 2π/l0 - волновое число основного масштаба конвективной зоны. В левой части стоит величина, определяющая силу всплывания, действующую на все конвективные элементы с масштабами большими, чем 2π/k. Правая часть определяет действие вязкости, в том числе и турбулентной, описываемой членом
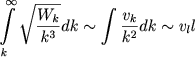
|
(5.156) |
согласно предположению Гейзенберга.
В это уравнение можно ввести и члены, описывающие действие магнитного поля на конвекцию (см. [17]).
Тогда в правой части добавится слагаемое
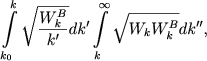
|
(5.157) |
где ![]() - спектральная плотность магнитной энергии, т. е. распределение флуктуации величины магнитного поля по разным масштабам. Такой вид этого члена определяется тем, что первый множитель представляет собой как бы "магнитную вязкость" турбулентного движения. Различие между (5.156) и (5.157) заключается в следующем - турбулентная вязкость определяется тем, что мелкомасштабные движения забирают энергию от крупномасштабных, а магнитное поле действует наоборот - более сильное крупномасштабное поле подавляет движение мелкомасштабных полей. Вид второго множителя определяется соображениями анализа размерностей и тем, что магнитная сила всегда пропорциональна
- спектральная плотность магнитной энергии, т. е. распределение флуктуации величины магнитного поля по разным масштабам. Такой вид этого члена определяется тем, что первый множитель представляет собой как бы "магнитную вязкость" турбулентного движения. Различие между (5.156) и (5.157) заключается в следующем - турбулентная вязкость определяется тем, что мелкомасштабные движения забирают энергию от крупномасштабных, а магнитное поле действует наоборот - более сильное крупномасштабное поле подавляет движение мелкомасштабных полей. Вид второго множителя определяется соображениями анализа размерностей и тем, что магнитная сила всегда пропорциональна ![]() . Поскольку теперь есть две неизвестные спектральные функции, то следует записать два уравнения вида (5.155). Вид второго уравнения зависит от того, как действует архимедова сила на магнитное поле. Мы сейчас не будем заниматься обсуждением этого метода исследования турбулентной конвекции. Упомянем только результаты. В области больших масштабов, соответствующих толщине конвективной зоны, спектральная функция
. Поскольку теперь есть две неизвестные спектральные функции, то следует записать два уравнения вида (5.155). Вид второго уравнения зависит от того, как действует архимедова сила на магнитное поле. Мы сейчас не будем заниматься обсуждением этого метода исследования турбулентной конвекции. Упомянем только результаты. В области больших масштабов, соответствующих толщине конвективной зоны, спектральная функция
|
|
(5.158) |
чему соответствует соотношение ![]() . Это означает, что почти вся энергия движения сосредоточена в области самых крупных масштабов, что качественно соответствует описанной выше картине ламинарной конвекции. В области меньших масштабов, но без учета магнитного поля,
. Это означает, что почти вся энергия движения сосредоточена в области самых крупных масштабов, что качественно соответствует описанной выше картине ламинарной конвекции. В области меньших масштабов, но без учета магнитного поля,
|
|
(5.159) |
т. е. появился спектр Колмогорова. Эта область масштабов определяет турбулентную вязкость. Наконец, в той области спектра, где сильно влияние магнитного поля
|
|
(5.160) |
Здесь спектр более крутой, чем без учета магнитного поля.
К сожалению, все эти методы имеют тот существенный недостаток, что, поскольку сами уравнения составляются с известной долей произвола, то и решения не имеют силы доказательств. В лучшем случае их можно рассматривать только как качественную характеристику явления.
Можно построить более строгую теорию, для конвекции в очень сильном магнитном поле. Здесь газ уже не может свободно двигаться по конвективной области и конвекция становится колебательной. Модель такой конвекции рассмотрел Ю. Д. Жугжда [24]. Если имеется градиент температуры вдоль магнитных силовых линий, то тепловая энергия может переноситься и при колебаниях газа в таком сильном магнитном поле. Задачу можно рассмотреть строго, но простых аналитических соотношений получить не удалось. Эта теория позволила объяснить сложную структуру тени и полутени солнечных пятен, а также и некоторые другие явления солнечной активности (см. обзор [25]). Конвекция в политропной атмосфере с магнитным полем изучалась в работе [26]. Здесь также удалось получить зависимость сверхадиабатического градиента температуры от напряженности магнитного поля.
В заключение еще раз подчеркнем, что в теории турбулентности и теории конвекции методы анализа размерностей и теории подобия оказались весьма эффективными, но, к сожалению, мы еще далеки от создания такой теории, которая удовлетворительно описывала бы астрофизические условия.
<< § 5.2 Вращение и магнитные поля звезд | Оглавление | § 5.4 Циркуляция в атмосферах планет >>