§ 1.4 Примеры применения анализа размерностей к астрофизическим задачам
Общий метод построения безразмерных комплексов и определения зависимостей между различными величинами проще всего сразу проиллюстрировать на конкретных примерах. И дело не только в том, что такие примеры в силу своей наглядности позволяют яснее понять сущность метода. Очень важно также и то, что в методах применения теории размерностей большую роль играет интуиция и поэтому здесь не всегда можно действовать в рамках формальных правил. Разумеется, формальное применение метода теории размерностей всегда дает правильные результаты, но не всегда именно то, что нас интересует.
Математическая сторона применения метода размерностей к конкретным задачам обычно сводится к решению очень элементарной алгебраической системы уравнений. Удобно для записи этих уравнений ввести матричное обозначение, предложенное Лангхааром (см. [5]). В дальнейшем мы будем часто приводить эти матрицы размерности в разных задачах.
Изложение теории размерностей часто начинают с описания решения задачи о колебании маятника. С подобной астрофизической задачи - проблемы пульсации звезд - начнем и мы. В простейшем случае линейного маятника пренебрегается амплитудой колебаний, считается, что она мала. Мы тоже будем считать амплитуду пульсаций звезд малой, т. е. рассмотрим линейные пульсации.
Как известно, пульсации звезд представляют собой периодические сжатия и расширения звезд, по-видимому, имеющие довольно строго выраженный радиальный характер. Как показывают наблюдения, амплитуда колебаний не более 5%, так что пульсации можно действительно считать линейными. Однако сами колебания несинусоидальны, время расширения и время сжатия неодинаковы. Строго говоря, линейные колебания должны быть синусоидальны, но наблюдаемые отклонения от этой симметрии могут быть объяснены явлениями в поверхностных слоях пульсирующих звезд, где относительная амплитуда колебаний не мала. Это приводит к относительному смещению фазы колебаний на разных глубинах и к искажению профиля колебаний. Как показывают расчеты, колебания в глубоких слоях пульсирующих звезд имеют более синусоидальный характер, и линейное приближение оказывается вполне достаточным, по крайней мере в первом приближении, которым мы в этом параграфе и ограничимся. Более тонкие эффекты будут обсуждены в гл. 5.
Здесь мы рассмотрим простейшую проблему теории пульсации звезд: определение периода колебаний в первом приближении. В рамках метода анализа размерностей будем исходить из набора трех основных параметров звезд: массы М, светимости L и радиуса R. Кроме того, очевидно, что сами пульсации тесно связаны с явлением всемирного тяготения, характеризуемым постоянной Ньютона G - ведь сжатие звезды при пульсации вызвано полем тяготения звезды. Наконец, в линейном приближении пульсации характеризуются только частотой или периодом Р. Таким образом, имеем пять основных, определяющих параметров: М, L, R, G, Р с размерностями:
|
|
(1.10) |
Достаточно ли этих параметров? Для полной теории пульсации звезд этого, конечно, недостаточно - известно, что одни звезды с одним и тем же набором параметров М, L, R не пульсируют, а другие пульсируют. Как было показано, например, С. А. Жевакиным еще в 1953 г., звезда с подходящим набором параметров М, L, R будет пульсировать только тогда, когда содержание гелия в ней не менее 15%, и когда коэффициент непрозрачности вещества такой, что возможно действие "клапанного" механизма, компенсирующего потери энергии при диссипации движений пульсаций. Очевидно, что пульсации звезд, а возможно, и точное значение периода, зависят от структуры звезды и от ее химического состава. Но, еще раз подчеркиваем, задача теории размерностей заключается не в том, чтобы дать ответ на вопрос, какова природа явления, а в том, чтобы, исходя только из размерностей величин, получить оценки параметров в предположении, что само явление имеет место.
Параметры (1.10) являются основными и они должны определить период пульсации звезд - если эти пульсации действительно имеют место. Другие параметры, в том числе и очень важные для возникновения пульсаций (химический состав, коэффициент непрозрачности, роль ионизации в поверхностных слоях, конвекция и т. п.), естественно, в какой-то степени влияют на величину периода, но уже в следующем приближении.
Запишем в неявном виде неизвестную нам формулу, связывающую параметры (1.10):
|
|
(1.11) |
Число независимых размерностей равно трем. Следовательно, согласно П-теореме есть два безразмерных комплекса, П1 и П2, и мы можем соотношение (1.11) переписать в виде:
|
|
(1.12) |
Для нахождения безразмерных комплексов П1 и П2 составим матрицу размерности:
![$$
\begin{matrix}
\, & [M] & [L] & [R] & [G] & [P] \\
\mbox{г}&1&1&0&-1&0 \\
\mbox{см}&0&2&1&3&0 \\
\mbox{сек}&0&-3&0&-2&1
\end{matrix}
$$](https://images.astronet.ru/pubd/2013/03/01/0001281314/tex/formula101.gif)
|
(1.13) |
Компоненты (матричные элементы) матрицы размерности есть показатели степеней, в которых единицы размерностей (перечисленные слева) входят в определяющие параметры (перечисленные сверху). Число столбцов равно числу определяющих параметров, число строк равно числу первичных основных единиц измерения.
Всякая матрица, в том числе и матрица размерности, характеризуется ее рангом, т. е. рангом наибольшего по числу строк и столбцов ненулевого детерминанта. В случае (1.13) отличен от нуля детерминант третьего ранга, составленный, например, из трех первых столбцов (или трех последних, это все равно). Следовательно, и ранг матрицы размерности здесь равен трем. Легко видеть, что всегда ранг матрицы размерности равен числу определяющих параметров с независимыми размерностями в полном наборе определяющих параметров. Ранг матрицы размерности не больше числа строк, но может быть и меньше. Как правило, этот случай можно заранее предусмотреть и не выписывать лишних строк.
В соответствии с определением формулы размерности (степенных зависимостей (1.1)) любой безразмерный комплекс в нашей задаче может быть записан в виде
|
|
(1.14) |
где k1, k2, k3, k4, k5 есть искомые показатели степени. Используя матрицу размерности, легко составить алгебраическую систему уравнений для определения этих показателей:
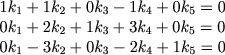
|
(1.15) |
Получилась система из трех уравнений для определения пяти неизвестных величин. Поскольку ранг матрицы равен трем, то отсюда следует, что два из искомых пяти показателей можно задавать произвольно. Тогда остальные величины ki получаются путем решения системы (1.15). Впрочем, надо иметь в виду, что хотя выбор двух значений параметров ki и произволен, но при этом следует все же руководствоваться некоторыми интуитивными физическими соображениями для того, чтобы потом безразмерным комплексам можно было бы приписать физический смысл, позволяющий получить их наглядную интерпретацию.
Для первого комплекса, который и должен определять период, выберем показатель при Р, т. е. k5, равным единице.
Теперь можно произвольно выбрать один из остальных показателей k1, k2, k3 или k4 равным нулю. Лучше всего сделать так, чтобы исключить один из основных параметров звезды М, L или R. Поскольку колебания механические, то кажется более важной зависимость от M и R Примем поэтому k2 = 0. Тогда решение системы (1.15) находится без труда и мы имеем k1 = k4 = 1/2, k3 = -3/2. Это и дает нам первый безразмерный комплекс:
|
|
(1.16) |
Здесь можно отделить астрофизические измеряемые величины от универсальных постоянных и, кроме того, воспользоваться определением средней плотности звезды ![]() . Тогда получим
. Тогда получим
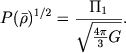
|
(1.17) |
Это есть хорошо известное в астрофизике соотношение "период - плотность" для пульсирующих звезд, если считать правую часть постоянной величиной. Используя наблюдательные данные, можно приближенно написать
|
|
(1.18) |
Смысл безразмерного комплекса (1.16) - (1.18) легко понять, используя аналогию с колебаниями маятника. Как известно из формулы Гюйгенса, период колебаний математического маятника длиной l в поле тяжести с ускорением g равен
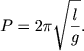
|
(1.19) |
Применим эту формулу к пульсациям звезд, приняв "длину" маятника равной радиусу звезды, т. е. l=R, и положив ускорение силы тяжести равным его значению на поверхности звезды, т. е. g = GMR-2. Опять вводя выражение для средней плотности ![]() , получим из (1.19) формулу
, получим из (1.19) формулу
|
|
(1.20) |
соответствующую (1.17) при значении безразмерного комплекса П1 = 2π.
Физическая суть явлений, соответствующих пульсациям звезд и колебаниям маятника, одна и та же - это механические движения в иоле тяжести, соответствующие небольшим отклонениям от положения равновесия. Отсюда и близость численных значений безразмерных комплексов и их примерное постоянство для объектов столь различных масштабов.
Второй безразмерный комплекс надо выбрать так, чтобы в него вошел хотя бы один из параметров, которого нет в первом комплексе; тогда автоматически обеспечивается их размерная независимость. В этом случае примем k2 = 1 и k4 = 0, т. е. сохраним светимость и опустим постоянную тяготения. Тогда решение системы (1.15) дает: k1 = -1, k3 = -2, k1 = 3, и мы получаем безразмерный комплекс:
|
|
(1.21) |
Физический смысл этой величины тоже простой: это есть отношение энергии, излученной звездой за один период колебания LP, к величине, которая характеризует механическую энергию колебаний звезд MR2/P2. Параметр П1 есть нечто вроде обратной величины добротности колебаний звезд, но нужно иметь в виду, что энергия, диссипировавшая за одно колебание, много меньше энергии, излученной звездой за это время, а величина кинетической энергии пульсаций также существенно меньше MR2/P2, так как пульсируют только наружные слои звезды (т. е. малая доля массы звезды) и амплитуда пульсаций мала по сравнению с радиусом звезды.
Сопоставляя соотношение (1.21) с данными наблюдений, легко убедиться, что, во-первых, безразмерный комплекс П2 всегда на порядки величин меньше единицы, а, во-вторых, у разных звезд его величина очень различна. В самом деле, у цефеид типа RR Лиры П2 ≈ (4 ÷ 80) ⋅ 10-9, а у классических цефеид этот комплекс меняется еще в больших пределах - от 10-9 до 3 ⋅ 10-3 по мере увеличения периода. Таким образом, в отличие от П1 величина П2 не может считаться постоянной. Но это условие также следует и из П-теоремы.
Согласно этой теореме формула (1.11) переписывается в виде
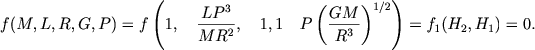
|
(1.22) |
Учитывая теперь, что П2 << 1, запишем:
|
|
(1.23) |
Отсюда следует, что в первом приближении решение уравнения f1(0, П1) = 0 дает некоторое постоянное значение лишь для П1 а величина П2 << 1 остается неопределенной и поэтому может сильно меняться у звезд разных типов и масс.
Таким образом, период пульсаций звезды зависит в первом приближении только от средней плотности. Явной зависимости периода от светимости здесь нет. Но, разумеется, есть неявная зависимость, поскольку светимости звезд тоже зависят от их массы и от средней плотности. И действительно, хорошо известна зависимость период-светимость у переменных звезд определенных типов, позволяющая использовать эти звезды для создания шкалы расстояний. К сожалению, соображения теории размерностей оказались недостаточными для получения и этой зависимости, но, еще раз подчеркиваем, соотношение период - средняя плотность получается из соображений размерности сразу.
Второй безразмерный комплекс мы выбрали более или менее произвольно. Возможен, конечно, и другой выбор этой величины. Но в любом случае его можно представить в виде произведения ![]() где а и b некоторые рациональные числа. Отсюда ясно, что в любом случае второй безразмерный комплекс будет либо очень мал либо велик (в таком случае надо перейти к обратной величине этого комплекса) и из П-теоремы по-прежнему следует только постоянство первого безразмерного комплекса.
где а и b некоторые рациональные числа. Отсюда ясно, что в любом случае второй безразмерный комплекс будет либо очень мал либо велик (в таком случае надо перейти к обратной величине этого комплекса) и из П-теоремы по-прежнему следует только постоянство первого безразмерного комплекса.
Выше мы сравнили пульсации звезд с колебаниями математического маятника. Оказалось, что основной безразмерный комплекс (критерий подобия) в обоих случаях имеет близкие значения. Это означает, что явление колебания звезд и явление колебания маятника подобны по основному параметру. Но, разумеется, во многом эти явления и существенно различны. Было построено много численных моделей звездных пульсаций, учитывающих и другие определяющие параметры (см. гл. 5), существенно отличные от параметров колебаний маятника. Здесь, разумеется, подобия нет.
В таких случаях можно говорить об ограниченном подобии явлений, когда совпадают численные значения лишь некоторых определяющих безразмерных комплексов, но другие безразмерные комплексы существенно различаются.
Второй пример выберем из теории движения тел в поле тяжести. Этот очень простой пример позволит продемонстрировать важный методический прием теории размерностей, - так называемое дополнение Хантли (см. [4]).
Рассмотрим хорошо известную из механики задачу. Пусть под углом α к поверхности брошено тело с начальной скоростью v0. Под действием ускорения силы тяжести g тело упадет обратно на поверхность на некотором расстоянии l от точки бросания. Требуется определить эту величину. Искомая зависимость есть
|
|
(1.24) |
Составим матрицу размерности:
![$$
\begin{matrix}
\, & [\alpha] & [v_0] & [g] & [l] \\
\mbox{см}&0&1&1&1 \\
\mbox{сек}&0&-1&-2&0
\end{matrix}
$$](https://images.astronet.ru/pubd/2013/03/01/0001281314/tex/formula116.gif)
|
Один из безразмерных комплексов очевиден - сама безразмерная величина α , т. е.
|
|
(1.25) |
Второй безразмерный комплекс ищем в виде ![]() , откуда находим
, откуда находим
|
|
(1.26) |
Следовательно, вместо (1.24) имеем
|
|
(1.27) |
Это соотношение можно переписать и в виде
|
|
(1.28) |
где φ(α) - некоторая неизвестная функция. Казалось бы, методом теории размерностей ее определить нельзя. Но оказывается, что это все же можно сделать, если считать горизонтальные (x) и вертикальные (у) координаты, имеющими разные размерности. Тогда и компоненты скорости v0x=v0sinα и v0y=v0cosα также имеют разные размерности. В этом случае матрица размерности:
![$$
\begin{matrix}
\, & [v_0x] & [v_0y] & [g] & [l] \\
x&1&0&0&1 \\
y&0&1&1&0 \\
\mbox{сек}&-1&-1&-2&0
\end{matrix}
$$](https://images.astronet.ru/pubd/2013/03/01/0001281314/tex/formula122.gif)
|
Этой матрице соответствует только один безразмерный комплекс
|
|
(1.28) |
откуда имеем
|
|
(1.30) |
Тем самым функция φ(α) в (1.28) оказалась определенной.
Метод приписывания фиктивной разной размерности величинам с одинаковыми физическими размерностями может оказаться полезным и в других случаях. Методами теории размерностей можно определить многие физические .параметры, необходимые для астрофизических исследований. Например, можно оценить размер атома водорода α0 и его энергию ионизации χH. Очевидно, что эти величины определяются массой электрона me и его зарядом е. Кроме того, поскольку атом водорода является квантовомеханической системой, в число определяющих параметров входит и постоянная Планка ħ . Таким образом, имеем следующую матрицу размерностей:
![$$
\begin{matrix}
\, & [a_0] & [\chi_H] & [m_e] & [e] & [\hbar] \\
\mbox{г}&0&1&1&1/2&1 \\
\mbox{см}&1&2&0&3/2&2 \\
\mbox{сек}&0&-2&0&-1&-1
\end{matrix}
$$](https://images.astronet.ru/pubd/2013/03/01/0001281314/tex/formula125.gif)
|
Как и раньше, ищем безразмерные комплексы в виде
|
|
(1.31) |
Решая систему соответствующих уравнений для показателей ki, находим два решения, причем в первом принимаем k1 = 1, k2 = 0, а во втором k1 = 0, k2 = 1. В результате получаем два комплекса:
|
|
Точная теория дает для численных значений безразмерных комплексов величины П1 = 1, П2=½ . Таким образом,
|
|
(1.32) |
Обе величины играют важную роль и в астрофизике.
Аналогичным образом можно найти характерный размер атомного ядра aN и величину энергии связи нуклонов в ядре χN. Для этого в соотношениях (1.32) следует заменить me на массу нуклона mN и ввести вместо е величину g, характеризующую ядерное взаимодействие.
Согласно Вайскопфу [13] потенциал притяжения между нуклонами на их среднем расстоянии в ядре может быть аппроксимирован электростатическим потенциалом с g ≈ 3,3е, т. е. g2 ≈ 10е2. Поэтому для характеристик атомного ядра получим вместо (1.32)
|
|
(1.33) |
Наконец, как последний пример, иллюстрирующий значение подобия в астрофизике, рассмотрим определение радиуса зон ионизации Стремгрена. Известно, что вокруг каждой горячей звезды в межзвездном газе образуется зона ионизованного водорода. Внутри ее водород почти полностью ионизован, вне ее - почти нейтрален. Граница зоны ионизации достаточно резкая. Во всяком случае толщина переходной области много меньше радиуса зон ионизации. Величину радиуса зон ионизации водорода s0 легко оценить, воспользовавшись тем условием, что внутри зоны Стремгрена число ионизации за единицу времени равно числу рекомбинаций за это же время.
Пусть звезда радиуса R испускает с единицы площади поверхности за единицу времени NL квантов, способных ионизовать атомы водорода. Число рекомбинаций пропорционально произведению концентраций свободных электронов ne и протонов np. Коэффициент пропорциональности обозначим через αt. Размерности двух новых величин есть
|
|
(1.34) |
Условие равенства числа ионизации и рекомбинаций есть
|
|
(1.35) |
Здесь предполагается сферичность зоны ионизации. Коэффициент рекомбинации зависит только от температуры, и поскольку температуры разных зон ионизации меняются мало, то αt , можно считать приблизительно постоянной. В области полной ионизации ne ≈ np. Поэтому
![$$
s_0 = \sqrt[3]{\frac{3R^2N_L}{\alpha_tn_e^2}} = \frac{U(Sp)}{n_e^{2/3}},
$$](https://images.astronet.ru/pubd/2013/03/01/0001281314/tex/formula132.gif)
|
(1.36) |
где U(Sp) есть некоторая величина, зависящая от спектрального типа звезд. Ее можно рассчитать теоретически на основе моделей атмосфер звезд, можно также определить и по данным наблюдений. Теоретические п наблюдательные значения U(Sp) достаточно близки.
Соотношения (1.36) следует рассматривать как условие подобия - у звезд одного и того же спектрального класса величины ![]() одинаковы. Это условие можно использовать для оценки s0 при известном ne и наоборот. Можно также оценить и массу газа внутри зоны Стремгрена:
одинаковы. Это условие можно использовать для оценки s0 при известном ne и наоборот. Можно также оценить и массу газа внутри зоны Стремгрена:
|
|
(1.37) |
где mp - масса протона. Подставляя сюда (1.36), находим
|
|
(1.38) |
Здесь критерий подобия заключается в том, что Msne есть постоянная величина для звезд данного спектрального класса. Любопытно, что Ms много больше массы звезд, например, у звезд класса O7 имеем U(Sp) = 62 пс см-2 Msne ≈ 104M☉ ⋅ 1 см-3 .
Мы здесь ограничимся только этими простыми примерами. В последующих главах будут многократно использованы методы анализа размерностей для получения различных соотношений между астрофизическими величинами. Много различных соотношений подобия будут использованы для объяснения наблюдаемых зависимостей.
Но, применяя методы теории размерностей и подобия, всегда нужно иметь в виду, что выбор исходных параметров определяется физикой явления, а отнюдь не одними соображениями размерности. Если при составлении списка определяющих параметров не будут учтены некоторые важные величины, то соображения анализа размерностей и подобия могут привести к ошибочным выводам.
И наконец последнее. Как неоднократно подчеркивалось, численное значение "значащих" безразмерных комплексов, являющихся к тому же и критериями подобия, из соображений размерностей не определяется. Но часто эти комплексы действительно мало отличаются от единицы. Это общее свойство можно объяснить и так. Если рассматриваемый объект находится в равновесном состоянии, то это означает, что примерно равны две противоположно действующие силы, например, сила тяготения и сила газового давления (в случае звезды), или сила кулоновского притяжения и квантового "шрёдингеровского давления", по определению Вайскопфа [13], при нахождении величин α0 и χH согласно (1.33). Безразмерный комплекс есть отношение величин этих сил, в случае их равенства в равновесном состоянии этот комплекс должен быть близок к единице.
<< § 1.3 Подобие и моделирование | Оглавление | § 1.5 Мировые (фундаментальные) постоянные >>