8.2 Аналитические и численные методы анализа радиального распределения пространственной звездной плотности в скоплениях
Мы знаем, что, как правило, скопления имеют эллиптическую форму. Простейшей гипотезой, которую мы можем принять в этом случае, будет гипотеза, согласно которой поверхности равной пространственной плотности являются подобными и подобно расположенными сфероидами. В проекции на плоскость они должны представляться подобными и подобно расположенными эллипсами. Мы знаем, что в действительности это не так. Но отклонения от этой картины обычно малы. Как правило, можно принимать для всего скопления некоторые средние параметры эллиптичности. Естественно, что вначале задачу перехода от видимого распределения звездной плотности F(r) в скоплении к распределению пространственной плотности f(r) решали для случая сферической симметрии распределения.
а) Аналитические методы.
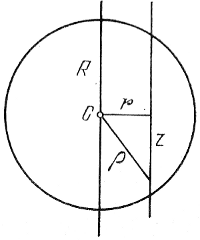
Рис. 117. Схема, поясняющая вывод формул (8.4) - (8.6).
На рис. 117 изображен разрез сферического скопления плоскостью, проходящей через глаз наблюдателя и центр скопления С, R - радиус скопления. Видимая плотность звезд на расстоянии r от центра скопления F(r), очевидно, связана с пространственной звездной плотностью f(r) соотношением
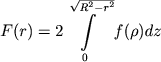
|
(8.4) |
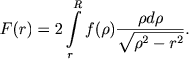
|
(8.5) |
Вначале Цейпель (1908) получил и опубликовал очень сложное для практического применения решение этого интегрального уравнения Абеля:
![$$
f(\rho) = \frac{1}{\pi}\int\limits_0^R \sqrt{\rho^2 - r^2} \frac{d}{dr} \left[\frac{F'(r)}{r}\right]dr.
$$](https://images.astronet.ru/pubd/2011/06/28/0001252610/tex/formula56.gif)
|
(8.6) |
Впоследствии Цейпель и Линдгрен (1921) нашли более простое выражение для определения f(r):
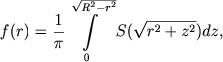
|
(8.7) |
|
|
(8.8) |
вывод которого можно найти в любом курсе звездной астрономии (см., например, Куликовский, 1978, с. 141 - 143). Так как в (8.7) входит производная F(r) по r , метод Цейпеля не требует при использовании кривой F(r) предварительного исправления ее за плотность звезд фона, считающуюся обычно постоянной.
Очень изящен метод Пламмера (1911); по сравнению с методом Цейпеля он исключительно прост и поэтому неоднократно применялся рядом авторов. На рис. 118 хСу - картинная плоскость, проходящая через центр скопления С . Ось z направлена к наблюдателю. Рассмотрим сечение скопления плоскостью y'Oz' , параллельной плоскости yCz и проходящей на расстоянии ОС = r от его центра. Обозначим через ρ и l расстояния любой из точек этого сечения от точек С и О соответственно.
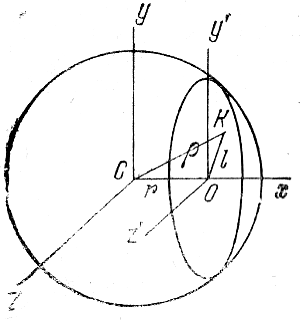
Рис. 118. Схема, поясняющая вывод формул (8.9) - (8.13).
Число звезд скопления, наблюдаемых в проекции на небесную сферу в полосе шириной dr , находящейся на расстоянии r от его центра, обозначим через Ф(r)dr . Очевидно,
|
|
(8.9) |
Переходя к полярным координатам в плоскости y'Oz', можем написать
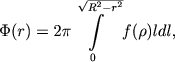
|
(8.10) |
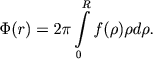
|
(8.11) |
Дифференцируя обе части равенства (8.11) по параметру r , находим
|
|
(8.12) |
|
|
(8.13) |
При пользовании этим методом на практике проекция скопления разбивается на ряд параллельных полос единичной ширины, подсчеты чисел звезд в которых (за вычетом соответствующих чисел звезд фона) дают Ф(r). Удобную для некоторых практических целей формулу, основанную на комбинации методов Цейпеля и Пламмера, предложил Курт (1969, с. 200):
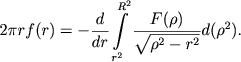
|
(8.14) |
Обобщения методов Цейпеля и Пламмера на случай эллипсоидального распределения плотности были предложены Кинле (1928) и Бруггенкате (1928). К сожалению, Кинле дал неверную формулу, а Бруггенкате - слишком частное решение, связывающее распределение пространственной плотности звезд в скоплении с распределением их видимой плотности вдоль малой оси эллипса проекции скопления.
Обобщение решений Цейпеля и Пламмера на случай, когда поверхности равной плотности в скоплении являются концентрическими, подобными и коаксиальными сфероидами, можно найти в работах Холопова (1949а, 1953б). Если η0 - отношение истинной малой полуоси сфероида (η0l) к большой (l), i - наклонение малой оси сфероида к лучу зрения, F(l) - видимая плотность в точках эллипса с большой полуосью l, a L- большая полуось сфероида, ограничивающего скопление, то пространственная плотность f(l) в точках сфероида с большой полуосью l
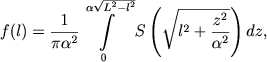
|
(8.15) |
При η0 = 1 формула (8.15) переходит в (8.7). Соответствующая формула, являющаяся обобщением формулы (8.13), имеет вид
|
|
(8.16) |
где значения Ф(l) определяются подсчетами звезд в полосах, параллельных малой оси эллипса проекции скопления на небесную сферу. Если ε - наблюдаемый эксцентриситет этого эллипса, то форма скопления определяется эксцентриситетом е его меридионального сечения
|
|
(8.17) |
Естественно, что при пользовании формулами (8.15) и (8.16) мы можем найти решение f(l) только как функцию i.
Так как е ≤ 1, из (8.17) вытекает, что существует предельный наименьший угол i0, определяемый равенством sin i0 = ε, при котором скопление обращается в диск. Поэтому практически можно получить несколько вариантов решения для разных значений i, лежащих в пределах от 90°; до i0. Реальный выбор i ограничивается тем, что мы не знаем ни одного скопления, для которого величина η была бы меньше 0,6, т. е. значение е превышало бы 0,8.
Для практического применения аналитические методы все же не очень удобны, так как требуют обращения к трудоемким операциям численного дифференцирования и интегрирования. Поэтому ряд авторов уже давно разрабатывал более простые численные методы решения задачи.
б) Численные методы. Первый из них был развит Парвулеско
(1925), который принял, что скопление состоит из n концентрических и взаимопроникающих сфер однородной плотности, убывающей по мере роста радиуса сферы (рис. 119). Эта система сфер в проекции на картинную плоскость образует ряд кольцевых областей, ограниченных радиусами ![]() , где R - радиус скопления. На рис. 119 изображены прямые, по которым плоскость чертежа, проходящая через центр скопления и глаз наблюдателя, пересекается касающимися сфер цилиндрами, оси которых параллельны лучу зрения.
, где R - радиус скопления. На рис. 119 изображены прямые, по которым плоскость чертежа, проходящая через центр скопления и глаз наблюдателя, пересекается касающимися сфер цилиндрами, оси которых параллельны лучу зрения.
Доля число звезд скопления, проектирующихся на внешнюю кольцевую область, на величину соответствующего объема, заключенного между поверхностью сферы с радиусом R и поверхностью цилиндра, касательного
к сфере с радиусом ![]() , можно сразу найти пространственную плотность самой большой сферы, f(R). Зная f(R), можно определить число звезд этой сферы, проектирующихся на следующую кольцевую область, и вычтя его из общего числа звезд, наблюдаемых в этой области, найти приходящегося на нее число звезд сферы с радиусом
, можно сразу найти пространственную плотность самой большой сферы, f(R). Зная f(R), можно определить число звезд этой сферы, проектирующихся на следующую кольцевую область, и вычтя его из общего числа звезд, наблюдаемых в этой области, найти приходящегося на нее число звезд сферы с радиусом ![]() , а затем и пространственную плотность звезд в этой сфере,
, а затем и пространственную плотность звезд в этой сфере, ![]() и т.д.
и т.д.
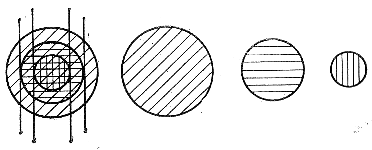
Рис. 119. Схема, поясняющая идею метода Парвулеско.
Для получения значения пространственной плотности на данном расстоянии от центра скопления остается просуммировать плотности f всех сфер, проектирующихся на соответствующую этому расстоянию кольцевую область.
Второй метод, по существу, являющийся модификацией предыдущего, был независимо предложен Валленквинстом (1933), который использовал вместо сфер сферические пояса одинаковой толщины с плотностью, возрастающей с приближением к центру, и дал удобную систему формул для последовательного определения f(r) в десяти сферических поясах, на которые разбивалось скопление, начиная с наружного пояса и кончая центральной сферой.
Позже Валленквист (1960) опубликовал аналогичный метод, в котором предусмотрено увеличение ширины поясов, на которые разбивается скопление, с увеличением расстояния от центра, что рационально, так как во внешних областях плотность меняется медленнее, чем в центре. В той же работе, по-видимому, для полноты разработки проблемы Валленквист предложил численный метод, основанный на проведении подсчетов звезд не в кольцах, а в параллельных полосах, - аналог аналитического метода Пламмера. Разобьем проекцию скопления на n колец одинаковой ширины и n параллельных полос, границы которых - касательные к соответствующим окружностям. Введем обозначения: rn - радиус скопления, rm - радиус m-го кольца (m < n), Nm - число звезд, наблюдаемых в m-й полосе (после учета фона), а fm - средняя пространственная плотность в пределах m-гo сферического пояса (ограниченного радиусами rm и rm-1). Тогда
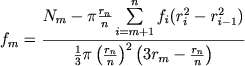
|
(8.18) |
В 1965 г. Кузмин и Велтманн (1972) применили методику Пламмера для нахождения распределения пространственной плотности звезд в шаровых скоплениях М 3 и М 15 путем фотоэлектрических наблюдений, сканируя скопление длинной узкой щелью (13",4 x 447") в направлении, перпендикулярном к длине щели. Простое дифференцирование потока излучения, поступающего от щели, позволяет получить, в соответствии с формулой (8.13), распределение пространственной плотности звезд в скоплении (см. также Кузмин и др., 1977).
Обобщение первого численного метода Валленквиста (1933) на случай, когда скопление является сфероидом, причем поверхности равной плотности в нем суть концентрические, подобные и подобно расположенные сфероиды, было предложено Холоповым (1949б), опубликовавшим систему формул для последовательного вычисления значений пространственной плотности fi в 25 сфероидальных поясах, на которые делится скопление, по значениям средней видимой плотности Fi, определяемым в соответствующих эллиптических кольцах, ограниченных эллипсами постоянной видимой плотности.
Если обозначить через am большую полуось m-го сфероида (считая, что am-1 < am), то
![$$
\begin{array}{ll}
f_m &=\frac{3}{4}aF_m(a_m^2 - a_{m-1}^2)^{-1/2} - (a_m^2 - a_{m-1}^2)^{-3/2} \times \\
&\times\sum\limits_{i=m+1}^{n} f_i \Bigl((a_i^2 - a_{m-1}^2)^{3/2} - (a_i^2 - a_m^2)^{3/2} - \\
&-[(a_{i-1}^2 - a_{m-1}^2)^{3/2} - (a_{i-1}^2 - a_m^2)^{3/2}]\Bigl)
\end{array}
$$](https://images.astronet.ru/pubd/2011/06/28/0001252610/tex/formula74.gif)
|
(8.19) |
|
|
(8.20) |
i - угол между осью вращения скопления и лучом зрения, η - отношение видимой малой оси эллипса проекции скопления к большой, η0 - отношение истинной малой оси скопления к большой. Система формул (8.19), где n = 1, 2, ..., n, отличается от системы формул Валленквиста (1933) лишь наличием множителя а в первом члене каждой формулы.
При вычислении Коэффициентов системы (8.19) удобнее всегопринять за единицу длины 1/n большой полуоси внешнего сфероида, выражая в этих единицах Fm и fm и считая, что а1 = 1, а2 = 2, ..., аn = n. Чем больше n, тем точнее будут получаемые значения fm. Валленквист (1933) вычислил значения коэффициентов своей системы при n = 10, Холопов (1949б) - при n = 25. В последнем случае система формул (8.19) имеет вид
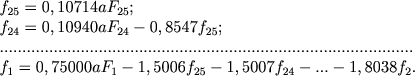
|
(8.21) |
Мы не приводим ее полностью, так как при использовании ЭВМ проще предоставить самой машине вычисление коэффициентов по формуле (8.19), чем вводить в ее память массив, содержащий 325 известных чисел.
При η = 1 и n = 10 из формул (8.21), как частный случай, получаются формулы Валленквиста (1933) путем простого отбрасывания лишних слагаемых с индексами, большими 10. Вообще, как видно из (8.19), можно разбить скопление на любое число поясов l ≤ n и пользоваться полученными формулами (8.19) или (8.21), отбросив все члены с индексами, бóльшими l, т. е. просто считая, что при i > 1 все fi = 0.
Система (8.21) показывает также, что для ее решения при а ≠ 1 можно сначала решить ее при условии, что а = 1, а затем лишь умножить все полученные значения fm на а. Таким образом, форма кривой f(l) не зависит от величины неизвестного нам угла i между осью симметрии системы и лучом зрения: умножение всех значений fm на а сводится к изменению числа звезд в рассматриваемой группе, что эквивалентно растяжению или сжатию кривой f(l) по оси ординат без изменения ее формы.
Кроме того, нетрудно видеть, что система (8.21) применима и для случая, когда скопление является вытянутым эллипсоидом вращения (Холопов, 1953в). Единственная разница при обработке состоит в том, что за экваториальную полуось при этом принимается малая полуось эллипса проекции скопления, а η оказывается больше 1. Таким образом, форма кривой f(l) не зависит и от того, является ли эллипсоид вращения в действительности сплюснутым или вытянутым. Особенности функции распределения пространственной плотности звезд в скоплении f(l) в рассмотренном приближении определяются лишь особенностями функции распределения их видимой плотности F(l).
Система (8.21) чрезвычайно удобна и в том отношении, что с ее помощью можно, зная распределение f(l) во внешних областях скопления, учитывать влияние этих областей на распределение F(l) во внутренних областях. Для этого достаточно во всех формулах, содержащих, например, Fi с i ≤ m, приравнять нулю значения fi с i ≤ m и вычислить затем соответствующие значения Fi по известным для i > m значениям fi.
Для точного вычисления f(r) во внешних областях скоплений больших угловых размеров (R > 5°;), каким являются, например, Гиады, уже нельзя пренебрегать непараллельностью прямых, соединяющих глаз наблюдателя с границами поверхностей равной плотности в этих системах. В этом случае упомянутые прямые являются образующими уже не цилиндрических, а конических поверхностей. Соответствующие системы формул численного метода для определения пространственной плотности в сферических системах, угловые радиусы которых достигают 15, 30, 60 и 90 градусов, по распределению видимой плотности их членов опубликовал Налимов (1967).
Метод решения уравнения (8.5), позволяющий судить о точности определения функции f(r), предложил Косарев (1973).
<< 8.1 Видимое распределение звезд в скоплениях. Методы анализа отклонений формы шаровых скоплений от сферической | Оглавление | 8.3 Методика построения кривых изменения видимой плотности F(r) >>
|
Публикации с ключевыми словами:
звезды - Скопление
Публикации со словами: звезды - Скопление | |
См. также:
Все публикации на ту же тему >> | |