5.1 Происхождение "комбинационных спектров"
Рассмотрим оболочку, окружающую горячую звезду, причем будем предполагать, что оболочка движется. Для начала применим к этой оболочке результаты, полученные нами в предыдущей главе.
Мы вычислим и сравним между собою следующие величины: 1) энергию, излучаемую звездой в непрерывном спектре, 2) энергию, излучаемую оболочкой в непрерывном спектре, и 3) энергию, излучаемую оболочкой в спектральных линиях. Эти вычисления будут относиться к водородной оболочке.
Если оболочка прозрачна для излучения в субординатных сериях и поглощает только излучение от звезды за границей основной серии, то, как известно, непрерывный спектр оболочки в видимой части будет очень слаб по сравнению с непрерывным спектром звезды. Вместе с тем яркие линии будут весьма сильны на фоне непрерывного спектра оболочки. Такое положение имеет место в газовых туманностях. Иначе обстоит дело в оболочках малого радиуса. Эти оболочки поглощают излучение, идущее от звезды не только за границей основных серий, но и за границами субординатных серий. Благодаря этому интенсивность непрерывного спектра оболочек сильно возрастает. Интенсивность же ярких линий не испытывает при этом столь сильного возрастания из-за непрозрачности оболочки для излучения в линиях. Поэтому при значительной непрозрачности оболочки для: излучения в линиях (точнее говоря, при малых значениям введенного ранее параметра x) следует ожидать весьма сильного непрерывного спектра оболочки по сравнению с непрерывным спектром звезды при сравнительной слабости ярких линий. Мы проверим сейчас эти соображения непосредственными вычислениями.
Пусть Еν∗ есть энергия, излучаемая в частоте ν звездой, и Eν - энергия, излучаемая в частоте v оболочкой. Эти величины определяются формулами
|
|
(1) |
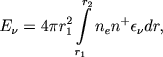
|
(2) |
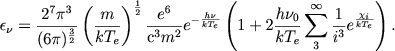
|
(3) |
В формуле (3) первый член в скобках учитывает free-free transitions, второй - free-baund transitions. Суммирование ведется начиная с i=3, так как величину Eν, мы предполагаем вычислить для видимой части спектра. Пусть далее Ek2 есть полная энергия, излучаемая оболочкой в бальмеровской линии, соответствующей переходу k → 2. Эта величина равна
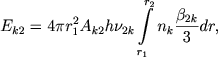
|
(4) |
где β2k/3 есть доля квантов, уходящих из оболочки в данной линии вследствие эффекта Доплера.
Для вычисления интегралов (4) и (4) мы воспользуемся формулами, определяющими степень возбуждения и ионизации в оболочке, выведенными в предыдущей главе. Эти формулы имеют вид
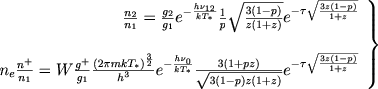
|
(5) |
где величина z связана с параметром x соотношением
|
|
(6) |
|
|
(7) |
Напомним, что при выводе формул (5) величина z считалась постоянной в оболочке.
Вместо соотношения (2) можно написать
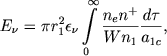
|
(8) |
где τ - оптическая глубина за границей основной серии. Подставляя в (8) вторую из формул (5), получаем
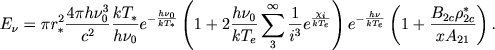
|
(9) |
Отсюда видно, что величина Eν сильно возрастает с уменьшением параметра х.
Для вычисления интеграла (4) необходимо разбить его на два интеграла: по области, непрозрачной для излучения в данной линии, и по области, прозрачной для этого излучения. Выполняя это, для Ek2 находим
![$$
E_{k2} = 4\pi r_1^2 A_{k2} h\nu_{2k} \left[\int\limits_{0}^{\tau_1} n_k \frac{\beta_{2k}}{3} \frac{d\tau}{a_{1c}} + \int\limits_{\tau_1}^\infty n_k \frac{d\tau}{a_{1c}} \right].
$$](https://images.astronet.ru/pubd/2011/06/28/0001252608/tex/formula158.gif)
|
(10) |
Эту формулу можно преобразовать к виду
![$$
E_{k2} = \pi r_*^2 A_{k2} h\nu_{2k} \left[\frac{n_k}{n_2} x \frac{a_{12}}{a_{2k}} \int\limits_{0}^{\tau_1} \frac{d\tau}{a_{1c}} + \frac{n_k}{n_e n^+} \int\limits_{\tau_1}^\infty \frac{n_e n^+}{Wn_1} \frac{d\tau}{a_{1c}} \right].
$$](https://images.astronet.ru/pubd/2011/06/28/0001252608/tex/formula159.gif)
|
(11) |
Интегрируя и пользуясь тем, что при τ = τ1 должно быть
|
|
(12) |
вместо (1) получаем
![$$
E_{k2} = \pi r_*^2 \frac{A_{k2} h\nu_{2k}}{a_{1c}} \frac{n_k}{n_2} x \frac{a_{12}}{a_{2k}} \left[\tau_1 + \sqrt{\frac{1+z}{3(1-p)z}}\right].
$$](https://images.astronet.ru/pubd/2011/06/28/0001252608/tex/formula161.gif)
|
(13) |
Входящая в эту формулу величина τ1, т. е. граничное значение между двумя упомянутыми областями, определяется соотношением (12). С помощью первой из формул (5) из этого соотношения находим
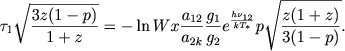
|
(14) |
Подставляя (14) в (13), окончательно получаем
![$$
E_{k2} = \left[ -\ln W x \frac{a_{12}}{a_{2k}} \frac{g_1}{g_2} e^{\frac{h\nu_{12}}{kT_*}} p \sqrt{\frac{z(1+z)}{3(1-p)}} +1 \right] \pi r_*^2 \frac{A_{k2} h\nu_{2k}}{a_{1c}} \frac{n_k}{n_2} x \frac{a_{12}}{a_{2k}} \sqrt{\frac{1+z}{3(1-p)z}} .
$$](https://images.astronet.ru/pubd/2011/06/28/0001252608/tex/formula163.gif)
|
(15) |
Этой формулой мы и будем пользоваться для вычисления полной энергии, излучаемой оболочкой в данной линии.
Сравним теперь между собою только что определенные величины E*ν, Eν и Ek2 Для характеристики отношения энергии в линии к энергии, излучаемой оболочкой в непрерывном спектре, мы воспользуемся занстровскими величинами Ak, равными
|
|
(16) |
С помощью вышеприведенных формул (1), (9) и (15) мы составили таблицы XIV и XV, в которых для разных значений параметра х даны значения величин Aβ и Eν/E*ν в облсти линии Hβ. Первая из этих таблиц относится к случаю T∗=20000°; ,Te=20000°;, вторая к случаю (T∗=50000°; ,Te=20000°;). Необходимые для вычислений значения величин n4/n2 были взяты из таблиц II и III главы I. Для W было принято значение W=10-4. Четвертая строчка каждой из таблиц дает отношение энергии, излучаемой в линии Hβ непрозрачной частью оболочки, к энергии, излучаемой и той же линии прозрачной частью оболочки. В пятой строчке даны значения оптической толщины оболочки за границей бальмеровской серии. Эта величина вычислялась по формуле
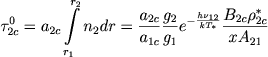
|
(17) |
(об этой величине см. ниже).
Таблица XIV
(T∗=20000°; ,Te=20000°;)
| x | 0,01 | 0,001 | 0,0001 |
| Eν/E∗ν | 0,03 | 0,24 | 2,1 |
| Aβ | 0,42 | 0,03 | 0,002 |
| 10 | 14 | 17 | |
| τ2c0 | 0,06 | 0,6 | 6,0 |
Таблица XV
(T∗=50000°; ,Te=20000°;)
| x | 1 | 0,1 | 0,01 |
| Eν/E∗ν | 0,6 | 1,6 | 11,5 |
| Aβ | 0,35 | 0,045 | 0,002 |
| 7 | 7 | 7 | |
| τ2c0 | 0,16 | 1,6 | 16 |
Из рассмотрения приведенных таблиц мы можем сделать следующий вывод. С уменьшением параметра х величина Eν/E∗ν возрастает, а величина Aβ убывает. При достаточно малых значениях х непрерывный спектр оболочки становится ярче непрерывного спектра звезды, а величина Aβ становится близкой к своим наблюдаемым в звездных спектрах значениям (порядка 0,001).
Из общих физических принципов следует, что излучение оболочки в непрерывном спектре должно соответствовать температуре более низкой, чем температура звезды. Это видно и из формулы (9), дающей распределение энергии в непрерывном спектре оболочки. Найдем, например, цветовую температуру оболочки в видимой части спектра. Из формулы (9) вытекает, что
|
|
(18) |
Обычно же считается, что распределение энергии в непрерывном спектре описывается формулой Планка с некоторой температурой Т'
|
|
(19) |
Легко видеть, что температуры Т' и Тe связаны друг с другом соотношением
|
|
(20) |
В области линии Hβ вместо (20) имеем
|
|
(21) |
Это значит, что температура Т' гораздо меньше температуры Тe. Так, например, при Тe = 20000°; для Т' получаем Т' = 6700°; . Поэтому излучение оболочки даже при очень высокой температуре Тe будет казаться низкотемпературным.
Отметим, что распределение энергии в спектрах звезд поздних классов с яркими линиями из-за сложного абсорбционного спектра известно плохо. Для звезды Z Andromedae Plaskett получил Т' = 5200°; ± 900°; . Несомненно, однако, что цветовые температуры долгопериодических переменных значительно ниже приведенного значения, ибо эти звезды весьма "красные".
Для объяснения сильного покраснения оболочки по сравнению с звездой следует иметь в виду, что наши результаты, приведенные выше, не вполне правильны. Дело в том, что при выводе формул (5), определяющих возбуждение и ионизацию в оболочке, мы считали, что оптическая толщина оболочки за границами субординатных серий меньше единицы. На самом деле, как видно из таблиц XIV и XV, с уменьшением параметра х величина τ2c0 возрастает и при достаточно малых значениях х становится τ2c0 > 1. В этом последнем случае теория лучевого равновесия делается весьма сложной, и подробное рассмотрение этого случая выходит за рамки настоящей работы. Однако вполне очевидным является следующее. Если τ1c0 >> 1, но τ2c0 < 1, то оболочка полностью поглощает излучение звезды за границей основной серии, частично поглощает излучение звезды за границами субординатных серий и излучает энергию за границами субординатных серий и в спектральных линиях. Кванты же за границей основной серии, излученные оболочкой, снова поглощаются в оболочке, и это продолжается до тех пор, пока почти все эти кванты не будут переработаны в кванты более низких частот. Этот случай был рассмотрен выше и привел к формуле (9), определяющей излучение оболочки в непрерывном спектре. Если же только τ1c0 >> 1, но и τ2c0 > 1, то оболочка перерабатывает в излучение низких частот не только излучение за границей основной серии, но и излучение за границами субординатных серий. Само собою разумеется, что это относится как к излучению, идущему от звезды, так и к собственному излучению оболочки. Ясно, что излучение оболочки во втором случае будет соответствовать еще более низкой температуре, чем в первом. Таково в общих чертах происхождение непрерывного спектра позднего типа, излучаемого оболочкой.
Как было выяснено выше, вид спектра оболочки существенно зависит от параметра х, равного
|
|
(22) |
Согласно же ионизационной формуле, Wn1 ∼ nen+. Это значит, что параметр х тем меньше, чем больше плотность оболочки. Поэтому мы приходим к заключению, что при прочих равных условиях (т. е. при одинаковых значениях температуры центральной звезды, коэффициента дилюции и т. д.) непрерывный спектр оболочки будет тем более поздним, чем больше плотность оболочки.
Нам еще остается объяснить происхождение абсорбционного спектра позднего типа. Для этого обратимся к положению дел во внешних частях оболочки. При достаточно малых значениях параметра х внутренняя, часть оболочки полностью экранирует высокочастотное излучение, идущее от звезды. Поэтому внешняя часть оболочки находится под воздействием низкотемпературного излучения самой оболочки. Следовательно, в этих частях возбуждение и ионизация атомов должны соответствовать весьма низкой температуре. Другими словами, здесь должны существовать неионизованные атомы металлов и молекулярные соединения. Именно во внешних частях оболочки и возникает абсорбционный спектр позднего типа.
Таким образом мы приходим к следующему выводу. Внутренняя часть оболочки играет роль "фотосферы", создавая непрерывный спектр позднего типа. Во внешней части оболочки, играющей роль "атмосферы", возникают абсорбционные линии неионизованных металлов и молекулярные полосы. В слое, непосредственно прилегающем к "фотосфере", возникают эмиссионные линии водорода и ионизованных металлов. При достаточно высокой температуре звезды в спектре должны наблюдаться также эмиссионные линии атомов с очень высоким потенциалом ионизации.
Следует подчеркнуть, что для наших выводов существенно, чтобы оптическая толщина оболочки за границами субординатных серий была больше единицы. Поэтому мы должны подробно рассмотреть причины, влияющие на величину τ2c0. Этому вопросу посвящается следующий параграф.
<< Глава V. Звезды поздних спектральных классов с яркими линиями | Оглавление | 5.2 Оптическая толщина оболочки за границами субординатных серий >>
|
Публикации с ключевыми словами:
оболочки звезд - перенос излучения
Публикации со словами: оболочки звезд - перенос излучения | |
|
См. также:
| |