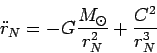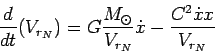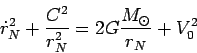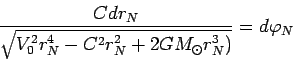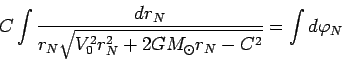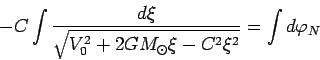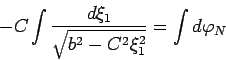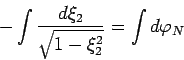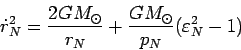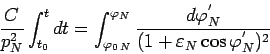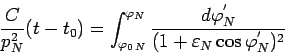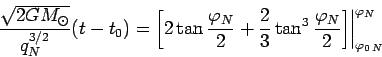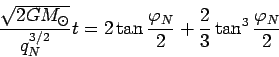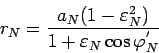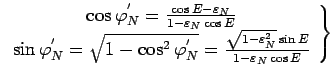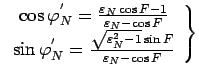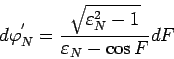<< C. Вычисление интегралов | Оглавление | Литература >>
D. Аналитическое решение для уравнений движения ядра кометы
В данном приложении будет рассмотрена задача о поиске
аналитического решения для уравнений движения ядра кометы (первая
пара системы (50)). Рассмотрим второе
уравнение системы (50)
Произведем замену переменных вида
![]() . Тогда
(78) можно переписать в виде:
. Тогда
(78) можно переписать в виде:
| (79) |
| (80) |
здесь
Следовательно, первое уравнение системы
(50) можно представить в виде:
Здесь учтено, что
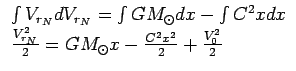 |
Откуда
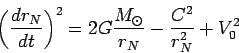 |
(84) |
где ![]() - постоянная интегрирования. Учтем также, что
- постоянная интегрирования. Учтем также, что
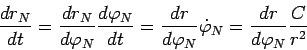
следовательно
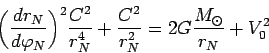
откуда
Проинтегрируем (87)
Произведем замену переменных вида ![]() , тогда
, тогда
![]() , следовательно (88) можно
представить в виде:
, следовательно (88) можно
представить в виде:
следовательно, (89) можно представить в виде:
произведем в (91) замену следующего вида
откуда получаем
Вернемся к исходной переменной
где
где
учитывая определение большой полуоси орбиты ядра
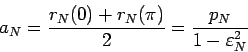 |
(97) |
Подставляя
Ситуация 1: Параболическая орбита
(
![]() ).
).
Тогда после интегрирования в правой части (101) и
учитывая, что ![]() , где
, где ![]() - перигелийное расстояние
ядра, будем иметь:
- перигелийное расстояние
ядра, будем иметь:
Решая последнее уравнение относительно
Ситуация 2: Эллиптическая орбита
(
![]() ).
).
В данном случае непосредственное интегрирование (101)
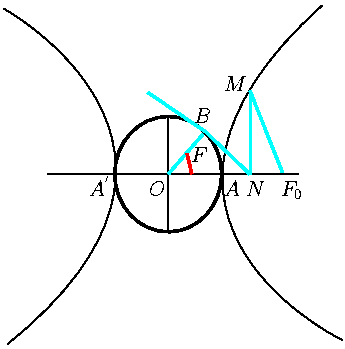
затруднительно. В этом случае удобно ввести вспомогательный угол
![]() - эксцентрическую аномалию и выразить
- эксцентрическую аномалию и выразить ![]() ,
, ![]() в
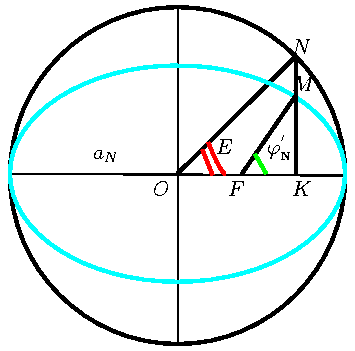
функции этого угла (смотри рис. 27).
в
функции этого угла (смотри рис. 27).
На большой оси как на диаметре строим окружность. Проводим через
положение ядра кометы (точка ![]() ) перпендикуляр
) перпендикуляр ![]() к большой оси
орбиты до пересечения с окружностью. Угол
к большой оси
орбиты до пересечения с окружностью. Угол ![]() и есть
эксцентрическая аномалия
и есть
эксцентрическая аномалия ![]() . Очевидно, что
. Очевидно, что ![]() или
или
или
Подставляя значение
Исключая из (105) и (106) переменную
(перед корнем берем знак "+", поскольку
Подставим значение
Решая последнее уравнение относительно переменной
Ситуация 3: Гиперболическая
орбита (
![]() ).
).
В случае гиперболической орбиты ядра кометы
![]() ,
,
![]() , а
, а
Для интегрирования (101) введем вспомогательный угол
Из ![]() проводим касательную к окружности и через точку касания
проводим касательную к окружности и через точку касания ![]() проводим прямую
проводим прямую ![]() ; угол
; угол ![]() . Имеем
. Имеем ![]() или
или
Используя (111), получаем окончательно
на основании (114) имеем
Подставляя значение
и производя замену следующего вида
получаем окончательно
Решая последнее уравнение относительно переменной
Таким образом, имея элементы орбиты кометы, можно всегда определить ее закон движения.
<< C. Вычисление интегралов | Оглавление | Литература >>
|
Публикации с ключевыми словами:
кометы - космическая пыль
Публикации со словами: кометы - космическая пыль | |
См. также:
Все публикации на ту же тему >> | |