<< 4. От Ньютона до Джинса | Оглавление | 6. Какие звёзды рождаются >>

От Джинса до наших дней

"...разумно надеяться, что в не слишком отдаленном будущем мы сможем понять такую простую вещь, как звезда." [24] А. Эддингтон, 1926 г. "...чем больше мы познаем действительное состояние такого сложного физического образования, каким является звезда, тем более запутанным оно нам представляется." [32] М. Шварцшильд, 1960 г.

Джеймс Хопвуд Джинс (рис. 5.1), только что блестяще закончивший Кембриджский университет, в течение нескольких лет выполняет серию выдающихся работ по разным разделам теоретической физики: он публикует монографию по кинетической теории газов, исследования по молекулярной физике и теории излучения [33]. В начале 1900-х годов под влиянием профессора астрономии и физики Кембриджского университета Джорджа Говарда Дарвина (сына знаменитого биолога Чарлза Дарвина) Джеймс Джинс выполняет серию работ по теоретической астрофизике. Среди них была и фундаментальная работа "Устойчивость сферической туманности", опубликованная в 1902 г. в "Сообщениях Лондонского королевского общества". Джеймсу в ту пору было 25 лет. Эта работа о поведении газовых уплотнений под действием силы самогравитации стала фундаментом современной теории гравитационной неустойчивости, объясняющей происхождение практически всех структурных элементов Вселенной - от галактик и их скоплений, до звезд, планет и их спутников. Характерные размер и масса гравитационно-неустойчивых газовых уплотнений называются с тех пор джинсовскими и отмечаются индексом J (от James Jeans), например, M_J - джинсовская масса, R_J - джинсовский .радиус.

Вообще, Дж. Дарвин мог гордиться тем, что привлек внимание молодого Джинса к астрономии: его подопечный сделал очень многое для развития космогонии и звездной динамики.

Рис. 5.1. Джеймс Хопвуд Джинс - создатель теории гравитационной неустойчивости. Этот портрет находится в галерее Лондонского королевского общества, членом, а затем и секретарем которого долгие годы был выдающийся ученый

Но мог ли предполагать Дж. Дарвин, занимавший в 1899-1900 гг. пост президента Королевского астрономического общества, что через четверть века на эту почетную должность вступит Дж. Джинc и в память о своем наставнике учредит ежегодные Дарвиновские лекции. Впрочем, связь между Дарвиным и Джинсом оказалась еще более глубокой. Дарвин прославился изучением приливов и фигур вращающихся жидких тел [29]. Джинс продолжил исследования космогонической роли приливных явлений и даже разработал приливную теорию происхождения Солнечной системы, очень модную в первой половине XX века. В этой теории рождение планетной системы рассматривается как редчайший факт, вызванный близким пролетом рядом с Солнцем другой звезды, вырвавшей из оболочки Солнца сгусток прото-планетного вещества [34]. И хотя в отношении Солнечной системы эту гипотезу вспоминают сейчас лишь как исторический факт, сам механизм приливного взаимодействия несомненно играет большую роль в мире галактик, звездных скоплений и, возможно, протозвезд [35].

Вернемся, однако, к теории гравитационной неустойчивости. После того, как в начале XX века Дж. Джинс заложил ее фундамент, астрономам понадобилось еще 70 лет для обнаружения именно того компонента межзвездной среды, который непосредственно связан с формированием звезд и при описании которого теория Джинса правильно предсказывает массы и размер новорожденных звезд. Давайте кратко познакомимся с этой теорией.

Ньютон, развивая идею гравитационной конденсации первичного вещества, предполагал это вещество совершенно инертным, холодным, не сопротивляющимся гравитации. Поэтому он считал, что любая неоднородность плотности должна прогрессивно сжиматься и уплотняться силой тяжести. К концу XIX века физики уже ясно понимали, что всякое вещество, в том числе и разреженный газ, обладает упругостью: именно это свойство газа позволяет распространяться в нем звуковым волнам. Поэтому Джинс заключил, что процесс гравитационного сжатия может начаться лишь в том случае, если сила тяжести победит силу газового давления.

Обычно, чтобы описать распространение звука в газе, физики записывают уравнение колебаний, в которое входят инерционные характеристики газа (плотность, масса молекул) и силовые (давление). Джине впервые добавил в это уравнение новый член, учитывающий гравитационное взаимодействие частиц газа. Оказалось, что при этом уравнение получило новые решения; при высокой частоте колебаний, т. е. при малой длине волны, его решением по-прежнему оставались бегущие или стоячие звуковые волны, но чем больше становится длина волны, тем сильнее чувствуется влияние гравитации, и, наконец, при определенной критической длине волны l_J распространение звуковых волн прекращается. Все уплотнения в газе, характерный размер которых превышает l_J, должны неудержимо сжиматься под действием собственной силы тяжести - газовое давление не может противостоять этому.

Объяснить это явление можно довольно просто. Рассмотрим, какие процессы происходят при небольшом случайном сжатии облака газа с характерным размером l и плотностью r. С одной стороны, сила гравитации стремится продолжить это сжатие. Если бы газовое давление вообще отсутствовало, то все вещество упало бы к центру облака за время свободного падения (free fall time):

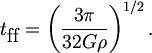
(5.1)

Это выражение легко можно получить из Третьего закона Кеплера: время полуоборота по очень вытянутой эллиптической орбите, т. е. время свободного падения, равно p(l³/GM)^1/2, а масса облака М = 4pl³r/3.

С другой стороны, в случае отсутствия гравитации силы газового давления заставили бы облако расшириться за динамическое (dynamic), время: t_dyn = l/V_s, где V_s - скорость звука, которая зависит только от температуры и химического состава газа. Если возмущения плотности в газе слабы (т. е. r » r₀ и Т » T₀), то отношение t_dyn / t_ff ~ l. Значит, в возмущениях плотности маленького размера (t_dyn << t_ff) газовое давление всегда будет успевать перераспределить вещество таким образом, чтобы воспрепятствовать дальнейшему сжатию. И напротив, возмущения плотности большого размера (t_dyn >> t_ff), случайно возникнув, уже не смогут вновь расшириться: у них для этого просто не хватит времени, так как гравитация сработает быстрее, чем сила газового давления.

Каковы же критические значения l_J и М_J? Грубо их можно оценить, приравняв друг другу t_ff и t_dyn, а более точно - из условия равновесия газа под действием давления и силы тяжести. Звуковая волна - это циклический процесс сжатия и разрежения газа: полпериода длится сжатие, полпериода - разрежение. Значит, характерный размер области уплотнения l/2, а ее масса М = r(l/2)³. Известно, что давление идеального газа Р = RTr/m, где R = 8,31 10³ Дж/К кг - универсальная газовая постоянная, а Т и m - температура и молекулярный вес газа. Очевидно, выталкивающая сила, действующая на единичный объем газа, в первом приближении равна P/(l/4), а сила тяготения, стремящаяся погрузить элемент объема газа внутрь возмущения плотности, может быть записана так: GMr/(l/4)². Длина волны и масса возмущения становятся критическими, когда эти силы равны: 4P/l_J = GM_Jr/(l_J/4)². Отсюда:

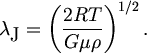
(5.2)

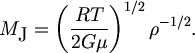
(5.3)

Последняя формула является важнейшей в теории гравитационной неустойчивости Джинса. Из нее следует, что если в покоящейся разреженной среде в силу каких-то причин возникают возмущения плотности различного масштаба, то те из них, масса которых М > M_J, должны неудержимо сжиматься и уплотняться. Обычно в газе возмущения плотности малых масштабов преобладают над крупномасштабными, поэтому наиболее вероятно, что гравитационной неустойчивости подвергнутся возмущения с массой М » М_J.

Спустя 240 лет после письма Ньютона к Бентли Джине написал в своей книге "Звезды в их развитии" (в русском переводе - "Движение миров" [36]): "Предположим, что в начале времен все пространство было заполнено газом... Тогда можно доказать, что газ не оставался бы равномерно распределенным в пространстве, а немедленно стал бы собираться в шары. Мы можем вычислить, сколько газа потребуется для образования каждого шара". К сожалению, Джинс немного преувеличивал свои возможности: он не мог достаточно убедительно проверить работоспособность своих формул, так как в то время почти ничего не было известно о физических свойствах и составе межзвездного газа, из которого формируются звезды. Однако теперь мы можем это сделать.

Химический состав звезд и межзвездного газа отличается большой стабильностью: на 1000 атомов водорода приходится около 100 атомов гелия и 2-3 атома более тяжелых элементов. В плотных холодных облаках, в которых формируются звезды, водород находится в форме молекул Н₂, молекулярный вес которых m(Н₂) = 2. С учетом всех других химических элементов средний молекулярный вес газа в облаках составляет m = 2.3. Используя это значение, удобно нормировать формулу (5.3) на характерные параметры межзвездного газа:

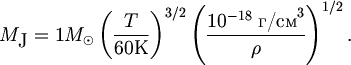
(5.4)

Как мы увидим далее, типичными местами формирования звезд являются мелкомасштабные конденсации в молекулярных облаках, где температура Т = (5 - 20) К и плотность Т = (10^-20 - 10^-18) г/см³. Подставив эти значения в формулу Джинса, мы определим, что M_J = (0.02 - 2) M. Действительно, массы большинства звезд заключены именно в этом диапазоне - убедительный аргумент в пользу теории гравитационной неустойчивости. Еще одним тестом для этой теории может служить размер облака - предка звезды. Для Солнечной системы этот размер из наблюдений оценивается в 10⁴ а. е.: именно в этом объеме сосредоточена основная масса ядер комет (так называемое, внутреннее облако Оорта). А что предсказывает на этот счет теория Джинса?

Радиусом газового фрагмента в момент наступления его гравитационной неустойчивости естественно считать величину R_J = l_J/4, значение которой

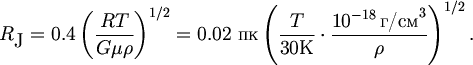
(5.5)

В последние годы, говоря о плотности межзвездной среды, астрономы все чаще используют не массовую плотность r, а концентрацию молекул водорода n(H₂). Поэтому формулы (5.4) и (5.5) можно переписать в более удобной форме, используя очевидное соотношение

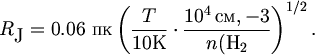
(5.6)

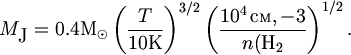
(5.7)

Для типичных параметров газа в областях звездообразования - Т = 20 К и n(H₂) = 10⁴ см^-3, - приводящих к значению M_J = 1.4 M, теория предсказывает критический радиус облака R_J = 0.08 пк » 10⁴ а. е. Такое хорошее совпадение значения R_J и наблюдаемого размера Солнечной системы также является впечатляющим свидетельством в пользу теории Джинса.

Разумеется, простые формулы Джинса не учитывают многих физических процессов, происходящих в межзвездной среде. Эти формулы верны для идеального покоящегося однородного газа, который в природе никогда не встретишь. Межзвездное вещество находится в постоянном движении со скоростью, часто превосходящей скорость звука; оно испытывает сильное влияние магнитного поля, притяжение к звездам Галактики и лучевое давление со стороны наиболее ярких из них. Поэтому многие физики после Джинса брались за уточнение и развитие теории гравитационной неустойчивости. Отметим среди них Е.М. Лифшица, С. Чандрасекара, Я.Б. Зельдовича, Дж. Силка. Сейчас эта теория развита вполне детально: она учитывает расширение и вращение газовой среды, ее взаимодействие с магнитным полем и с другими источниками гравитации. Тем, кто захочет познакомиться с ее математическим аппаратом и основными приложениями, советуем воспользоваться книгами [37-40].

Важно, однако, что учет дополнительных физических факторов принципиально не изменил выводы теории: значения джинсовской массы и джинсовского радиуса, определенные формулами (5.6) и (5.7), до сих пор используются в большинстве работ при оценке результатов гравитационной неустойчивости. Отчасти это связано с тем, что из наблюдений редко удается получить иные характеристики протозвездной среды, кроме ее плотности и температуры.

Сам Джинс был чрезвычайно воодушевлен результатом своих исследований и прежде всего их наглядностью и простотой. Он писал: "...для нас ясно, почему все звезды имеют очень сходный вес; это потому, что все они образованы одинаковым процессом. Они, пожалуй, похожи на фабричные изделия, сделанные одною и тою же машиной" [36]. Зная сегодня, что звезды различаются по массе в тысячи раз, а условия в межзвездной среде - еще сильнее, мы вправе назвать оптимизм Джинса преждевременным. Однако он и сам понимал, что пройден лишь первый рубеж, и, предвидя грядущие трудности, с которыми столкнется теория формирования звезд и галактик, заключил: "При современном состоянии ваших знаний любая попытка диктовать окончательные решения по основным проблемам космогонии была бы ничем иным, как чистым догматизмом".

---

<< 4. От Ньютона до Джинса | Оглавление | 6. Какие звёзды рождаются >>

Публикации с ключевыми словами: Протозвезды - звездообразование Публикации со словами: Протозвезды - звездообразование
См. также: NGC 604: гигантские звездные ясли NGC 7714: вспышка звездообразования после столкновения галактик Туманность Конус от телескопа имени Хаббла NGC 1893 и Головастики в IC 410 Звездообразование в туманности Пакман Звезды, пыль и туманность в NGC 6559 NGC 1333: звездные ясли в Персее Все публикации на ту же тему >>