<< 2. On a New Wave Crest | Contents | Afterword >>

---

III. THE LIN-SHU THEORY

I would like to acknowledge that Professors Lin and Toomre of MIT are also interested in the problem of spiral structure, and that I have benefited from discussions with them as well as their students.

Kalnajs 1963, p.13

3.1 Working hypothesis and semi-empirical theory

In hindsight, considering the crucial influence that the Lin & Shu (1964) paper had on the thinking of astronomers, it is only regretful that Lin did not decide (with or without me) to publish even earlier, because he certainly had all the physical ideas contained in our paper well before 1964.

Shu 2001

While Toomre, Hunter and Kalnajs had already presented their first results in the dynamics of flat galaxies, Lin still kept on thinking over the spiral problem. ⁶³ Astronomers in Princeton had convinced him that, despite Chandrasekhar's criticism of Lindblad's theories, ⁶⁴ the idea itself of a long-lived, shape-preserving spiral pattern is consistent with Hubble's classification system that relates spiral features with a galaxy's morphological type, its steady characteristic, thus suggesting that the spirals are steady as well. This view reminded Lin of wave modes in fluid flows that he had been studying for years back. ⁶⁵ On purely heuristic grounds, discrete spiral modes seemed to him very reasonable as the natural result of wave evolution, and, if so, the patterns released might be associated with slowly growing or neutral modes. Lin raised this premise to the rank of working hypothesis, and around it as the nucleus he set to develop a semi-empirical theory. ⁶⁶ It was seen to follow best the "urgent assignment from the astronomers [...] to make some specific calculations" and "to demonstrate the possibility of the existence of quasi-stationary spiral modes from the theoretical point of view [...] with understanding of the dynamical mechanisms relegated to a secondary and even tertiary position" (Lin). ^67,68

"The conclusion in the working hypothesis is not proved or deuce, but supported by an accumulation of theoretical analysis and empirical data. The adoption of this working hypothesis is a very important step in the development of a theory of spiral structure. It means that the authors are committed to back it up with the comparison of subsequent predictions with observational data." (Lin)

The coauthor to share Lin's fame and commitment was his student Frank Shu (Shu 1964) ⁶⁹ who "found it remarkable that a scientist trained as a professional mathematician would place higher priority on empirical facts than deductive reasoning" and believed that "it was this broad-mindedness and clear vision that gave Lin a considerable advantage over his many competitors of the period" (Shu). ⁷⁰ The Lin and Shu paper "On the spiral structure of disk galaxies" (Lin & Shu 1964, hereinafter LS64), in which "they first demonstrated the plausibility of a purely gravitational theory for density waves by a continuum treatment" (Lin & Shu 1966, p.459), appeared in August 1964. ⁷¹

The paper considered small non-axisymmetric disturbances to a razor-thin cold disk and found for them, through the governing hydrodynamic and Poisson equations, wave-like solutions of the type

(12)

each specified by its eigenfunction (r) and a pair of eigenvalues and m. For further advancement, the WKBJ-method was applied. It is valid for the case of phase S(r) varying with radius much faster than amplitude A(r), which features the tightly wrapped spirals, ones of small pitch angle between the circumferential tangent and the tangent to the constant-phase line

(13)

Depending on the sign of a radial-wavenumber function k(r) = - S / r, the spirals are trailing (k > 0) or leading (k < 0) (Fig.8). With A(r) expanded in a series over a small parameter tani = m / kr (i being the pitch angle), the problem is solved to the lowest, i-independent order neglecting the azimuthal force component of spiral gravity. In this case, both leading and trailing arms act as just rings, so that the ensuing dispersion relation

(14)

substantially repeats Toomre's equation (5) for radial oscillations. Importantly, relation (14) is valid for Re{²} 1. This restricts the radial span of the WKBJ solutions, and in the neutral case Im{}= 0 they gain the territory between the Lindblad resonances determined by Eqn (11) and equating the angular speed of an m -armed spiral pattern to a combination

(15)

with the minus/plus sign discriminating, respectively, between the ILR and OLR. The two-armed spirals thus seem preferred as best covering an entire disk (Fig.9).

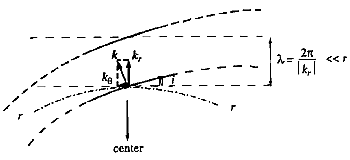Figure 8. The WKBJ approximation and the tightly wrapped spiral waves. kr k and k << k are the components of the local wavenumber k. = 2 / k determines the radial interarm spacing; it is small compared to the galactocentric distance r since kr >> 1 (which is equivalent to small pitch angles i << 1).

Such was the mathematical basis of the original Lin-Shu density-wave theory, called elementary by its authors any later (e.g. Bertin & Lin 1996, p.229). It treated wave quantities _p, , and m as free parameters burdened with no dynamical imposition, which made the theory so comfortable in imitating spiral grand designs by means of the curves r() given by

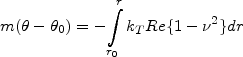(16)

and obtained through the integration of expressions (13) and (14). Sure, the results of this procedure were controvertible, already because the fast-growing waves - exactly those examined in LS64 - ruled out the proclaimed quasi-stationarity. ⁷² But the authors hoped that random motions, excluded from their analysis, would in fact stave off disk instability as definitively as to impose a state of near-stability open for slowly growing modes until a small but finite amplitude.

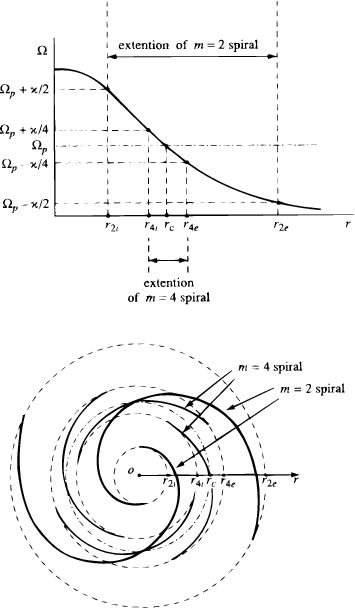Figure 9. The Lindblad resonances as confining the region accessible for the tightly wrapped spiral waves. (a) - a rotation curve for a galaxy disk and its corresponding corotation and m = 2, 4 Lindblad resonances; (b) - the co-scaled view of the two and four armed tightly wrapped spirals.

Toomre (1964) had reflected already on such a state of Q 1 as settling once all over the disk-like stellar Galaxy, but yet he found it stable still, at least in our solar region. As a counterpoise, Lin with Shu diagnosed instability for another region, at about r₀ = 4 - 5 kpc from the center. With that, they pictured "a galactic disk, which is in part stable and in part unstable" and suggested "the possibility of a balance resulting in a neutral density wave extending over the whole disk and having a scale of the order of (but smaller than) the distance between the stable and unstable regions" (LS64, p. 651). It was this "suggestion of the possibility" that summarized Lin's early reflections and made his basic working hypothesis originally sound as a statement that

"the total stellar population, which has various degrees of velocity dispersion, forms a quasi-stationary spiral structure in space of the general nature discussed above" (LS64, p.651).

As we can see, this statement hinges almost entirely on the opinion that, for our galactic disk to be equally stable at that r₀, the velocity dispersion must there exceed c_{r, min} 80 ± 10 km/s, which cannot be the case, else "a considerable number of stars with high radial velocities would reach our neighborhood from the interior part of the Galaxy, contrary to observational evidence" (LS64, p.651). But was this opinion (the authors never repeated it) strong enough? First, it meant an inconceivable situation when some massive portion of a stellar galaxy remains unstable during all the period of formation in it of a global quasi-steady pattern. Secondly, and most important for astronomers, it had - already in 1964 - grave objections to the fact that the largest epicyclic deflection of the Lin-Shu "high radial velocity stars" from their `home' radius r₀ = 4 - 5 kpc, equaled to r r₀ c_r / V₀ 2^1/2, was in frames of Schmidt's model (cited in LS64) 1 - 1.5 kpc only - too little to let those stars even come close from r₀, if not reach us. We find that the original QSSS hypothesis of Lin and Shu, called nowadays "a preliminary formulation" only (Bertin & Lin 1996, p.80), rested on a rather weak basis, both dynamical and empirical.

Very interesting in LS64 is the authors' notice on what had made their work get to print so urgently. A passage following their opening discussion of "at least two possible types of spiral theories", one of which "is to associate every spiral arm with a given body of matter" and the other "is to regard the spiral structure as a [quasi-steady] wave pattern", reads:

"Toomre tends to favor the first of the possibilities described above. In his point of view, the material clumping is periodically destroyed by differential rotation and regenerated by gravitational instability. ⁷³ [...] The present authors favor the second point of view [...] Since A. Toomre's (1964) point of view has been published, it seems desirable to publish our point of view even though the work is not yet as complete as the present writers would wish to have it." (LS64, p.646)

This puzzles. Although it is true that from about 1962 onward Toomre suspected - much as Lynden-Bell had already done in his thesis two years earlier, as it turned out - that at least the more ragged-looking spiral structures result primarily from recurrent gravitational instabilities in the plainly dissipative gas layer of a galaxy (Toomre), there was no explicit discussion of any such suspicions in T64 as actually published. One cannot help but think that this accentuated mention of `Toomre (1964)' was more than just a mistaken reference, that actually it betrayed the influence that at least the cited paper had on Lin.

Shu: "Here, I can only speculate, because certainly my foresight then was not as sharply developed as Lin's. Nor was I privy to the developing estrangement between him and Alar Toomre. [...] Lin had been thinking about the problem of spiral structure nonstop since the Princeton conference in 1961. But he had a world-renowned reputation to protect and therefore was loathe to publish anything hasty before he had worked out his ideas mathematically to his satisfaction. [...] Lin (and later, I) felt strongly that spiral structure was, in essence, a normal mode. But by all the standards of what was then known, a normal mode could not be spiral (unless it grew ridiculously fast). Nevertheless, Lin felt sure that one should not do the naive thing of superimposing equal trailing and leading parts when the wave frequency is (nearly) real. And he probably wanted to discover the reason why before publishing anything. Alar's 1964 paper triggered him into premature action". (Shu)

Lin: "The urgency in my submittal of our paper was to present a different perspective, not to fight for priority". "After reviewing the paper again, I think I could not have done much better or even any better". (Lin)

One way or another, we see that by 1964 Lin indeed had had several thoughts and feelings about spiral modes, and he was eager about gaining power to his perspective. At that, he knew of a growing optimism with shearing or evolving density waves ⁷⁴ and, as well, of the parallel wave-mode interest at Harvard. The T64 paper ⁷⁵ , apart from its engagements on disk stability, did mention Kalnajs' advancing efforts and, still more glaringly, it also mentioned and already discussed Lin's yet unpublished solutions. ⁷⁶ This must have put Lin in a position to urgently patent his views, albeit makeshift in argument for want of better mathematics, and in so doing he rather awkwardly exhibited the opponents' preoccupations as an alternative already placed on record.

3.2. A definitive (?) new prediction

A desirable feature of the WKBJ waves is their mathematical simplicity; their physical relevance to the "grand design" of a spiral galaxy is less transparent.

Kalnajs 1971, p.275

"Just how much did Kalnajs' study of axisymmetric oscillations influence our work? The simple answer is: very little, if at all" (Lin). Such is Lin's judgment regarding the results he had set out in the summer of 1965. ⁷⁷ Those got out of the printer in no less than one year (Lin 1966, 1967a), but an abridged and slightly updated version appeared as soon as February 1966, having become an "Outline of a theory of density waves" by Lin and Shu (1966), labeled `Paper II'.

The three issues reported a WKBJ-styled dispersion relation for the razor-thin hot disk,

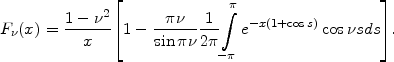	(17)

From its Kalnajs' axisymmetric analog (9)-(10) it differed in the Doppler shift included in and in the form of the reduction factor F(x). ⁷⁸ It was an idea of some such dispersion relation, Lin and Shu (1966) remarked, that had fed originally (LS64) their insight in the disk-stabilizing role of random motions. ⁷⁹

But an important dynamical, not chronological, point was that the hot rotating disk was seen to conduct radial and spiral waves rather distinctly. Given a state of marginal stability, the oscillatory radial neutral mode = / = 0 is well maintained by it along its medium radii (dying out at large r's), ⁸⁰ the local wavelength function ₀(r) depending on mass and angular momentum distributions. In contrast, the spiral wave cannot be neutral as extendibly: its Doppler-shifted frequency - m(r) gets r -dependent. This ties the neutrality condition = ( - m) / = 0 to a narrow corotation zone of r r_c, and there only can the interarm spacing (r) equal ₀(r), the rest of disk getting more and more stable against the wave as one travels away from r_c in or out. If so, why not to try to juxtapose the basic Lin-Shu concept of a balance and the solar-region stability inference by Toomre? For this, it seems sufficient to send corotation way beyond - to an outer disk region supposedly as permissive to marginal stability as to admit it - and to cancel all instability inside that r_c in favor of Q 1. Lin and Shu did seem to have followed this way. Moreover, they adopted a Q 1 model (discussed already in T64), being captured by a picture of overstability, i.e. gradient instability held to mildly develop over the system and to provide some selective amplification of trailing, not leading, waves.

Besides, relation (17) tells (k) to decrease with wavenumber till k remains under some k₀, and then to rise up at k back to unity. Any intermediate value of is met thus twice, meaning two branches of WKBJ solutions, the shorter- and the longer-wave ones, their forms r() being provided by equation (16) with F(x) added in the integrand denominator. If Q 1, the branches join at corotation, showing there equal interarm spacings _sw(r_c) = _lw(r_c) = ₀(r_c). This value is the largest (smallest) for the shortwave (longwave) branch: _sw(r) falls down until zero (_lw(r) ) as one goes from corotation to ILR. Aimed from the outset at explaining the observed 2-3 kpc local spacings, Lin got tempted to acknowledge the shortwave branch, the more so as, not to forget, in 1964 he had had no choice when having to comment on this same gas-given spacing on the basis of relation (14) that seized but one - long-wave (!) - branch. ⁸¹ But things did not get all as clear by 1966, and this is why neither Lin (1966, 1967a) nor Lin and Shu (1966) were eager to go into the wave-branch question, keeping silent about any graphic view of their newer formula. Only at the Noordwijk IAU Symposium (August, 1966) they gave a graph, it displayed the short-wave-branch extension of the () curve (Fig.10) on which they built a model for the full spiral of our Galaxy (Fig.11), tentatively two-armed and answered by a remote corotation (Lin & Shu (1967). ⁸² Spirals of this class show as slow a rotation as to almost guarantee the ILRs be present and lie in a relative proximity from the center. Namely, Lin and Shu connected our `home' m= 2 ILR with the `3-kpc arm' which fixed the spiral pattern speed _p = 11 km/s/kpc.

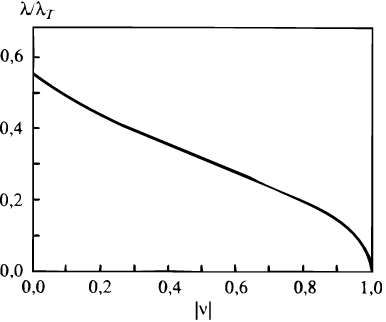Figure 10. The short-wave branch of the dispersion relation (17) for a Q = 1 disk model. (The figure is reproduced from Lin & Shu 1967)

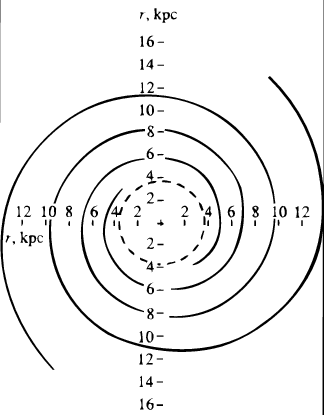Figure 11. The Lin-Shu model for the Galactic spiral density wave. The model is calculated with the help of the dispersion curve in Fig.10. The dashed line shows the ILR region taken to be the residence of the `3-kpc arm'. This provides the patter