<< 1.12. Цели ясны, нужны указания | Оглавление | 1.14. Попытка объять необъятное >>

1.13. По большому и малому кругам

Искусственные спутники Земли совершают сложные движения относительно наблюдателя. Тем не менее, в каждый момент наблюдений можно подобрать большой круг, хорошо представляющий перемещения объекта по небесной сфере на коротком интервале времени.

Обозначим через , прямое восхождение и склонение полюса большого круга, а посредством , - положение точки верхней кульминации. Справедливы простые соотношения

На два соседних момента времени , вычислим топоцентрические экваториальные координаты объекта

Векторное произведение содержит координаты полюса большого круга, проведенного через векторы и ,

На любой момент времени из интервала вычислим топоцентрический вектор объекта в экваториальной системе . Угол , отсчитываемый по большому кругу от точки верхней кульминации, определяется формулами

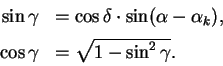
Скорость изменения угла , величину , нетрудно найти методом численного дифференцирования:

Четырехосная установка позволяет использовать малый круг небесной сферы для наблюдений прохождения спутника. Пусть , - величины, близкие к значениям азимута и высоты точки верхней кульминации объекта. Полюс , для ориентации прибора назначим формулой

поворот вокруг четвертой оси на угол в плоскости, проходящей через точки полюса и верхней кульминации, приведет к тому, что вектор, совпадающий с направлением наблюдения, будет очерчивать на небесной сфере с изменением угла положения малый круг.

Параметры малого круга: установочные азимут и высота , угол и угол положения вычисляются в горизонтальной системе координат с помощью метода наименьших квадратов. Необходимо провести плоскость, заданную уравнением

и аппроксимирующую положения спутника с высотой и азимутом на сфере единичного радиуса

в различные моменты времени за весь интервал прохождения выше заданного значения высоты .

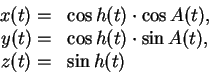
Для моментов времени вычисляем суммы произведения разностей

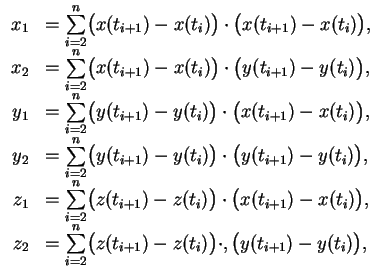
определяем коэффициенты , ,

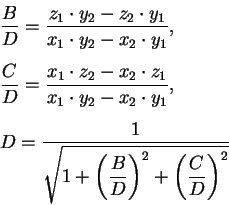
и установочные параметры

---

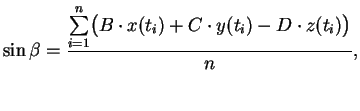
<< 1.12. Цели ясны, нужны указания | Оглавление | 1.14. Попытка объять необъятное >>

Публикации с ключевыми словами: астрометрия - лазерная локация Публикации со словами: астрометрия - лазерная локация
См. также: Достижения космической астрометрии Скончался Константин Владиславович Куимов Красная Луна и зелёный луч Константину Владиславовичу Куимову – 75 лет Саймон Ньюком (1835 -1909) к 175-летию со дня рождения. Вращение Земли и продолжительность суток 80 лет со дня рождения Альберта Петровича Гуляева Все публикации на ту же тему >>