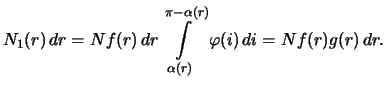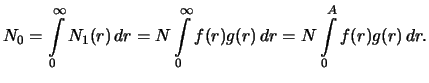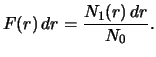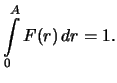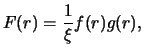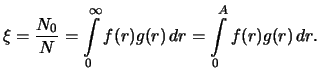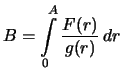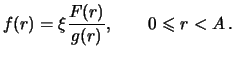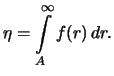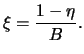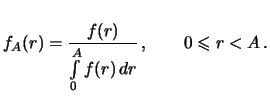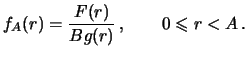О распределении больших полуосей орбит внесолнечных планет
<< 3. Вероятность обнаружения планеты
| Оглавление |
5. Численные результаты >>
Эффект селекции отражен формулой (
4): планет, имеющих
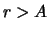
, мы не видим совсем; при
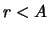
шансы планеты быть
обнаруженной стремительно растут с уменьшением

. С ростом
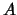
(т. е. с увеличением
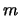
и уменьшением ошибки наблюдений
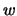
)
эффект селекции уменьшается.
Полностью эффект селекции выявляется в трансформации функций
распределения.
Пусть имеется большое число
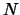
наблюденных звезд, имеющих каждая по
планете с круговой орбитой. Пока в нашем распоряжении слишком мало
данных,
чтобы оперировать с многомерными распределениями
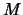
,
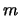
,

,
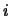
.
Ограничимся простейшей одномерной задачей. Именно, фиксируем
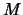
,
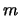
;
предположим независимость распределений

,
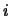
; изотропность
ориентации
вектора площадей. Тогда статистическая ситуация полностью описывается
плотностью вероятности
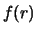
: число планет с расстоянием от

до
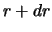
равно
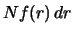
.
Найдем плотность вероятности
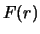
величины
 среди открытых
планет
среди открытых
планет.
Очевидно, число планет с расстояниями от

до
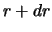
и наклонами от
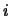
до
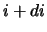
равно
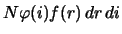
. Число
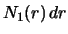
открытых
планет с расстояниями между

и
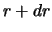
равно
Число всех открытых планет
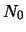
есть
Доля открытых планет с расстояниями от

до
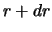
среди всех открытых
планет есть
Окончательно,
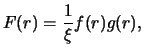 |
(5) |
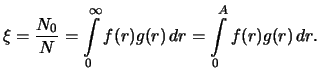 |
(6) |
Величина
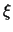
совпадает с вероятностью открытия планеты с данными
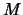
,
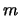
и случайными
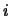
,

. Обратим внимание, что
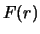
равна нулю при
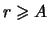
.
Формулы (
4)-(
6) конструктивно определяют
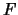
, если
известна
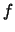
. Однако относительно
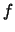
мы можем пока лишь строить
догадки. В то же время
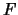
может быть найдена (пусть пока не очень
уверенно) из наблюдений.
Решим обратную задачу построения
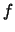
по известной
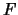
.
Дана непрерывная неотрицательная функция
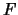
, определенная на
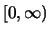
,
равная нулю на
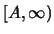
и такая, что интеграл
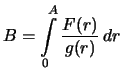 |
(7) |
сходится. Так как
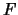
- плотность вероятности, то потребуем еще
Из (
5) следует
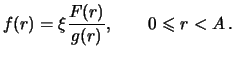 |
(8) |
Легко проверить, что (
6) выполняется при любом
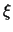
, если
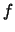
определяется равенством (
8). Чтобы найти
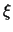
, вычислим
интеграл от обеих частей (
8) по промежутку
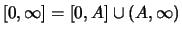
:
где
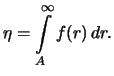 |
(9) |
Фиксируем произвольное
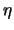
,
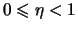
. Тогда
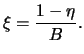 |
(10) |
Так как
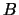
известно, то формула (
10) определяет положительное
число
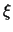
, после чего (
8) дает нам
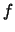
при
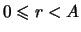
.
Итак, мы нашли
все функции
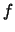
, дающие наблюдаемую плотность
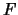
. Правее точки
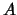
распределение
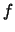
неизвестно. Левее функция
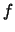
определена с точностью до множителя
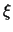
. Это важная
информация, т. к. она содержит исчерпывающие сведения о
распределении расстояний

среди всех планет, расположенных не
далее
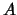
от своей звезды.
Действительно, обозначим через
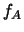
соответствующую плотность
вероятности. По определению
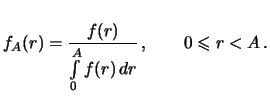 |
(11) |
Подставляя в числитель и знаменатель следующее из (
5) выражение
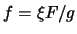
, получим искомое
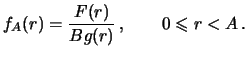 |
(12) |
Из (
11), (
9) вытекают полезные соотношения
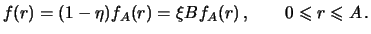 |
(13) |
Следует помнить, что
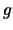
безразмерна,
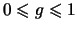
;
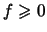
,
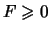
,
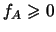
имеют размерность
[м
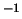
];
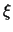
,
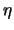
и
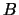
безразмерны, связаны соотношением
(
10), причем
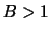
,
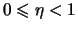
,
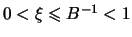
.
<< 3. Вероятность обнаружения планеты
| Оглавление |
5. Численные результаты >>