Луна - спутник или планета?
К.В.ХОЛШЕВНИКОВ
Санкт-Петербургский государственный университет
|
Иногда профессионалы относят Луну к самостоятельным планетам Солнечной системы, поскольку существует несколько критериев различения планет и спутников. Основная цель статьи - рассказать об этих критериях, о важных для астрономии и космонавтики гравитационных сферах. |
Введение
|
Похожий разговор вполне мог состояться еще в III веке до н.э. Ведь уже Аристарх Самосский обосновал движение Луны вокруг Земли, а менее ярких блуждающих светил и Земли вокруг Солнца. И тем не менее вынесенный в заголовок вопрос отнюдь не так прост, как казалось Аристарху и Копернику. Подобно электрону, проявляющему свойства как частицы, так и волны, Луна в своем движении проявляет свойства как спутника, так и планеты. Обоснованию этого непривычного для многих утверждения и посвящена настоящая статья.
Математическая модель
На движение Луны влияет масса явлений: притяжение кольца Сатурна, Магеллановых облаков, удары метеоритов и космических аппаратов. Но для ответа на вынесенный в заголовок вопрос достаточно учесть лишь главные причины, определяющие качественное поведение лунной орбиты. Оказывается, можно ограничиться следующей простой моделью: на Луну действует только ньютоновское притяжение Земли и Солнца, причем все три тела можно считать материальными точками. Докажем это утверждение.
По закону всемирного тяготения любое светило притягивает Луну слабее, чем Солнце, в k раз,
|
|
(1) |
Здесь m1 , m2 - массы Солнца и светила; r1 , r2 - расстояния от Луны до этих тел. Ясно, что хоть какую-то конкуренцию Земле и Солнцу могут составить лишь большие планеты Солнечной системы, а звезды, туманности, метеориты, релятивистские эффекты и прочее можно оставить поэтам.
Среди планет земной группы наибольшей массой m2 и одновременно наименьшим из возможных расстояний r2 обладает Венера, для остальных планет эту роль исполняет Юпитер. Значение k для Венеры минимально при одновременном выполнении следующих условий: Венера в афелии; Земля в перигелии; Луна в апогее; наблюдаются кольцеобразное солнечное затмение и нижнее соединение Венеры. Аналогично в случае Юпитера должно быть: Юпитер в перигелии; Земля в афелии; Луна в апогее; наблюдаются полное лунное затмение и противостояние Юпитера. Подставляя в (1) соответствующие значения масс и расстояний [1], получим
k (Венера) ![]() 27
27 ![]() 103, k (Юпитер)
103, k (Юпитер) ![]() 16
16 ![]() 103.
103.
Полученные оценки относительных величин сил (или, что то же, ускорений) описывают их влияние на траекторию Луны в инерциальной или близкой к ней гелиоцентрической системе отсчета. Но чаще всего нас интересует геоцентрическое движение, и тут самое время вспомнить о лифте Эйнштейна. Сила, приводящая к ускорению даже в парсек за квадратную секунду, никак не отразится на движении Луны относительно Земли, если это ускорение одинаково для обоих тел, иными словами, если силовое поле однородно. Эффекты в геоцентрическом движении вызываются разностью ускорений поля в точках, где находятся центры масс Луны и Земли. Подобные разности принято называть приливными ускорениями, свойства и роль которых в жизни Вселенной прекрасно описаны в [2]. В частности,
|
|
(2) |
Здесь ![]() - наибольшее значение модуля вызываемого Солнцем приливного ускорения в геоцентрическом движении Луны при всех мыслимых положениях последней на расстоянии r1 от Солнца и
- наибольшее значение модуля вызываемого Солнцем приливного ускорения в геоцентрическом движении Луны при всех мыслимых положениях последней на расстоянии r1 от Солнца и ![]() от Земли. Формула (2), разумеется, описывает приливное влияние любого тела, надо только изменить значения m1 , r1 .
от Земли. Формула (2), разумеется, описывает приливное влияние любого тела, надо только изменить значения m1 , r1 .
Обозначая через k0 = (r2 / r1)k отношение ![]() для Солнца и какой-либо планеты, получим
для Солнца и какой-либо планеты, получим
k0(Венера) ![]() 7
7 ![]() 103, k0(Юпитер)
103, k0(Юпитер) ![]() 60
60 ![]() 103.
103.
До сих пор мы считали небесные тела точками или, что то же, телами сферической структуры - шарами с плотностью, зависящей лишь от расстояния до центра. Гравитационное ускорение, индуцируемое произвольным телом конечных размеров, может существенно отличаться от такового для шара. Но, как заметили еще древние софисты, издали любая башня кажется круглой. В нашем случае, согласно [3], прямое солнечное притяжение превышает эффект сжатия Земли по крайней мере в 1,9 ![]() 106 раз, а приливное - в 9
106 раз, а приливное - в 9 ![]() 103 раз.
Итак, в качественном описании движения Луны достаточно приближения задачи трех тел (точек).
103 раз.
Итак, в качественном описании движения Луны достаточно приближения задачи трех тел (точек).
Гравитационные сферы
В небесной механике и космонавтике часто пользуются удобным понятием гравитационной сферы. Пусть малое тело P (Луна) движется в ньютоновском поле тел Q1 (Солнце) и Q (Земля) массами m1 и m соответственно. Пространство возможных положений P можно разбить на две части: область T, где доминирует притяжение Q, и остальное пространство T1 . Область T называют гравитационной сферой Q по отношению к Q1 . Часто так же называют и границу S между T и T1 , что не приводит к путанице.
Приведенное определение становится полным, как только мы придадим точный смысл понятию "доминировать". Полезны различные трактовки последнего, так что в астрономии несколько гравитационных сфер.
Расположение тел опишем векторами R = Q1Q, r = Q1P, ![]() = QP (рис. 1). Их модули будем обозначать теми же, но не жирными буквами.
= QP (рис. 1). Их модули будем обозначать теми же, но не жирными буквами.
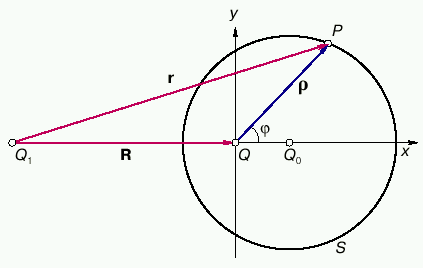 |
| Рис. 1.Сфера тяготения |
Сфера тяготения
Так называется простейшая из гравитационных сфер S, выделяемая условием: силы притяжения точки P со стороны Q1 и Q равны между собой:
|
|
(3) |
Проведем ось x декартовой системы координат через точки Q1 , Q. Начало отсчета совместим с Q. Положения осей y, z безразличны. Запишем координаты трех интересующих нас векторов:
R = (R, 0, 0) ![]() = (x, y, z) r = R +
= (x, y, z) r = R + ![]() = (R + x, y, z).
= (R + x, y, z).
Уравнение (3) элементарно преобразуется к виду
| (x - A)2 + y2 + z2 = B2, | (4) |
где
A=![]() , B=
, B=![]() ,
, ![]()
Поскольку ![]() , то
, то ![]() , 0 < A < B.
, 0 < A < B.
Согласно (4) , сфера тяготения оказалась геометрической сферой. Ее радиус равен B, а центр расположен в точке Q0 на оси x на расстоянии A справа от Q, причем Q лежит внутри S. Область T - шар, внутренность S. Рисунок 1 изображает сечение S плоскостью xy. Сфера S движется вместе с телами Q1 , Q и меняет свои размеры вместе с R (параметр ![]() постоянен).
постоянен).
Для пары Солнце-Земля величина R колеблется от 0,983 а.е. (а.е. - астрономическая единица), зимой до 1,017 а.е. летом. Соответственно A и B изменяются в пределах 442 ![]() A
A ![]() 457 км, 255
457 км, 255 ![]() 103
103 ![]() B
B ![]() 264
264 ![]() 103 км. Смещение A центра Q0 от Q оказалось в 14 раз меньше радиуса Земли, и им можно пренебречь. Но это малоинтересно. Замечательно, что B почти вдвое меньше расстояния Земля-Луна! Луна находится вне сферы тяготения Земли, причем достаточно далеко. В связи с этим можно упомянуть, что Солнце притягивает Луну в два раза сильнее Земли.
103 км. Смещение A центра Q0 от Q оказалось в 14 раз меньше радиуса Земли, и им можно пренебречь. Но это малоинтересно. Замечательно, что B почти вдвое меньше расстояния Земля-Луна! Луна находится вне сферы тяготения Земли, причем достаточно далеко. В связи с этим можно упомянуть, что Солнце притягивает Луну в два раза сильнее Земли.
Итак, с точки зрения сферы тяготения Луна - планета, а не спутник. Если внезапно остановить Землю, то Луна бросит ее и будет продолжать одна свой обычный путь вокруг Солнца.
Сфера действия
Определение введенной П. Лапласом сферы действия много сложнее. Для простоты пренебрежем массой Луны. Представим ускорение w Луны в невращающейся системе отсчета с центром в Земле в виде
| w = W + Z, | (5) |
где W - невозмущенное ускорение от притяжения Земли, а Z - возмущающее от действия Солнца. По правилу лифта Эйнштейна Z есть разность ускорений, вызываемых Солнцем в точках P и Q. Мы уже знаем, что последние величины примерно в два раза больше W, но их разность мала. При фиксированном ![]() значение Z с очевидностью максимально во время солнечного затмения, когда r = R -
значение Z с очевидностью максимально во время солнечного затмения, когда r = R - ![]() . Прямой подсчет дает
. Прямой подсчет дает
|
|
(6) |
Если в (5) пренебречь слагаемым Z, получим простое дифференциальное уравнение, описывающее задачу двух тел, решенную еще Ньютоном. Добавочное ускорение Z вносит возмущение в эллиптическое движение Луны тем меньшее, чем меньше отношение Z / W.
Повторим те же рассуждения в гелиоцентрической системе отсчета, заменив (5) на
| w1 = W1 + Z1 . | (7) |
Ускорение w1 Луны разбито на невозмущенное W1 от притяжения Солнца и возмущающее Z1 , вызванное действием Земли. Легко показать, что
|
|
(8) |
Сопоставим оценки (6) и (8): возмущения гелиоцентрического эллипса лунной орбиты в 54 раза превосходят возмущения геоцентрического эллипса. Наглядность этому результату придает понятие сферы действия. Последняя определяется как поверхность S, на которой
|
|
(9) |
Внутри сферы действия, то есть в области T, задаваемой соотношением (9) с заменой знака равенства на знак "меньше", выгоднее пользоваться уравнениями (5), вне - уравнениями (7). Оценки (6), (8) показывают, что Луна находится глубоко внутри сферы действия Земли.
Таким образом, с точки зрения сферы действия Луна - спутник, а не планета.
Исследуем форму сферы действия. Запишем ее уравнение (9) в той же системе координат, в которой получено (4). После преобразований
|
|
(10) |
где
![]()
![]()
Поскольку уравнение (10) содержит y, z только в комбинации y2 + x2, то S есть поверхность вращения вокруг оси x. Поэтому форма S определяется формой кривой S' - сечением S плоскостью xy.
Преобразуя (10) средствами компьютерной алгебры, студент астрономического отделения Ленинградского университета С.Р. Тюрин[4] нашел, что S' совпадает или является частью алгебраической кривой 48-й степени от x, y. Можно показать, что S' представляет собой близкий к кругу, симметричный относительно обеих осей овал, сжатый по оси x (оси затмений). Расстояние ![]() изменяется от 792
изменяется от 792 ![]() 103 до 940
103 до 940 ![]() 103 км, что в два раза превышает наибольший радиус лунной орбиты.
103 км, что в два раза превышает наибольший радиус лунной орбиты.
Сфера хилла
Для простоты будем пренебрегать массой Луны и эксцентриситетом земной орбиты. Как показал В.Г. Голубев [5], без этих предположений можно обойтись, но мы не будем усложнять задачу.
Уточним направление оси y. Проведем ее в плоскости круговой орбиты Q в сторону движения. Начало Q системы xyz описывает окружность радиуса [m1 / (m1 + m)]R вокруг центра масс Q1 и Q, а сама система равномерно вращается вокруг оси z с угловой скоростью ![]() , определяемой по третьему закону Кеплера. Движение P в системе xyz вызывается силами притяжения к Q1 и Q, а также центробежной и кориолисовой силой инерции. Как известно, кориолисова сила не производит работы, а остальные три силы консервативны. Поэтому сохраняется сумма кинетической и потенциальной энергии P, складывающейся из энергии сил притяжения и центробежной. После сокращения на массу P можно записать
, определяемой по третьему закону Кеплера. Движение P в системе xyz вызывается силами притяжения к Q1 и Q, а также центробежной и кориолисовой силой инерции. Как известно, кориолисова сила не производит работы, а остальные три силы консервативны. Поэтому сохраняется сумма кинетической и потенциальной энергии P, складывающейся из энергии сил притяжения и центробежной. После сокращения на массу P можно записать
![$\frac{\upsilon^{2}}{2} = \frac{Gm_{1}}{r} + \frac{Gm}{\rho}+ \frac{\omega^{2}}{2}\left[ \left(\frac{m_{1}}{m_{1}+m} R + x \right)^{2} +y^{2}\right] $](https://images.astronet.ru/pubd/2001/10/14/0001171221/tex/formula21.gif) -
-
|
|
(11) |
Здесь ![]() - скорость P, h - безразмерная постоянная, называемая постоянной Якоби в честь получившего интеграл движения (11) немецкого ученого. Поскольку
- скорость P, h - безразмерная постоянная, называемая постоянной Якоби в честь получившего интеграл движения (11) немецкого ученого. Поскольку ![]() 0, то справа в (11) стоит величина, неотрицательная во все время движения.
0, то справа в (11) стоит величина, неотрицательная во все время движения.
Часть пространства, выделяемую соответствующим неравенством, называют областью возможных движений. Ее граница S задается уравнением
![$\frac{2m_{1}R}{r} + \frac{2mR}{\rho} + \frac{m_{1} + m}{R^{2}}\left[\left(\frac{m_{1}}{m_{1}+m}R +x \right)^{2} + y^{2} \right]=$](https://images.astronet.ru/pubd/2001/10/14/0001171221/tex/formula25.gif)
|
= |
(12) |
и называется поверхностью нулевой скорости или поверхностью Хилла в честь американского астронома и математика, который ввел это понятие.
Очевидно, при больших h поверхность Хилла имеет окружающую Q компоненту S0 , близкую к сфере ![]() . С уменьшением h увеличивается S0 .
. С уменьшением h увеличивается S0 .
Сферой Хилла называют наибольшую из выпуклых поверхностей S0 , окружающих Q. В нашем случае сфера Хилла представляет собой квазисферу, радиус которой меняется от 940 ![]() 103 до 1500
103 до 1500 ![]() 103 км.
103 км.
Таким образом, Луна движется глубоко внутри сферы Хилла и с этой точки зрения является спутником Земли.
Кривизна траектории
Геоцентрическая орбита Луны - пространственная кривая. Но ее "пространственность" невелика. Векторы скорости и ускорения образуют с плоскостью эклиптики углы не более 6°. То же верно и для гелиоцентрической траектории. Поэтому в обоих случаях достаточно ограничиться проекцией орбиты на плоскость эклиптики. Как хорошо известно, орбита Луны относительно Земли близка к кеплеровскому эллипсу. Кстати, мы проиллюстрировали это, оценив Z / W в предыдущем разделе. Проекция лежащего в плоскости ![]() эллипса на ортогональную
эллипса на ортогональную ![]() плоскость
плоскость ![]() - отрезок, проекция на любую другую плоскость тоже эллипс. Поэтому проекция L геоцентрической орбиты Луны на плоскость эклиптики близка к эллипсу. Отклонения от него может заметить на глаз лишь художник или чертежник. Только одно отличие заметно просто человеку с нормальным зрением: орбита не замыкается после оборота вокруг Земли. Каждый следующий виток чуть-чуть смещен по отношению к предыдущему. Но это несущественно. Для нашей цели важны два обстоятельства:
- отрезок, проекция на любую другую плоскость тоже эллипс. Поэтому проекция L геоцентрической орбиты Луны на плоскость эклиптики близка к эллипсу. Отклонения от него может заметить на глаз лишь художник или чертежник. Только одно отличие заметно просто человеку с нормальным зрением: орбита не замыкается после оборота вокруг Земли. Каждый следующий виток чуть-чуть смещен по отношению к предыдущему. Но это несущественно. Для нашей цели важны два обстоятельства:
- вектор скорости на L вращается влево, если смотреть с северного полюса эклиптики; кривизна всегда положительна, точки перегиба не встречаются;
- на одном витке L вокруг Земли отсутствуют петли.
Оба свойства вместе означают, что L всегда обращена вогнутостью к Земле, не имея ни волн (кривизна всегда положительна), ни петель на одном витке (кривизна не слишком велика), и похожа на овал с заключенной внутри Землей (рис. 2). Интересно, что оба указанных свойства (с заменой слова "Земля" на слово "Солнце") справедливы и для проекции гелиоцентрической орбиты Луны. Таким образом, с точки зрения кривизны траектории Луна с равным правом может считаться и спутником и планетой.
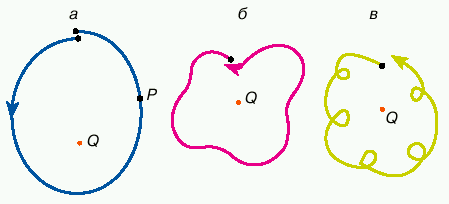 |
| Рис. 2. Геоцентрические траектории Луны (а); орбита знакопеременной кривизны (б ); петляющая орбита (в) |
Заключение
Мы построили математическую модель движения Луны, адекватную задаче. Это построение демонстрирует общее правило, упомянутое, например, в [6]. Во-первых, мы из общих соображений отобрали факты, которые в принципе могут играть хоть какую-то роль в изучаемом явлении, и отбросили практически бесконечную совокупность остальных. Во-вторых, мы оценили сравнительное действие отобранных и также отбросили их все, за исключением двух основных. Последние необходимо учитывать обязательно, иначе модель потеряет связь с действительностью.
Мы рассмотрели нашу модель с разных сторон, введя несколько понятий, полезных и во многих других отношениях. И выяснили следующее. В большинстве случаев Луну следует считать спутником Земли, как это и делают подавляющее большинство ее грамотных жителей. Но бывают ситуации, когда Луна ведет себя как планета, например она вместе с Венерой находится вне сферы тяготения Земли. Наконец, встречаются ситуации, когда Луна ведет себя одновременно и как спутник и как планета, например формы ее геоцентрической и гелиоцентрической траекторий схожи. Все это служит превосходной иллюстрацией того, что не только в квантовой механике, казалось бы, взаимоисключающие утверждения оба оказываются верными.
Заметим, что наши рассуждения применимы и к другим спутникам планет. Например, практически все искусственные спутники Земли находятся глубоко внутри сферы ее тяготения. Так что ИСЗ - настоящие спутники с точки зрения любых гравитационных сфер. И с точки зрения формы траектории тоже: их гелиоцентрические орбиты волнисты. Спутники других планет любознательный читатель может исследовать сам.
Литература
| [1] | Астрономический ежегодник на 1997 г. / Ред. В.К. Абалакин. СПб.: ИТА РАН, 1996. |
| [2] | Сурдин В.Г. Приливные явления во Вселенной // Новое в жизни, науке, технике. Сер. Космонавтика, астрономия. М.: Знание, 1986. No 2. |
| [3] | Антонов В.А., Тимошкова Е.И., Холшевников К.В. Введение в теорию ньютоновского потенциала. М.: Наука, 1988. |
| [4] | Тюрин С.Р. Исследование точного уравнения сферы действия // Тез. докл. на студ. науч. конф. "Физика Галактики", 1989 г. Свердловск, Изд-во УрГУ, 1989. С. 23. |
| [5] | Голубев В.Г., Гребеников Е.А. Проблема трех тел в небесной механике. М.: Изд-во МГУ, 1985. |
| [6] | Неймарк Ю.И. Простые математические модели и их роль в постижении мира// Соросовский Образовательный Журнал. 1997. No 3. С. 139-143. |
|
Публикации с ключевыми словами:
сферы гравитационного влияния - спутники планет - Небесная механика - Луна - планеты
Публикации со словами: сферы гравитационного влияния - спутники планет - Небесная механика - Луна - планеты | |
См. также:
Все публикации на ту же тему >> | |