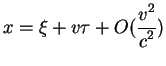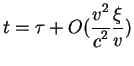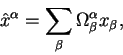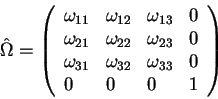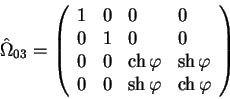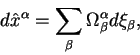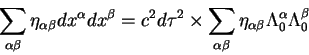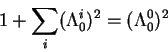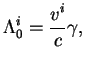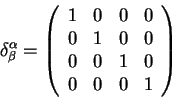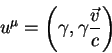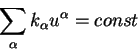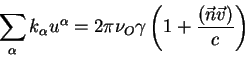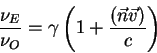Rambler's Top100Astronet    
  по текстам   по ключевым словам   в глоссарии   по сайтам   перевод   по каталогу 		 

На первую страницу
Теория относительности для астрономов
<< 1. Принципы относительности | Оглавление | 3. Ускоренные системы отсчета >>

Разделы

2. Специальная теория относительности

Астрономы наблюдают электромагнитное излучение (свет) небесных источников в различных диапазонах спектра. Хотя само излучение характеризуется целым набором параметров, для астрономии важны следущие: направление прихода света, его частота, а также иногда интенсивность. Для большинства астрономических задач волновая природа электромагнитного излучения также не играет решающей роли. Обычно большинство задач с успехом может быть решено в приближении геометрической оптики принимаемых фотонов, включая даже фотоны радиодиапазона. Лишь несколько задач требуют учета волновой природы, например, задачи интерферометрии. Однако, для вычисления многих задач интерферометрии достаточно знания только параметров излучения, найденных в пределе геометрической оптики. Поэтому мы будем работать с основным параметром характеризующими излучение в пределе геометрической оптики - волновым вектором излучения. Направление прихода лучей света и его частота в специальной теории относительности объединяются в единый вектор - 4$^x$ импульс фотона.

Поэтому одной из основных наших задач будем вывод уравнений редукции и их решения для четырехмерного вектора импульса фотона.

2.1 Кинематика специальной теории относительности

Прежде чем выводить основные кинематические уравнения СТО сформулируем принцип постоянства скорости света на языке математики.

Рассмотрим опять две системы, движущиеся равномерно и прямолинейно друг относительно друга. Будем считать, что система $K$ неподвижна относительно наблюдателя, а система $\hat K$ движется со скоростью $v$. Пусть в $K$ из точки с координатами $(x_1,$ $y_1,$ $z_1)$ в момент $t_1$ выходит луч света и достигает точки с координатами $(x_2,$ $y_2,$ $z_2)$ в момент $t_2$. В системе $\hat K$ эти два события выглядят следущим образом. В момент $\hat t_1$ из точки с координатами $(\hat x_1,$ $\hat y_1,$ $\hat z_1)$ выходит луч света, который попадает в точку с координатами $(\hat x_2,$ $\hat y_2,$ $\hat z_2)$ в момент времени $\hat t_2$.

Из уравнений теории электромагнитного поля ( уравнений Максвелла) мы знаем, что пространственно - временная точка $(x_1,$ $y_1,$ $z_1$, $t_1)$ связана с пространственно - временной точкой $(x_2,$ $y_2,$ $z_2$, $t_2)$ равенством вида:

\begin{displaymath} (x_1 -x_2)^2 + (y_1 -y_2)^2 +(z_1 -z_2)^2 =c^2 (t_1 -t_2)^2 \end{displaymath} (2.1)

Здесь $c$ -скорость света. Постулат об одинаковости скорости света в обеих системах координат можно сформулировать так, что равенство (2.1) справедливо и в системе координат $\hat K$:

\begin{displaymath} (\hat x_1 -\hat x_2)^2 + (\hat y_1 -\hat y_2)^2 +(\hat z_1 -\hat z_2)^2 =c^2 (\hat t_1 -\hat t_2)^2 \end{displaymath} (2.2)

Обратим внимание, что в системе $\hat K$ уравнение содержит $c$, а не $\hat c$, поскольку две эти величины равны друг другу.

Теперь будем считать, что точки 1 и 2 лежат бесконечно близко друг к другу, а также будем считать, что интервал времени для распространения света из 1 в 2 является бесконечно малым. Тогда упомянутые равенства можно записать как:

\begin{displaymath} dx^2 + dy^2 +dz^2 =c^2 dt^2 \end{displaymath} (2.3)

Введем теперь понятие 4$^x$ мерного интервала между двумя событиями. Будем называть первым событием то, которое произошло в точке с координатами $(x,$ $y,$ $z)$ в момент $t$, а вторым событием то, которое произошло в точке с координатами $(x+dx,$ $y +dy,$ $z +dz)$ в момент $t +dt$. Определим 4$^x$ мерный интервал между первым и вторым событием как расстояние в псевдоэвклидовом пространстве:

\begin{displaymath} ds^2 =c^2 dt^2 -dx^2 - dy^2 -dz^2 \end{displaymath} (2.4)

Из инвариантности скорости света следует, что интервал между двумя событиями - излучением света из какой -либо пространственной точки и приемом света в другой точке равен нулю в любой инерциальной системе отсчета. Т.е. $ds=0$ в системе $K$ и $\hat ds=0$ в системе $\hat K$.

4$^x$ мерный интервал является инвариантом при преобразованиях координат, его величина не зависит от того в какой системах отсчета рассматриваются координаты между событиями. Воспользуемся этим свойством для вывода правильных преобразований координат между двумя системами, которые движутся относительно друг друга.

2.1.1 Преобразования между инерциальными системами

Рассмотрим две движущиеся системы координат. Из принципа постоянства скорости света, а также из инвариантности $4^x$ мерного интервала можно заключить, что в двух системах координат $K \in (t,x)$ и $\Xi \in (\tau, \xi)$, связанных линейными преобразованиями вида 2.1:

$\displaystyle x=\xi \alpha +c\tau \beta$ (2.5)
$\displaystyle ct= c \tau \alpha + \xi \beta$  

должны совпадать дифференциалы интервала между двумя событиями:
$\displaystyle ds^2= c^2dt^2- dx^2 \mbox{\hskip1cm в системе $K$}$ (2.6)
$\displaystyle ds^2= c^2d\tau^2- d\xi^2 \mbox{\hskip1cm в системе $\Xi$}$  

Коэффиценты преобразования $\alpha, \beta$ проще всего выбрать в виде:

$\displaystyle \alpha=\ch \psi$ (2.7)
$\displaystyle \beta =\sh \psi$  

Рассмотрим дифференциалы (2.5) и подставим их в выражения для 4$^x$ мерного интервала. Легко видеть, что равенство

\begin{displaymath} \ch^2 \psi -\sh^2 \psi=1 \end{displaymath}

обеспечивает инвариантность интервала:

\begin{displaymath} c^2dt^2-dx^2=c^2d\tau^2 -d\xi^2. \end{displaymath}

Раасмотрим теперь связь угла $\psi$ в выражениях для гиперболических синуса и косинуса со скоростью системы $\hat K$ относительно системы $K$. Рассмотрим движение центра системы $\hat K$ в системе координат $K$. Центр системы координат $\Xi$ находится в точке $\xi=0$. В системе координат $K$ точка $\xi=0$ движется согласно системе уравнений:

$\displaystyle x=c \tau \sh \psi$ (2.8)
$\displaystyle ct= c \tau \ch \psi$  

Отсюда легко заключить, что центр системы координат $\Xi$ движется в системе $K$ со скоростью:

\begin{displaymath} {\displaystyle x\over\displaystyle ct}={\displaystyle v\over\displaystyle c}=\th \psi \end{displaymath}

Теперь выражая гиперболические синус и косинус через гиперболический тангенс приходим к уравнениям для преобразования координат:

$\displaystyle x={\displaystyle\xi +v\tau\over\displaystyle\sqrt{1-{\displaystyl... ...le c^2}\xi\over\displaystyle\sqrt{1-{\displaystyle v^2\over\displaystyle c^2}}}$ (2.9)

Отметим, что преобразования (2.9) больше похожи на преобразования типа вращения (1.3), а не преобразования Галилея (1.1). Рассмотрим теперь предел малых скоростей, когда ${\displaystyle v\over\displaystyle c} \ll 1$, разложим преобразования (2.9) в ряд Тэйлора по степеням этого малого параметра и оставим только линейные величины по ${\displaystyle v\over\displaystyle c} \ll 1$ пренебрегая квадратичными и более высокими степенями отношения взаимной скорости движения систем к скорости света:

$\displaystyle x=\xi +v\tau +O({\displaystyle v^2\over\displaystyle c^2})$ (2.10)
$\displaystyle \qquad$ (2.11)
$\displaystyle t=\tau + O({\displaystyle v^2\over\displaystyle c^2}{\displaystyle\xi\over\displaystyle v})$ (2.12)

Второй член в пребразовании времени выписан специально для того, чтобы продемонстрировать, что в преобразовании времени содержатся следы от преобразований Лоренца, но они второго порядка по отношению ${\displaystyle v\over\displaystyle c}$. Таким образом, преобразования Лоренца сводятся к преобразованиям Галилея. Поэтому в пределе малых (по сравнению со скоростью света) скоростей зависимость координаты $Ox$ от времени $\tau$ приобретает вид преобразования типа сдвига, время становится внешним параметром по отношению к преобразованиям трехмерных координат. Время становиться неизменным, внешнее влияние на этот параметр отсутствует.

2.1.2 Интервал собственного времени

Рассмотрим покоящуюся систему отсчета $K$. Рассмотрим в ней два события, скажем, колебание математического маятника, покоющегося относительно этой системы. Первое событие - прохождение маятника через точку равновесия, а второе - его повторное прохождение через равновесную точку. Пространственное расстояние между двумя событиями равно нулю $dx=0$, $dy=0$, $dz=0$. Тогда интервал между двумя этими событиями определяет интервал собственного времени $ds^2=c^2d\tau^2$.

Это определение принятое в специальной теории относительности остается справедливым и в общей теории относительности.

Рассмотрим теперь зависимость интервалов времени и длины от состояния движения. Пусть в системе $\hat K$ покоятся часы. Рассмотрим два события в системе $\hat K$. Первое событие - показание часов $\hat t_0=0$ в точке $\hat x=0$, $\hat y=0$, $\hat z=0$. Второе событие - показание часов $\hat t_1=1$ сек в той же точке пространства. Время в системе координат $\hat K$ между этими событиями есть $\tau =t_1- t_0=1$ сек. Интервал между этими событиями есть $ds=cd\tau=3\cdot 10^{10}$ см/сек $\times 1$ сек=300 000 км. Найдем время, которое прошло между этими событиями в системе $K$, в которой покоится наблюдатель измеренное по часом этого наблюдателя. Преобразование времени из системы $\hat K$ в систему $K$ осуществляется по формуле:

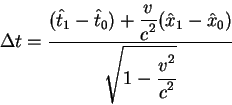
\begin{displaymath} \Delta t={\displaystyle(\hat t_1 -\hat t_0) +{\displaystyle ... ...splaystyle\sqrt{1-{\displaystyle v^2\over\displaystyle c^2}}} \end{displaymath}

поскольку пространственное расстояние в системе $\hat K$ между двумя событиями равно нулю, а интервал времени равен $\Delta \hat t=1$ сек, то в системе $K$ часы покажут, что прошло время:

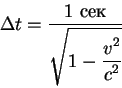
\begin{displaymath} \Delta t={\displaystyle\mbox{1 сек}\over\displaystyle\sqrt{1-{\displaystyle v^2\over\displaystyle c^2}}} \end{displaymath}

Итак, для наблюдателя, который покоится в системе координат $K$ часы показывают, что прошло больше времени, чем 1 сек. Это один из самых неожиданных выводов специальной теории относительности. Для неспециалистов этот вывод представлялся парадоксальным и послужил одним из поводов для попыток теоретически опровергнуть специальную теорию относительности, доказать ее внутреннюю противоречивость.

Одним из наиболее распространенных способов опровергнуть СТО служил т.н. парадокс близнецов. Он формулировался следущим образом.

Рассмотрим двух братьев - близнецов. Один из них улетает на ракете в длительное путешествие. Ракета двигается со скоростью близкой к скорости света, так что $\sqrt{1-{\displaystyle v^2\over\displaystyle c^2}}=0.1$ Второй остается на Земле. Первый брат после путешествия возвращается на Землю. Его собственные часы показывают, что прошло, скажем, один год. Часы второго брата показывают, что прошло 10 лет. Вывод: брат - близнец живщий на Земле постарел на 10 лет, в то время как его брат - путешественник постарел только на один год.

"Хорошо" - говорит желающий опровергнуть СТО. "Теперь давайте рассмотрим ситуацию с точки зрения брата - путешественника. С его точки зрения Земля движется со скоростью близкой к скорости света, а следовательно, на Земле часы должны идти медленнее. Брат - путешественник, вернувшись на Землю обнаружит, что у его брата - близнеца часы показывают только 365 дней."
"Парадокс!"
восклицает опровергатель,
"Это доказывает внутреннюю противоречивость СТО!"
После чего делается вывод, что СТО не верна.

Разумеется, этот вывод основан на ошибке. Ошибка заключается в том, что космонавт, путешествующий на ракете, часть пути находится в неинерциальной системе отсчета. Поэтому две системы неэквивалентны. Доказано это будет, когда мы познакомимся с вычислением собственного времени в ускоренных системах отсчета. Пока же ограничимся указанием на то, что брат - близнец оставшийся на Земле, постареет больше чем путешественник.

2.1.3 Длина движущегося стержня

Рассмотрим теперь как меняются собственные длины стержней в движущейся и покоющейся системах отсчета.

Для этого выпишем преобразование пространственной координаты (2.9) из движущейся в неподвижную систему:

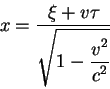\begin{displaymath} x={\displaystyle\xi +v\tau\over\displaystyle\sqrt{1-{\displaystyle v^2\over\displaystyle c^2}}} \end{displaymath} (2.13)

Размер стержня в неподвижной системе обозначим $x_1- x_0=l_p$. В покоящейся системе отсчета его размер определяется выражением:

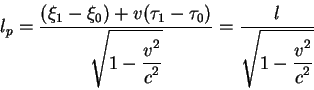\begin{displaymath} l_p={\displaystyle(\xi_1 -\xi_0) +v(\tau_1-\tau_0)\over\disp... ...isplaystyle\sqrt{1-{\displaystyle v^2\over\displaystyle c^2}}} \end{displaymath} (2.14)

поскольку размер стержня в движущейся системе $l$ необходимо определять в один и тот же момент времени $\tau_1=\tau_0$. Поэтому длина стержня будет максимальна в той системе отсчета в которой стержень покоится. В любой другой инерциальной системе отсчета, которая движется относительно покоящейся со скоростью $v$ длина стержня будет меньше:
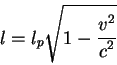\begin{displaymath} l=l_p \sqrt{1-{\displaystyle v^2\over\displaystyle c^2}} \end{displaymath} (2.15)

Пусть стержень длиной $l$ в собственной системе отсчета движется со скоростью $v$ относительно фотоаппарата далекого наблюдателя. За стержнем параллельно ему расположена линейка с нанесенными метками длины, которая покоится относительно наблюдателя. Направление на фотоаппарат составляет угол $\theta$ с направлением скорости стержня. Чему равна кажущаяся длина стержня? Какая часть мерной линейки закрыта стержнем?

2.2 Общие преобразования системы координат, бусты.

Рассмотрим теперь общие преобразования систем координат, которые включают в себя не только четырехмерные повороты связывающие ось времени и одну из пространственных осей, но также и трехмерные вращения. Такие общие преобразования позволяют сделать редукцию на момент наблюдений.

Как и в параграфе посвященном обсуждению вращений рассмотрим линейное преобразование типа:

\begin{displaymath} \hat x^{\alpha}=\sum_{\beta} \Omega^{\alpha}_{\beta} x_{\beta}, \end{displaymath} (2.16)

где $x_{\alpha}$ -координаты вектора в системе $K$, $\hat x_{\alpha}$ координаты того же вектора в системе $\hat K$. Матрица $\Omega_{\alpha \beta}$ определяет вращение. Будем обозначать вращение иногда буквой $\hat \Omega$, той же, что и матрицу. Кроме того, теперь координаты нумеруются буквами греческого алфавита и пробегают значения $\alpha \ni (0, 1, 2, 3)$. Всюду ниже будем придерживаться этого правила. Греческие буквы будут нумеровать четыре координаты (одну временную 0 и три пространственных 1, 2, 3), латинские (кроме специально оговоренных случаев) три пространственные координаты. В связи с этим греческие индексы будем иногда именовать пространственно - временнными, а латинские - пространственными индексами.

Напишем несколько дополнительных условий на вращение. Теперь преобразования такого типа должны оставлять инвариантной четырех форму вида:

\begin{displaymath} S^2=x_0^2 - x_1^2 -x_2^2 -x_3^2 \end{displaymath} (2.17)

тогда такие преобразования называются преобразованиями Лоренца. Введем матрицу:

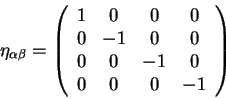\begin{displaymath} \eta_{\alpha \beta}= \left( \begin{array}{cccc} 1& 0& 0& 0 \... ...1& 0& 0 \\ 0& 0& -1& 0 \\ 0& 0& 0& -1 \\ \end{array}\right) \end{displaymath} (2.18)

при преобразованиях Лоренца имеет место равество

\begin{displaymath} \hat \Omega^* \hat \eta \hat \Omega=\hat \eta \end{displaymath}

здесь $\hat \Omega^*$ означает транспонированную матрицу. Отсюда легко заключить, что $Det(\eta)=\pm 1$, следовательно существует обратное преобразование $\hat \eta^{-1}$, которое также является преобразованием Лоренца. Произведение двух преобразований Лоренца также дает преобразование Лоренца, поэтому преобразования Лоренца образуют группу. Уравнение $S^2=x_0^2 - x_1^2 -x_2^2 -x_3^2 $ определяет в четырехмерном пространстве конус (его называют световым конусом). Световой конус делит все пространство - время на две внутренние полы конуса, в которых $S^2>0$ и внешние области, в которых $S^2<0$.

Пусть $\hat \omega$ - матрица преобразования (вращение) трехмерного пространства. Рассмотрим преобразование в четырехмерном пространстве вида:

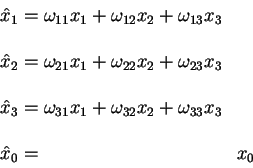
\begin{displaymath} \begin{array}{l} \hat x_1=\omega_{11}x_1 +\omega_{12}x_2 +\o... ...mega_{31}x_1 +\omega_{32}x_2 +\omega_{33}x_3 +} x_0 \end{array}\end{displaymath}

Это преобразование принадлежит группе преобразований Лоренца. Оно оставляет без изменения координату $x_0$ в сумме (2.17) и не меняет сумму $x_1^2 +x_2^2 +x_3^2$. Поскольку с каждым таким преобразованием можно отождествить вращение, то легко видеть, что трехмерные вращения образуют подгруппу преобразований Лоренца.

Напишем матрицу поворота с учетом четвертой координаты:


\begin{displaymath} \hat \Omega= \left( \begin{array}{llll} \omega_{11} & \omega... ... & \omega_{33} & 0 \\ 0 & 0 & 0 & 1 \\ \end{array} \right) \end{displaymath} (2.19)

Здесь в качестве элементов матрицы четырехмерных поворотов $\hat \Omega$ использованы элементы матрицы трехмерных поворотов $\hat \omega$.

Рассмотрим теперь четырехмерные линейные преобразования типа (2.16). Отметим, что такие линейные преобразования являются преобразованиями типа вращения, но не преобразованиями типа сдвига. Для начала найдем преобразование связанное с вращением временной координаты.

Преобразования связанные с преобразованиями Лоренца включающими временную координату, но исключающие вращения пространственных координат математики называют преобразованиями гиперболического поворота, а физики бустами, т.е. преобразованиями меняющими скорость системы координат.

Рассмотрим преобразование в плоскости $(x_3, x_0)$. Такое преобразование не должно менять форму $x_0^2 -x_3^2$. Именно это преобразование математики называют иногда гиперболическим поворотом. Матрицу гиперболического поворота можно записать аналогично матрицам обычного поворота, заменив тригонометрическое косинус и синус на гиперболические косинус и синус:


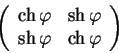
\begin{displaymath} \left( \begin{array}{ccc} \ch \varphi & \sh \varphi \\ \sh \varphi & \ch \varphi \\ \end{array}\right) \end{displaymath}

В четырехмерном виде эта матрица будет иметь вид


\begin{displaymath} \hat \Omega_{03}= \left( \begin{array}{llll} 1 & 0 & 0 & 0 ... ...\ 0 & 0 & \sh \varphi & \ch \varphi \\ \end{array} \right) \end{displaymath} (2.20)

Подобным же образом будут выглядеть матрицы, которые описывают повороты в плоскостях $(x_1, x_0)$, $(x_2, x_0)$. Матрицу сложного поворота, описываемую как тригонометрическими функциями, так и включающую гиперболический поворот, описываемый гиперболическими функциями можно получить пользуясь теоремами сложения тригонометрических и гиперболических функций.

Тем не менее в астрономии проще использовать преобразования Лоренца найденные в другом виде, который мы сейчас обсудим.

Рассмотрим вновь общие преобразования Лоренца вида (2.16), но записанные для дифференциалов координат. Пусть система $\Xi$ покоится относительно наблюдателя, а система $K$ движется относительно него с произвольной скоростью $\vec v$.

Преобразования описываются уравнением:

\begin{displaymath} d\hat x^{\alpha}=\sum_{\beta} \Omega^{\alpha}_{ \beta} d\xi_{\beta}, \end{displaymath} (2.21)

У наблюдателя сопутствующего системе $\Xi$ меняется только время, которое является собственным временем этого наблюдателя. Дифференциалы пространственных координат этого наблюдателя в системе $\Xi$ равны нулю, поскольку координаты неизменны. Поэтому вектор описывающий изменение дифференциалов наблюдателя есть $(d\tau, 0, 0, 0)$. В системе $K$ дифференциалы наблюдателя есть:

$\displaystyle d\hat x^i= \Lambda^i_0 d\tau,$ (2.22)
$\displaystyle \qquad$ (2.23)
$\displaystyle d t = \Lambda^0_0 d \tau . \nonumber$  

Отношение ${\displaystyle d x^i\over\displaystyle d t}=\vec v$ определяет скорость движения координатных систем друг относительно друга. Поэтому можно записать равенство:

\begin{displaymath} \Lambda^i_0= {\displaystyle v^i\over\displaystyle c} \Lambda^0_0 \end{displaymath} (2.24)

Напомним, что $x^0=ct$. Выведем второе уравнение для связи $\Lambda^i_0$ и $\Lambda^0_0$. Для этого вычислим интервал между событиями разделяемыми дифференциалами $d\xi^{\alpha}$ в системе $\Xi$ и дифференциалами $d x^{\alpha}$ в системе $K$. Тогда можно записать уравнение вида:

\begin{displaymath} \sum_{\alpha \beta} \eta_{\alpha \beta} d x^{\alpha} d x^{\b... ...eta} \eta_{\alpha \beta} \Lambda^{\alpha}_0 \Lambda^{\beta}_0 \end{displaymath} (2.25)

Отсюда легко найти (поскольку в системе сопутствующей наблюдателю справедливо равенство $ds^2=c^2d\tau^2$), что:

\begin{displaymath} 1 +\sum_i (\Lambda^i_0)^2 = (\Lambda^0_0)^2 \end{displaymath} (2.26)

Теперь подставляем в уравнение (2.26) уравнение определяющие различные элементы матрицы буста через скорости (2.24) и получаем уравнения для определения элементов матрицы $\hat \Omega$:

$\displaystyle \Lambda^0_0=\gamma,$ (2.27)
$\displaystyle \vphantom{\Omega^0_0=\gamma}$  
$\displaystyle \Lambda^i_0={\displaystyle v^i\over\displaystyle c} \gamma,$  

где $\gamma={\displaystyle 1\over\displaystyle\sqrt{1-{\displaystyle v^2\over\displaystyle c^2}}}$.

Уравнения (2.25, 2.26) являются следствием более общего уравнения:

\begin{displaymath} \eta_{\mu \nu}=\sum_{\alpha \beta} \Lambda^{\alpha}_{\mu} \Lambda^{\beta}_{\nu} \eta_{\alpha \beta} \end{displaymath} (2.28)

Пользуясь этим уравнение можно найти элементы матрицы $\hat \Omega$ с двумя пространственными индексами. Следует, однако, сразу сказать, что элементы этой матрицы определяются неоднозначно. Они всегда могут быть умножены на матрицу трехмерного вращения.

Выберем вид трехмерных элементов четырехмерной матрицы вращения как:

\begin{displaymath} \Lambda^i_j=\delta^i_j -v^i v_j {\displaystyle\gamma -1\over\displaystyle v^2} \end{displaymath} (2.29)

Заметим, что векторные компоненты с нижними индексами отличаются знаком от векторных компонент с верхними индексами $v_j=\eta_{j i}v^i$.

Произвольное преобразование Лоренца может быть выражено как произведение трехмерного вращения с бустом, который описывается матрицей $\Lambda^{\mu}_{\nu}$. Доказательство этого утверждения выходит за рамки курса, но читатель, знакомый с теорией групп легко воспроизведет его. Представим произвольное преобразование Лоренца в виде:

\begin{displaymath} \Omega^{\mu}_{\nu}=\Lambda^{\mu}_{\alpha}\omega^{\alpha}_{\nu} \end{displaymath} (2.30)

В таком виде преобразования Лоренца легко применять для получения уравнений редукции.

2.3 Преобразования векторов

Из курса линейной алгебры известно, что при преобразованиях вида (2.21) вектора преобразуются как

\begin{displaymath} A^{\mu}=\Omega^{\mu}_{\nu} A^{\nu} \end{displaymath} (2.31)

Кроме этого, общего, уравнения можно также привести еще несколько уравнений, которые являются очень полезными при выводе уравнений редукции, хотя они обладают меньшей общностью, чем (2.31). Одним из таких уранений является скалярное произведение векторов. Скалярное произведение двух векторов:

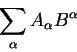
\begin{displaymath} \sum_{\alpha} A_{\alpha}B^{\alpha} \end{displaymath}

является инвариантом координатных преобразований. Докажем это для линейных преобразований вида (2.21). Пусть вектора $A_{\alpha}$ и $B^{\alpha}$ заданы в системе $\Xi$, сделаем преобразование вида (2.21) к новой системе координат $K$, которая движется со скоростью $\vec v$ относительно системы $\Xi$, кроме того, оси системы $K$ повернуты относительно первой системы в произвольном направлении, которое характеризуется тремя углами Эйлера. Теперь вычислим компоненты векторов $A_{\alpha}$ и $B^{\alpha}$ в новой системе $K$:

\begin{displaymath} \hat A_{\mu}=\Omega_{\mu}^{\alpha} A_{\alpha}, \end{displaymath}

и


\begin{displaymath} \hat B^{\mu}=\Omega^{\mu}_{\alpha} B^{\alpha} \end{displaymath}

Скалярное произведение векторов в системе $K$ выражается через произведение векторов в системе $\Xi$ с матрицами преобразования:

\begin{displaymath} \hat A_{\alpha} \hat B^{\alpha}= \Omega_{\alpha}^{\beta}\Omega_{\gamma}^{\alpha} A_{\beta} B^{\gamma} \end{displaymath}

Прямым вычисление произведения мариц можно показать, что

\begin{displaymath} \Omega_{\alpha}^{\beta}\Omega_{\gamma}^{\alpha} =\delta^{\beta}_{\gamma} \end{displaymath} (2.32)

Здесь $\delta^{\alpha}_{\beta}$ - символ Кронекера или единичная матрица2.2:


\begin{displaymath} \delta^{\alpha}_{\beta}= \left( \begin{array}{cccc} 1& 0& 0&... ...& 1& 0& 0 \\ 0& 0& 1& 0 \\ 0& 0& 0& 1 \\ \end{array}\right) \end{displaymath} (2.33)

Подставим (2.33) в (2.32) и полчим, что скалярное произведение векторов в двух системах координат равно друг другу. Это и означает, что скалярное произведение является инвариантом при преобразованиях Лоренца. Заметим сразу, что скалярное произведение является инвариантным при любых, даже нелинейных преобразованиях. Доказательство этого утверждения отложим до пятой лекции.

Кроме векторов нам иногда придется производит вычисления с объектами более сложной природы - тензорами и тензорными плотностями.

Тензор второго ранга эквивалентен четырехмерной квадратной матрице $A^{\alpha \beta}$. Этот тензор преобразуется согласно правилу:

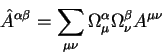
\begin{displaymath} \hat A^{\alpha \beta} =\sum_{\mu \nu} \Omega^{\alpha}_{\mu} \Omega^{\beta}_{\nu} A^{\mu \nu} \end{displaymath}

в случае, когда надо преобразовать тензоры второго ранга с двумя нижними индексами или с одним верхним и одним нижнем индексами необходимосуммировать их с $\hat \Omega$ матрицами с двумя верхними индексами суммирования или со смешанными индексами суммирования.

Тензоры более высокого ранга при преобразованиях содержать больше произведений матриц $\hat \Omega$. тензоры третьего ранга три матрицы, тензоры четвертого ранга - четыре и т.п.

2.4 Четырехмерная скорость

Кинематические и динамические величины в четырехмерном пространстве отличаются от соответствующих трехмерных величин. Вначале определим четырехмерную скорость.

Обычная трехмерная скорость определяется как отношение пройденного пути на промежуток времени, за который этот путь пройден:

\begin{displaymath} \vec v={\displaystyle d \vec r\over\displaystyle dt} \end{displaymath}

Из этой формулы видно, что для определения скорости в трехмерном пространстве используется внешний по отношению трехмерному пространству параметр - время. Если мы построим траекторию пробной частицы в трехмерном пространстве в виде трех функций времени, которые есть:


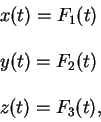
\begin{displaymath} \begin{array}{l} x(t)=F_1(t)\\ \qquad\\ y(t)=F_2(t)\\ \qquad\\ z(t)=F_3(t), \end{array}\end{displaymath}

то скорость можно определить также как касательный вектор

\begin{displaymath} \vec v =({\displaystyle d x(t)\over\displaystyle dt}, {\disp... ...displaystyle dt}, {\displaystyle d z(t)\over\displaystyle dt}) \end{displaymath}

к этой траектории.

По аналогии с этим определением определяют четырехмерную скорость как вектор, касательный к четырехмерной траектории частицы. В качестве параметра вдоль траектории выбирают некоторый афинный параметр. Для частиц, которые обладают массой и движутся со скоростью меньше чем скорость света в качестве афинного параметра вдоль траектории обычно выбирают интервал:


\begin{displaymath} u^{\mu}={\displaystyle d x^{\mu}\over\displaystyle d s} \end{displaymath} (2.34)

Отметим важное отличие четырехмерной скорости, определенной согласно (2.34) от трехмерной скорости. Абсолютная величина трехмерной скорости является произвольной величиной. Абсолютная величина четырехмерной скорости равна единице.

\begin{displaymath} \sum_{\alpha} u^{\alpha} u_{\alpha}=1 \end{displaymath} (2.35)

В случае, когда мы рассматриваем пробную частицу, которая движется со скоростью света (например, фотон), то в качестве параметра вдоль траектории выбирают другой афинный параметр, например, путь, пройденный фотоном. Четырехмерный интервал вдоль траектории частицы движущейся со скоростью света уже выбирать нельзя, поскольку он равен нулю.

Приведем явный вид четырехмерной скорости через трехмерную:

\begin{displaymath} u^{\mu} =\left( \gamma, \gamma {\displaystyle\vec v\over\displaystyle c}\right) \end{displaymath} (2.36)

Приведем также уравнение для редукции волнового вектора фотона к наблюдателю. Для этого воспользуемся тем свойством, что векторное произведение волнового вектора фотона $k^{\mu}$ и четырехмерной скорости наблюдателя является инвариантной величиной

\begin{displaymath} \sum_{\alpha} k_{\alpha} u^{\alpha} =const \end{displaymath} (2.37)

Инвариантность относительно преобразования системы координат означает, что $const$ не меняет своего значения при переходе от, скажем, покоющейся системы координат, к движущейся. Рассмотрим некоторого наблюдателя $O$ и его четырехмерную скорость $u^{\alpha}_O$. В системе координат сопутствующей наблюдателю вектор скорости принимает значение

\begin{displaymath} u^{\alpha}_O = (1, 0, 0, 0) \end{displaymath}

Соответственно скалрное произведение двух четырехмерных векторов вырождается в произведение двух величин: нулевой компоненты волнового вектора фотона и нулевой компоненты четырехмерной скорости. Поскольку второй сомножитель равен единице, то остается только одна величина $k_0$ компонента волнового вектора фотона. Эта компонента отождествляется с наблюдаемой частотой фотона (или с энергией фотона в системе координат, сопутствующей наблюдателю) $\nu_O$. Таким образом определяется значение $const$, которая стоит в правой части уравнения (2.37).

Значение константы в правой стороне равенства (2.37), разумеется, будет другим для другого объекта. Рассмотрим в качестве другого тела источник фотонов. Вычислим правую часть (2.37) в системе координат, которая сопутствует источнику. Теперь константа в правой стороне равенства будет определять частоту излучения $\nu_E$. Естественно, что величина константы будет уже другая.

Cоставим теперь отношение двух величин. Числитель этого отношения - произведение четырехмерной скорости источника фотонов на волновой вектор фотона. Знаменателем является скалярное произведение четырехмерной скорости наблюдателя в системе координат ему сопутствующей.

\begin{displaymath} 1+z={\displaystyle\sum_{\alpha} k_{\alpha} u^{\alpha}\vert _... ...er\displaystyle\sum_{\alpha} k_{\alpha} u^{\alpha}\vert _O } \end{displaymath} (2.38)

Здесь индекс $O$ означает "наблюдатель", а индекс $E$ означает "излучатель". Величина $z$ обычно называется красным смещением, она пришла в релятивистскую теорию из космологии, в космологии это один из основных параметров, который характеризует источник.

Поскольку справа стоит отношение двух констант, которые мы уже вычислили, то напишем это отношение явно:

\begin{displaymath} {\displaystyle\nu_E\over\displaystyle\nu_O} = 1 +z \end{displaymath} (2.39)

Теперь для того, чтобы вычислить частоту фотона, которую будет измерять наблюдатель, поступим следущим образом. В системе координат, сопутсвующей наблюдателю, волновой вектор фотона имеет компоненты


\begin{displaymath} k_{\mu}= 2 \pi \nu_O\left(1, \vec n \right), \end{displaymath}

здесь $\vec n$ -вектор в направлении излучения фотона. Все величины вычислены в системе координат сопутствующей наблюдателю.

Излучатель имеет четырехмерную скорость

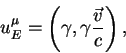
\begin{displaymath} u^{\mu}_E =\left( \gamma, \gamma {\displaystyle\vec v\over\displaystyle c}\right) , \end{displaymath}

где $\vec v$ -трехмерная скорость источника фотонов относительно наблюдателя.

Скалярное произведение в системе координат наблюдателя есть

\begin{displaymath} \sum_{\alpha} k_{\alpha} u^{\alpha}=2 \pi \nu_O \gamma \left( 1 +{\displaystyle(\vec n \vec v)\over\displaystyle c}\right) \end{displaymath} (2.40)

Теперь получаем, что отношение частоты излучателя к частоте того же фотона в системе наблюдателя есть:

\begin{displaymath} {\displaystyle\nu_E\over\displaystyle\nu_O} = \gamma \left( 1 +{\displaystyle(\vec n \vec v)\over\displaystyle c}\right) \end{displaymath} (2.41)

Это есть закон Допплера в специальной теории относительности.

Рассмотрим уравнение (2.41) более подробно.

Будем считать, что источник фотонов и наблюдатель находятся на оси $Ox$ и источник движется вдоль этой оси. Пусть излучатель движется по направлению к наблюдателю. Тогда $(\vec n \vec v)= -v$ и наблюдаемая частоты больше частоты излучателя:

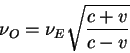
\begin{displaymath} \nu_O = \nu_E \sqrt{{\displaystyle c + v\over\displaystyle c - v}} \end{displaymath}

Частота фотонов смещается в голубую сторону спектра, мы имеем дело с голубым смещением.

В том случае, когда направление распространения фотонов противоположно движению источника $(\vec n \vec v) = v$ возникает эффект красного смещения частоты:

\begin{displaymath} \nu_O = \nu_E \sqrt{{\displaystyle c - v\over\displaystyle c + v}} \end{displaymath}

Рассмотрим еще один любопытный пример. А именно, под каким углом к направлению распространения фотонов должен двигаться источник, чтобы смещение частоты отсутствовало? Итак, на языке математики эту задачу можно сформулировать следущим образом: Найти такое значение $\cos \theta = {\displaystyle(\vec n \vec v)\over\displaystyle v}$ при условии $v \ne 0$, для которого $\nu_O = \nu_E$.

Из условия равенства частот получаем, что косинус угла между направлением движения источника фотонов и направлением на наблюдателя есть:

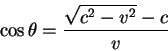
\begin{displaymath} \cos \theta = {\displaystyle\sqrt{c^2 - v^2} - c\over\displaystyle v} \end{displaymath}

Из приведенного уравнения видно, что эффект смещения частоты может отсутствовать лишь для источника удаляющегося от наблюдателя.

Уравнение (2.41) описывает изменение частоты при переходе от движущегося источника к неподвижному наблюдателю. В реальности обычно источник фотонов и наблюдателя разделяет некоторое расстояние. Изменение частоты фотона при рапространении формула (2.41) не описывает. Если в пространстве между источником фотонов и наблюдателем присутствует, например, гравитационное поле, то появляется дополнительное изменение частоты, которое должно быть учтено.


<< 1. Принципы относительности | Оглавление | 3. Ускоренные системы отсчета >>

Публикации с ключевыми словами: Общая теория относительности - специальная теория относительности - системы отсчета - измерение времени
Публикации со словами: Общая теория относительности - специальная теория относительности - системы отсчета - измерение времени
См. также:
Все публикации на ту же тему >>

Мнения читателей [21]
Оценка: 3.1 [голосов: 132]
 
О рейтинге
Версия для печати Распечатать

Астрометрия - Астрономические инструменты - Астрономическое образование - Астрофизика - История астрономии - Космонавтика, исследование космоса - Любительская астрономия - Планеты и Солнечная система - Солнце

Астронет | Научная сеть | ГАИШ МГУ | Поиск по МГУ | О проекте | Авторам

Комментарии, вопросы? Пишите: info@astronet.ru или сюда

Rambler's Top100 Яндекс цитирования