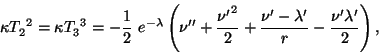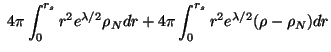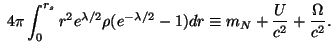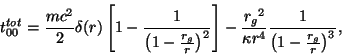- 5.4.1 Проблемы интерпретации шварцшильдова решения
- 5.4.2 Решение методических проблем в рамках полевой формулировки
5.4 Некоторые проблемы интерпретации решений ОТО
Интерпретация решений является одной из важных составляющих частей любой физической теории. Нарликаром [13] были описаны трудности, которые встречаются при описании распределения масс и энергии шварцшильдова решения в обычной геометрической формулировке ОТО. Мы приводим ниже эти аргументы. Затем, в рамках полевой формулировки, показываем, что эти интерпретационные (можно сказать методические) трудности становятся несущественными.
5.4.1 Проблемы интерпретации шварцшильдова решения
Мы представляем проблемы, следуя работе [13].
Выпишем сферически симметричный элемент для статической системы в общем случае:
где
Для выбора постоянной B предполагается, что на пространсвенной бесконечности гравитационные эффекты слабы и делается сравнение с ньютоновым законом тяготения:
Сначала опишем ПЕРВУЮ из проблем рассмотренных в работе [13].
Повторим упражнение предложенное в книге [3],
то есть перепишем уравнение
(5.40) в виде
![$\displaystyle {d \over {dr}}\left [r \left(1 - e^{-\lambda}\right)\right] =
\kappa r^2 c^2 T^{?0}_0 = 8 \pi G r^2 \rho$](http://images.astronet.ru/pubd/2001/09/12/0001170672/img688.gif) |
и проинтегрируем его по объему до поверхности сферического тела с радиусом r = rs:
Такое определение массы не так естественно, как кажется с первого взгляда. Прежде всего, объемный элемент для гиперповерхности t = const в метрике (5.39) не будет больше как в плоском мире
Здесь mN трактуется как нуклонная масса тела, как если бы оно было построено из свободных гравитационно невзаимодействующих частиц с плотностью
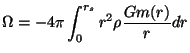 |
и находится в соответствии с ньютоновой потенциальной энергией. Но измененная формула (5.45) также не без изъянов, Бонди, еще в работе [15], отмечал, что член mN не является инвариантным.
ВТОРАЯ проблема рассмотренная Нарликаром [13]
касается проблемы точечной
массы. В ньютоновой гравитации такая проблема решается просто. Сама по
себе она звучит так: Как описывать точечную массу, если мы желаем,
чтобы ньютонов потенциал m/r имел смысл везде, включая точку r =0?
Для этого достаточно предположить, что распределение масс задается в
виде ![]() , где
, где ![]() -функция удовлетворяет обычному
уравнеию Пуассона
-функция удовлетворяет обычному
уравнеию Пуассона
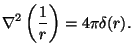 |
Мало того, как при обычном регулярном распределении
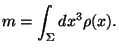 |
Если мы попытаемся в ОТО, используя Шварцшильдово решение,
описать точечную массу, мы встретим концептуальные трудности.
Предположим, что решение (5.43) имеет место во всем
пространстве-времени, включая
мировую линию r=0, тогда материальное распределение
будет описываться компонентами тензора энергии-импульса:
5.4.2 Решение методических проблем в рамках полевой формулировки
Две отмеченные проблемы выглядят как методические, тем не менее они не разрешаются в рамках геометрической формулировки ОТО. Мы их разрешаем с помощью полевого подхода [16].
Для решения (5.39) выберем плоский фон в координатах этого же решения:
Отметим, что если
Интеграл энергии с соответствующим вектором Киллинга (см.
(5.18))
в координатах (5.47) приобретает вид:
где вертикальная черта -- ковариантная производная по пространственной метрике в (5.47). Если есть необходимость, то интегрирование как в (5.49), так и в (5.50) может быть ограничено любой сферой r = r0.
В случае интегрирования внутри материи (5.49), мы делаем
предположение, что распределение достаточно регулярно,
чтобы было допустимо интегрирование.
Чтобы получить значение интеграла масс,
как видно из (5.50),
достаточно знать значения гравитационных потенциалов
(5.48) на границе -- нет необходимости знать явные значения
материальных переменных для вычисления (5.49), достаточно знать
что они удовлетворяют уравнениям Эйнштейна.
Так, для сферически симметричной островной системы интеграл (5.50)
для полной массы дает естественный результат mc2. В
любом случае, уравнение (5.49) решает ПЕРВУЮ методическую
проблему, действительно в (5.49)
мы интегрируем в плоском
пространстве и имеем правильный элемент
интегрирования
![]() .
.
Теперь перейдем ко ВТОРОЙ проблеме -- проблеме точечной массы.
Поле (5.48) в ваккуме
имеет вид:
которая разбивается на материальную и гравитационнуую части:
Формулы (5.52) - (5.54), может быть не так изящно как в ньютоновой гравитации, но вполне разумно (в отличие от геометрической формулировки) представляют плотность массы для точечной частицы в ОТО. Мало того, подстановка плотности энергии ttot00 из (5.52) в интеграл масс (5.49) вполне допустимо и прямое интегрирование дает ожидаемый результат mc2. Таким образом вторая методическая проблема также решается в рамках полевого формализма.
<< 5.3 Интерпретация заданного фона | Оглавление | Литература к Лекции 5 >>
|
Публикации с ключевыми словами:
законы сохранения - Общая теория относительности - гравитация
Публикации со словами: законы сохранения - Общая теория относительности - гравитация | |
См. также:
Все публикации на ту же тему >> | |