<< 7.2 Вырождение вещества | Оглавление | 7.4 Нейтронизация вещества >>
7.3 Предел Чандрасекара и фундаментальная масса звезды.
При увеличении плотности вещества (![]() г/см
г/см![]() ) электроны
становятся релятивистскими, их давление
) электроны
становятся релятивистскими, их давление
![]() , и из уравнения
гидростатического равновесия (см. раздел 5.4.1) находим, что
равновесие возможно только при одной массе (предел Чандрасекара)
, и из уравнения
гидростатического равновесия (см. раздел 5.4.1) находим, что
равновесие возможно только при одной массе (предел Чандрасекара)
Точное значение для релятивистского вырожденного электронного газа
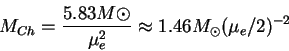
где
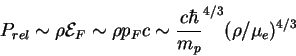
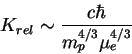
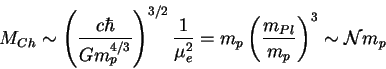
где
Т.о. мы получили фундаментальное число барионов в типичной
звезде
![]() . Полное число барионов внутри сегодняшнего горизонта
событий
. Полное число барионов внутри сегодняшнего горизонта
событий
![]() , где полное
число барионных объектов звездной массы внутри Хаббловского радиуса
, где полное
число барионных объектов звездной массы внутри Хаббловского радиуса
![]() см есть
см есть
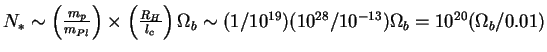 . Если
масса типичной галактики
. Если
масса типичной галактики
![]() , полное число галактик внутри Хаббловского радиуса
, полное число галактик внутри Хаббловского радиуса
![]() , т.е. 1 галактика приходится в среднем
на каждые 30 квадратных секунд неба !
, т.е. 1 галактика приходится в среднем
на каждые 30 квадратных секунд неба !
Если действию гравитации в звезде противостоит давление вырожденных
нейтронов (нейтронная звезда), можно получить аналогичную предельную массу
для нейтронной звезды (иногда ее называют пределом Оппенгеймера-Волкова,
которые в 1939 году рассмотрели строение простейшей нейтронной звезды,
состоящей только из вырожденных нейтронов). В отличие от предела
Чандрасекара, который зависит только от химического состава вещества (этим
определяется число электронов на один нуклон ![]() ), предел
Оппенгеймера-Волкова зависит от точно неизвестного уравнения состояния
материи при ядерных плотностях
), предел
Оппенгеймера-Волкова зависит от точно неизвестного уравнения состояния
материи при ядерных плотностях ![]() г/см
г/см![]() . Для различных уравнений
состояний этот предел находится между
. Для различных уравнений
состояний этот предел находится между
![]() , и его
определение является одной из фундаментальных задач физики нейтронных звезд.
, и его
определение является одной из фундаментальных задач физики нейтронных звезд.
<< 7.2 Вырождение вещества | Оглавление | 7.4 Нейтронизация вещества >>
|
Публикации с ключевыми словами:
звезды - Межзвездная среда - Космология - теоретическая астрофизика - астрофизика
Публикации со словами: звезды - Межзвездная среда - Космология - теоретическая астрофизика - астрофизика | |
См. также:
Все публикации на ту же тему >> | |